[Java] Chapter 9. Tree

✔️ Tree

1. 용어

• 루트(root) : 트리 구조 중 최상위에 존재하는 노드(1을 가리킴)
• 노드(node) : 트리에서 각각의 구성 요소
• 레벨(level) : 트리에서 각각의 층을 나타내는 단어(루트 노드 : 0)
• 형제 노드(sibling) : 같은 레벨의 노드
• 간선(edge) : 노드와 노드를 연결하는 선
• 부모 노드(parent node) : 한 노드를 기준으로 바로 상위에 존재하는 노드
• 자식 노드(child node) : 한 노드를 기준으로 바로 하위에 존재하는 노드
• 높이(heigh) : 트리 중 최고 레벨

2. 순회 방법

• 전위순회(pre-order) : 루트 노드를 먼저 순회한 이후, '왼쪽 하위 -> 오른쪽 하위' 순으로 순회
• 중위순회(in-order) : 왼쪽 가장 하위 노드를 먼저 순회한 이후, '바로 상위 노드 -> 오른쪽 하위' 순으로 순회
• 후위순회(post-order) : 왼쪽 가장 하위 노드를 먼저 순회한 이후, '오른쪽 하위 노드 -> 바로 상위 노드' 순으로 순회
• 레벨순회(level-order) : 레벨 순으로 순회

예시

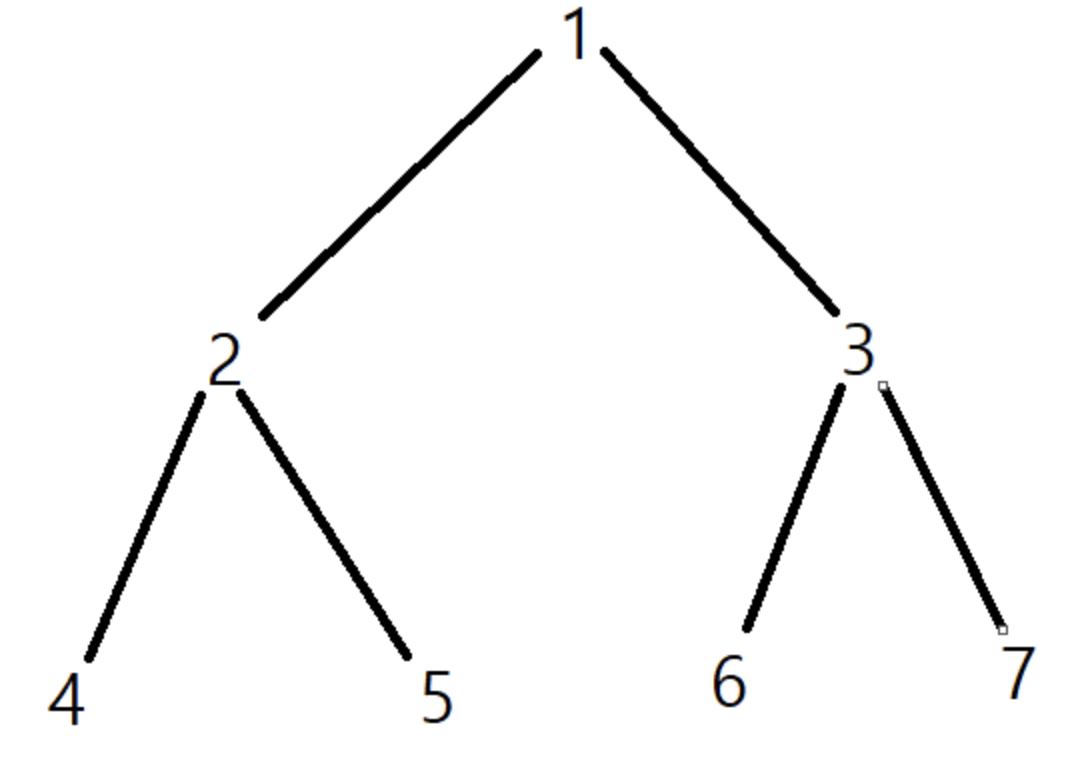
• 전위순회(pre-order) : 1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7
• 중위순회(in-order) : 4 -> 2 -> 5 -> 1 -> 6 -> 3 -> 7
• 후위순회(post-order) : 4 -> 5 -> 2 -> 6 -> 7 -> 3 -> 1
• 레벨순회(level-order) : 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7

3. Node 메서드

메서드	설명
void addLeft(Node node)	현재 노드의 좌측에 노드 연결 정보를 추가함
void addRight(Node node)	현재 노드의 우측에 노드 연결 정보를 추가함
void deleteLeft()	현재 노드의 좌측 노드 연결 정보를 삭제함
void deleteRight()	현재 노드의 좌측 노드 연결 정보를 삭제함

4. Tree 메서드

메서드	설명
Node addNode(Object data)	노드를 새롭게 생성함
void preOrder(Node node)	전위 순회 방법을 이용해 출력함
void inOrder(Node node)	중위 순회 방법을 이용해 출력함
void postOrder(Node node)	후위 순회 방법을 이용해 출력함

예제

Tree.java

package Tree;

public class Tree {
    int cnt;

    public Tree() {
        cnt = 0;
    }
    public class Node {
        Object data;
        Node left;
        Node right;

        public Node(Object data) {
            this.data = data;
            left = null;
            right = null;
        }
        public void addLeft(Node node) {
            left = node;
            cnt++;
        }
        public void addRight(Node node) {
            right = node;
            cnt++;
        }
        public void deleteLeft() {
            left = null;
            cnt--;
        }
        public void deleteRight() {
            right = null;
            cnt--;
        }
    }

    public Node addNode(Object data) {
        Node n = new Node(data);
        return n;
    }
    public void preOrder(Node node) {
        if(node == null) {
            return;
        }
        System.out.print(node.data + " ");
        preOrder(node.left);
        preOrder(node.right);
    }

    public void inOrder(Node node) {
        if(node == null) {
            return;
        }
        inOrder(node.left);
        System.out.print(node.data + " ");
        inOrder(node.right);
    }

    public void postOrder(Node node) {
        if(node == null) {
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.print(node.data + " ");
    }
}

Main.java

package Tree;

import java.util.*;
import Tree.Tree.Node;

public class Main {
    public static void main(String[] args) {
        // 트리 생성
        Tree tree = new Tree();

        // 노드 생성
        Node node1 = tree.addNode(1);
        Node node2 = tree.addNode(2);
        Node node3 = tree.addNode(3);
        Node node4 = tree.addNode(4);
        Node node5 = tree.addNode(5);
        Node node6 = tree.addNode(6);
        Node node7 = tree.addNode(7);

        // 트리 연결관계 생성
        node1.addLeft(node2);
        node1.addRight(node3);
        node2.addLeft(node4);
        node2.addRight(node5);
        node3.addLeft(node6);
        node3.addRight(node7);

        // 순회
        System.out.print("preOrder : ");
        tree.preOrder(node1);
        System.out.println();
        System.out.print("inOrder : ");
        tree.inOrder(node1);
        System.out.println();
        System.out.print("postOrder : ");
        tree.postOrder(node1);
        System.out.println();

        // 삭제
        node2.deleteLeft();
        node3.deleteRight();

        // 순회
        System.out.println();
        System.out.print("preOrder : ");
        tree.preOrder(node1);
        System.out.println();
        System.out.print("inOrder : ");
        tree.inOrder(node1);
        System.out.println();
        System.out.print("postOrder : ");
        tree.postOrder(node1);
        System.out.println();
    }
}

위 내용은 다음 블로그를 참고하였습니다.

---

✔️ Binary Search Tree

• 왼쪽 노드는 부모 노드보다 작을 것
• 오른쪽 노드는 부모 노드보다 클 것

---

✔️ Heap Tree

1. Min Heap Tree

• Root에는 항상 최소값만 있어야 함

2. Max Heap Tree

• Root에는 항상 최대값만 있어야 함

---

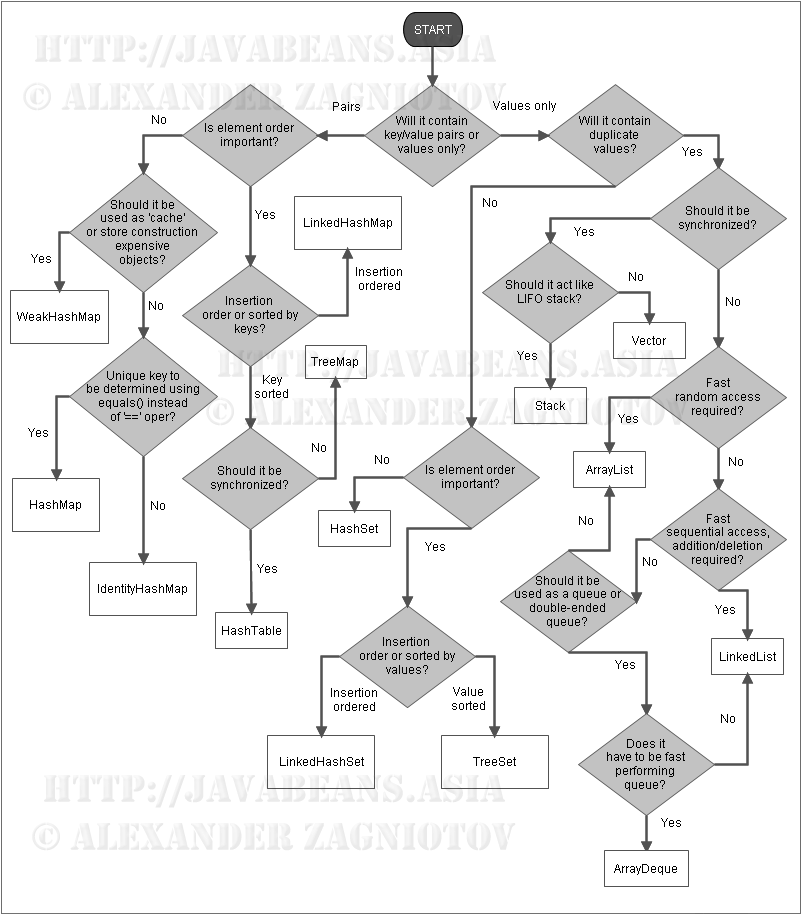
다음은 상황에 따라 사용해야하는 자료구조가 무엇인지 분류해놓은 것이다.