AI/ML/Gradient Boosting
Gradient Boosting Regression 실습(회귀)
위 링크를 참고함
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, ensemble
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_errorboosting기법을 사용하므로 ensemble을 불러와준다.
# Load data
boston = datasets.load_boston()
X, y = shuffle(boston.data, boston.target, random_state=13)
X = X.astype(np.float32)
offset = int(X.shape[0] * 0.9)
X_train, y_train = X[:offset], y[:offset]
X_test, y_test = X[offset:], y[offset:]shuffle 함수로 데이터를 섞고 astype으로 전부 np.float32로 바꿔준다.
그 다음은 train / test를 9:1로 쪼개는 모습. 굳이 이러지 말고model_selection.train_test_split(x, y, ratio) 를 쓰자.
# Fit regression model
params = {'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 2,
'learning_rate': 0.01, 'loss': 'ls'}
clf = ensemble.GradientBoostingRegressor(**params)
clf.fit(X_train, y_train)
mse = mean_squared_error(y_test, clf.predict(X_test))
print("MSE: %.4f" % mse)prams에 hyper-parameter를 정리해 넣어준다. 근데 **params 이게 낯설다. argument를 이런식으로도 넣을 수 있구나
n_estimators: 의사결정나무(weak learner)의 개수
max_depth: 의사결정나무의 최대깊이
min_samples_split: 의사결정나무로 쪼갰을때 leaf node의 최소 데이터량
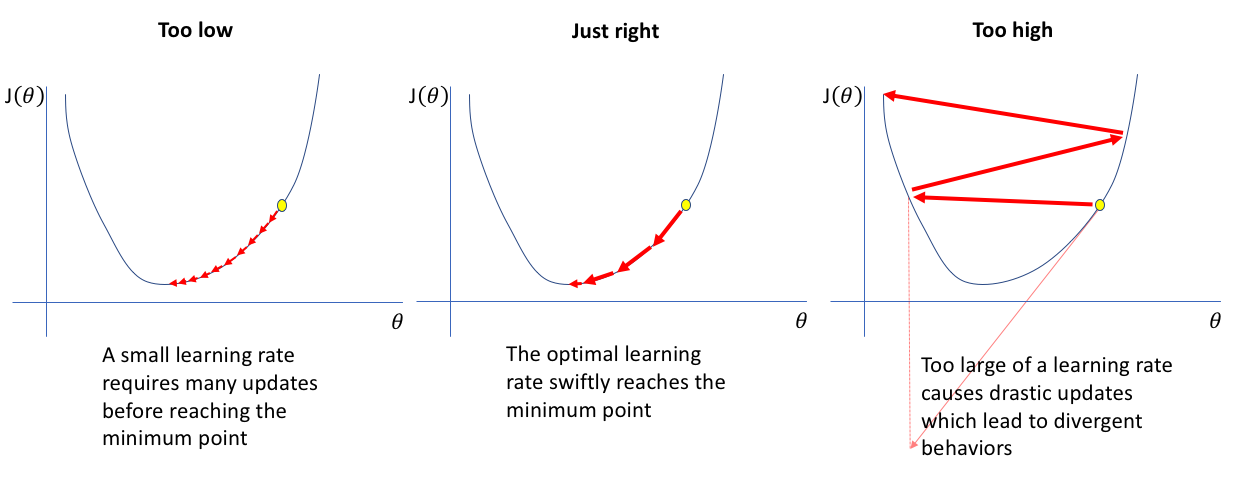
learning_rate: gradient decent 적용시 알파의 값. 작을수록 세밀하게 이동하며 계산량이 많아지고, 너무크면 답이 안나온다. 일반적으로 0.01~0.001사이에서 설정한다.
loss: cost function의 종류를 설정하는것. 위에서 적용한 ls는 최소자승법으로 mse랑 같다.
# Plot training deviance
# compute test set deviance
test_score = np.zeros((params['n_estimators'],), dtype=np.float64)
for i, y_pred in enumerate(clf.staged_predict(X_test)):
test_score[i] = clf.loss_(y_test, y_pred)
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.title('Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, clf.train_score_, 'b-',
label='Training Set Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, test_score, 'r-',
label='Test Set Deviance')
plt.legend(loc='upper right')
plt.xlabel('Boosting Iterations')
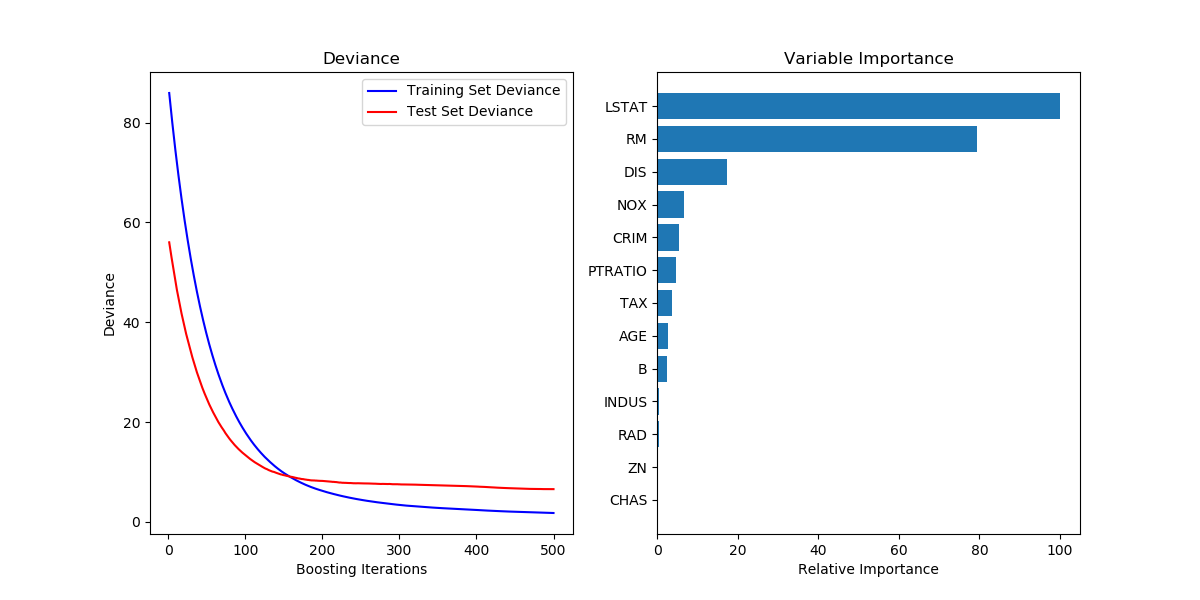
plt.ylabel('Deviance')위 사진의 왼쪽 그림을 만드는 코드이다. 의사결정나무를 몇개 만드냐에 따라 일탈의 정도가 어떻게 변하는지를 보여준다. 사진은 붉은 그래프가 계속 감소하지만 증가한다면 아마 오버피팅일테니 거기서 멈추면 되겠다.
먼저 clf.staged_precit(X_test)는 의사결정나무 1개로 예측한 결과부터 500개까지 만들어 예측한 결과까지 다 담아 iteratable object로 리턴해준다. enumerate는 내용물을 꺼내면서 순서도 같이 꺼내주는 함수이다. 그래서 i에 인덱스를, ypred에 데이터 자체를 꺼내어 test_score에 집어넣는 것이다.
여기서 `clf.loss()` 는 아까 ls를 적어줬으니 MSE를 사용할 것이다.
# Plot feature importance
feature_importance = clf.feature_importances_
# make importances relative to max importance
feature_importance = 100.0 * (feature_importance / feature_importance.max())
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
plt.subplot(1, 2, 2)
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, boston.feature_names[sorted_idx])
plt.xlabel('Relative Importance')
plt.title('Variable Importance')
plt.show()Feature Importances
clf.feature_importances_는 각 열의 중요도를 반환해준다.
Permutation Importances
Feature Importances와 의미는 비슷하지만 계산방식이 다르다고.. 앵간해서는 후자가 더 좋다고함 번외로 LIME이라는 라이브러리도 비슷한 용도로 사용할 수 있다고 한다.
원리는 각 열당 데이터를 무작위로 섞어서 무의미하게 만든다음 모델의 성능이 어떻게 나오는지 보는 것이다. 모델을 매번 수정하는건 비용이 크니 데이터를 수정해서 모델의 성능하락폭을 측정하는 것임.
https://soohee410.github.io/iml_permutation_importance
from sklearn.inspection import permutation_importance
feature_importance = permutation_importance(clf, X_test, y_test, n_repeat=10, random_state=42, n_jobs=2)n_repeat은 섞고 성능측정하는것을 반복하는 횟수이다. n_jobs는 멀티스레드 관련 파라미터.
리턴방식은 2차원 array다.
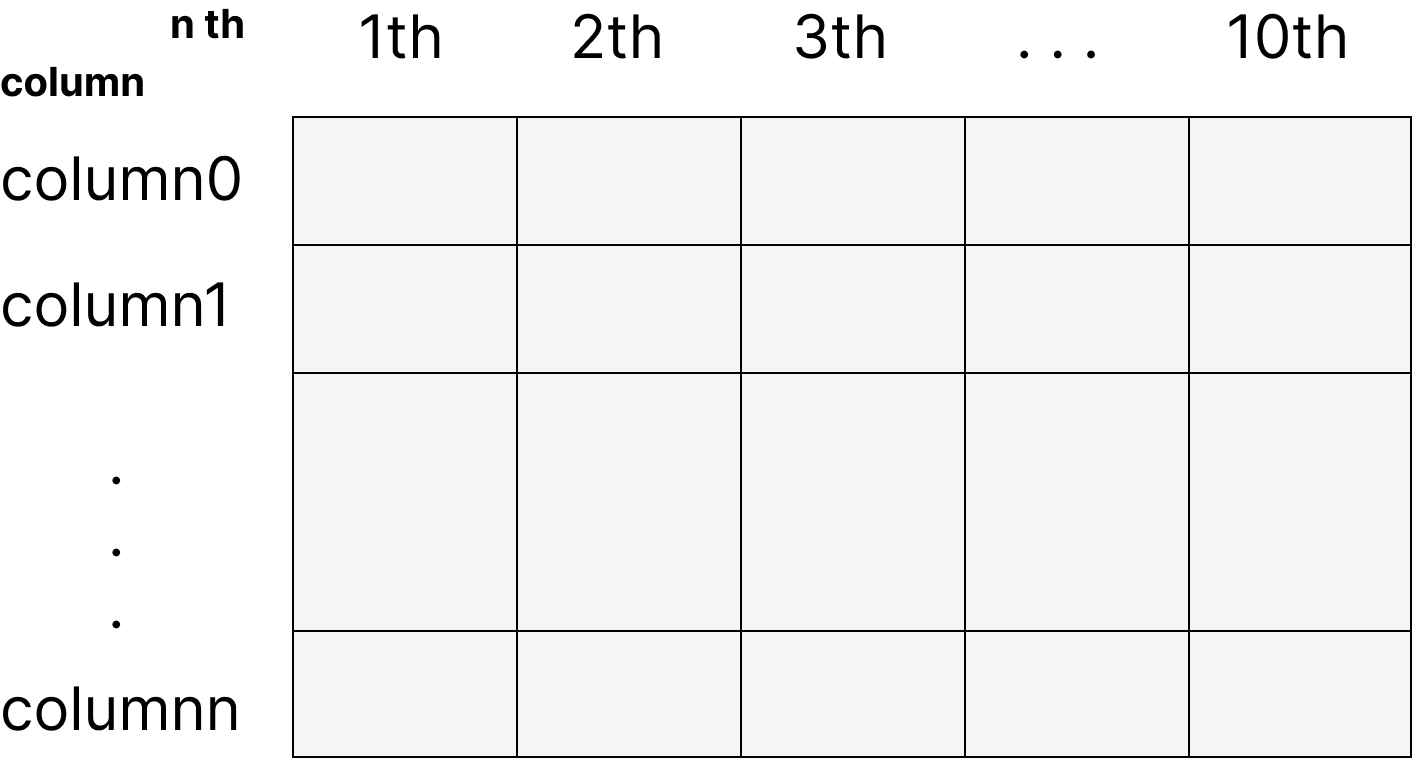
각 행은 기존에 있던 속성을 의미, 열은 시도횟수를 뜻함 데이터는 기존 모델과 성능차이를 의미함. 이를 통해 boxplot 그림도 그릴 수 있다.
절대적인 수치는 원래 성능과 특정 열을 뒤섞었을 때 metric의 차이를 의미한다.
metric은 scoring 이라고 하는 hyper-parameter에 따라 측정되는 지표이다.
scoring을 따로 지정하지 않는 경우(위 코드와 같이) 사용되는 모델의 기본 scorer가 사용된다.
scikit-learn의 모델들은 기본적으로 model.score(x_test, y_test)와 같이 score기능을 제공한다. 회귀분석의 경우 R2 Score(설명계수)를 활용하는데, 0~1사이에서 모델의 설명력을 평가한다. (높을수록 좋음) 분류분석의 경우 보통 Accuracy가 기본 scorer가 된다.
Gradient Boosting Regression 실습(분류)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, ensemble
from sklearn.model_selection import train_test_split
# from sklearn.metrics import mean_squared_error
from sklearn.metrics import accuracy_score분류 문제이므로 mse 대신 accuracy score를 사용한다.
cancer = datasets.load_breast_cancer()
x, y = cancer.data, cancer.target
x_train, y_train, x_test, y_test = train_test_split(x, y, test_size=0.1, random_state=42)
params = {'n_estimators': 1000,
'max_depth': 4,
'min_samples_split': 5,
'learning_rate': 0.01}
clf = ensemble.GradientBoostingClassifier(**params)
clf.fit(x_train, y_train)
acc = accuracy_score(y_test, clf.predict(x_test))
print(acc)GradientBoostingClassifier를 사용한다는 점과 mse 대신 accuracy를 사용한다는 점이 다르다. 여기서 clf.score(x, y)를 사용해도 똑같이 accuracy가 나온다. 그래도 명시적으로 accuracy_score를 사용해주면 덜 헷갈린다.
# Plot training deviance
# compute test set deviance
test_score = np.zeros((params['n_estimators'],), dtype=np.float64)
for i, y_pred in enumerate(clf.staged_predict(X_test)):
test_score[i] = accuracy_score(y_test, y_pred)
plt.figure(figsize=(12, 6))
plt.subplot(1, 1, 1)
plt.title('Accuracy')
plt.plot(np.arange(params['n_estimators']) + 1, clf.train_score_, 'b-',
label='Training Set Deviance')
plt.plot(np.arange(params['n_estimators']) + 1, test_score, 'r-',
label='Test Set Deviance')
plt.legend(loc='upper right')
plt.xlabel('Boosting Iterations')
plt.ylabel('Deviance')test_score[i] 를 accuracy_score로 사용하는 것이 바뀌었다.
외에도 feature importances, roc_curve, auc 등 이전에 배운 것들을 사용할 수 있다.
또 classification report라는 것이 있는데
from sklearn.metrics import classification_report
predictions = clf.predict(x_test)
print(classification_report(y_test, predictions))이렇게 부르면
precision recall f1-score support
class 0 0.50 1.00 0.67 1
class 1 0.00 0.00 0.00 1
class 2 1.00 0.67 0.80 3
accuracy 0.60 5
macro avg 0.50 0.56 0.49 5
weighted avg 0.70 0.60 0.61 5https://scikit-learn.org/stable/modules/generated/sklearn.metrics.classification_report.html
요런 데이터가 나온다.
precision은 각 class라고 예측한 것 들 중 맞아떨어진 비율
recall은 실제 class 인 것들 중 예측에 성공한 것 들의 비율
f1-score는 이 둘의 조화평균
support는 데이터의 개수
macro avg 는 각 열의 평균
weighted avg는 support를 기준으로한 각 열의 가중평균
