힙

우선 순위가 있는 자료를 관리해야 하는데, 죄다 정렬을 하자니 시간복잡도가 올라간다. 반정렬을 통해 시간복잡도와 정렬 모두 잡는다.

모양

이진 트리 구조로 만들어진 정렬된 자료구조이다. root node가 최대 혹은 최솟값을 가지고 느슨한 정렬상태를 보인다.

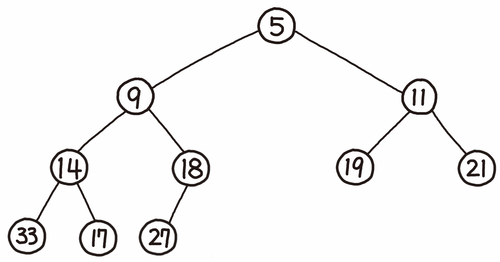
물론 이진트리를 일차원 배열로 구현한다.

이걸 다시 트리로 만들면

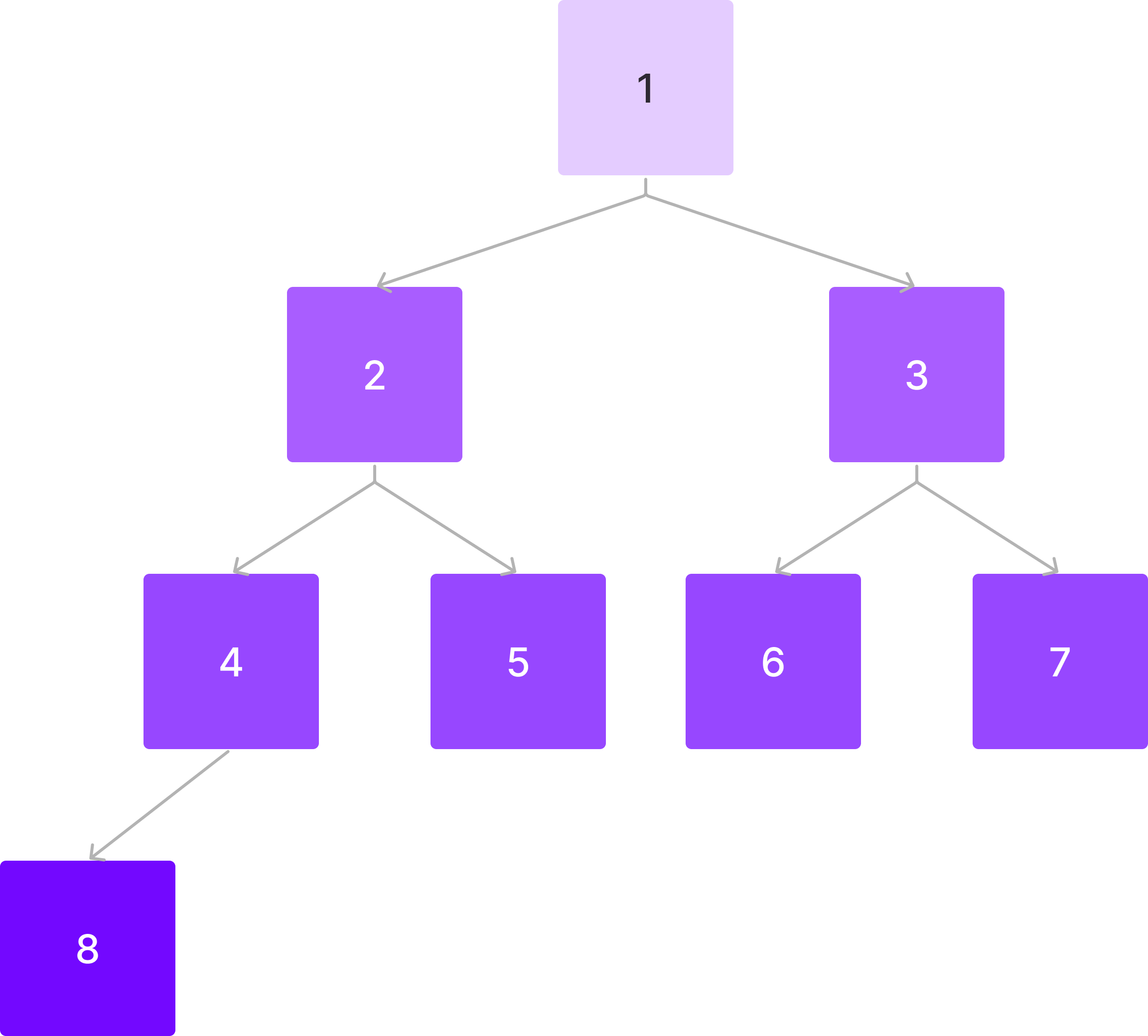
0 인덱스

인덱스0은 사용하지 않는다.
이진트리에서 밑의 자식에 접근하려면
index * 2, index * 2 + 1 이렇게 접근하는게 편한데 root node의 index가 0이라면
(0), (0, 1), (0, 1, 2, 3)
이런식으로 엉망이 된다. 반면 root node = 1이면
(1), (2, 3), (4, 5, 6, 7)
잘 작동할 것이다.

데이터 삽입

rote node가 최댓값이 되는 최대 힙을 기준으로

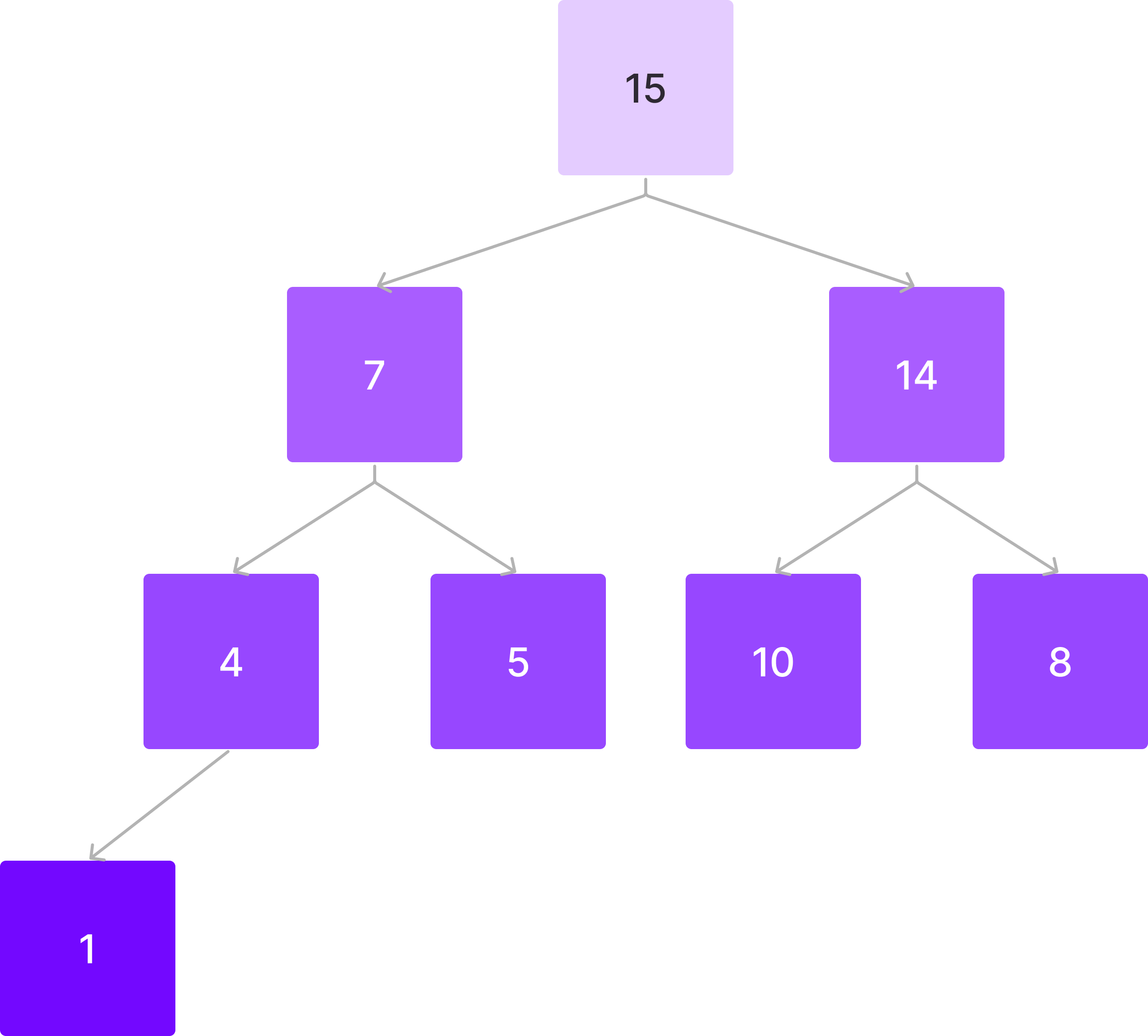
이런 트리가 있다고 하자. 여기서 데이터 11을 삽입한다.

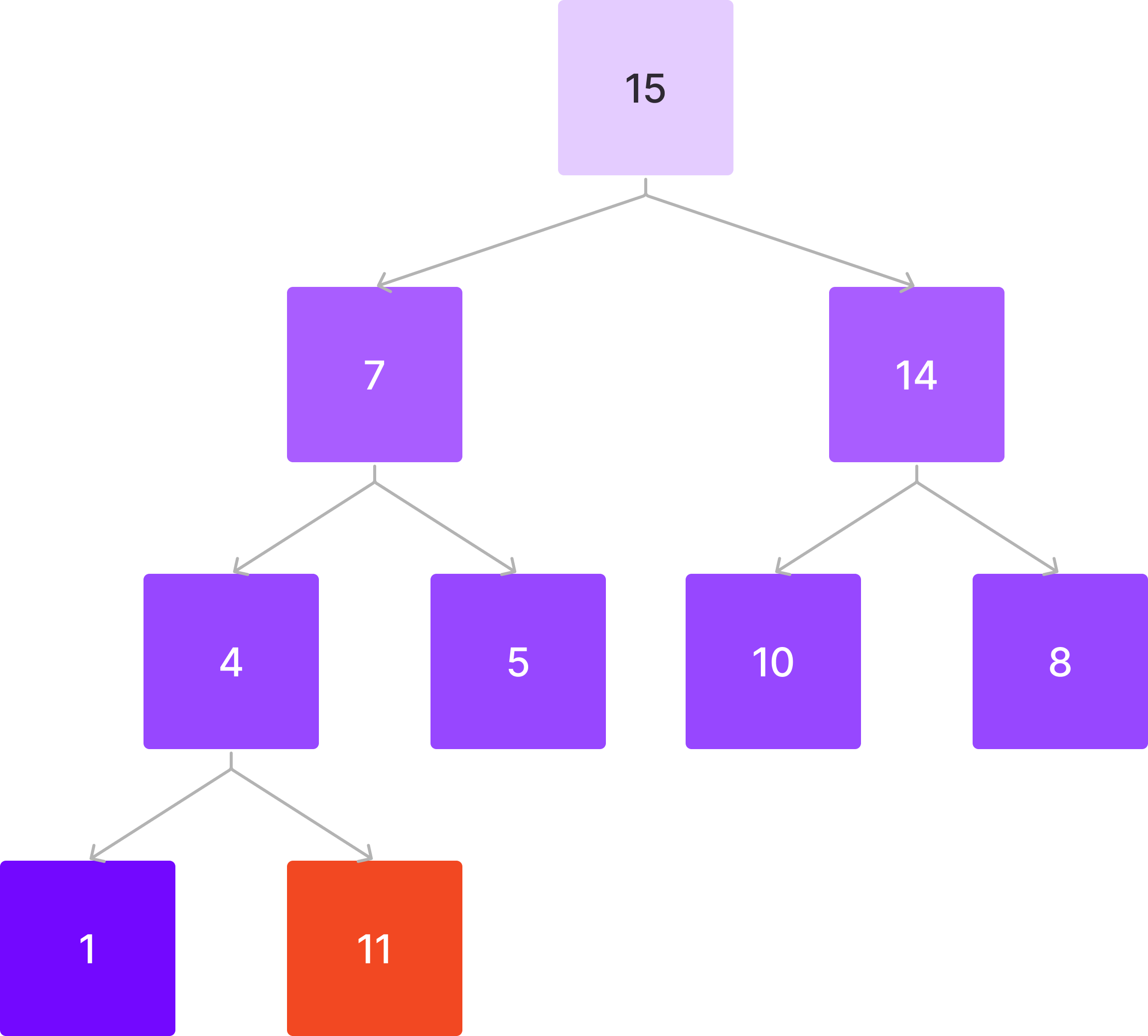
부모 노드와 비교하며 자리를 교환하면 된다.
4 < 11이므로 부모와 자리를 바꾼다.

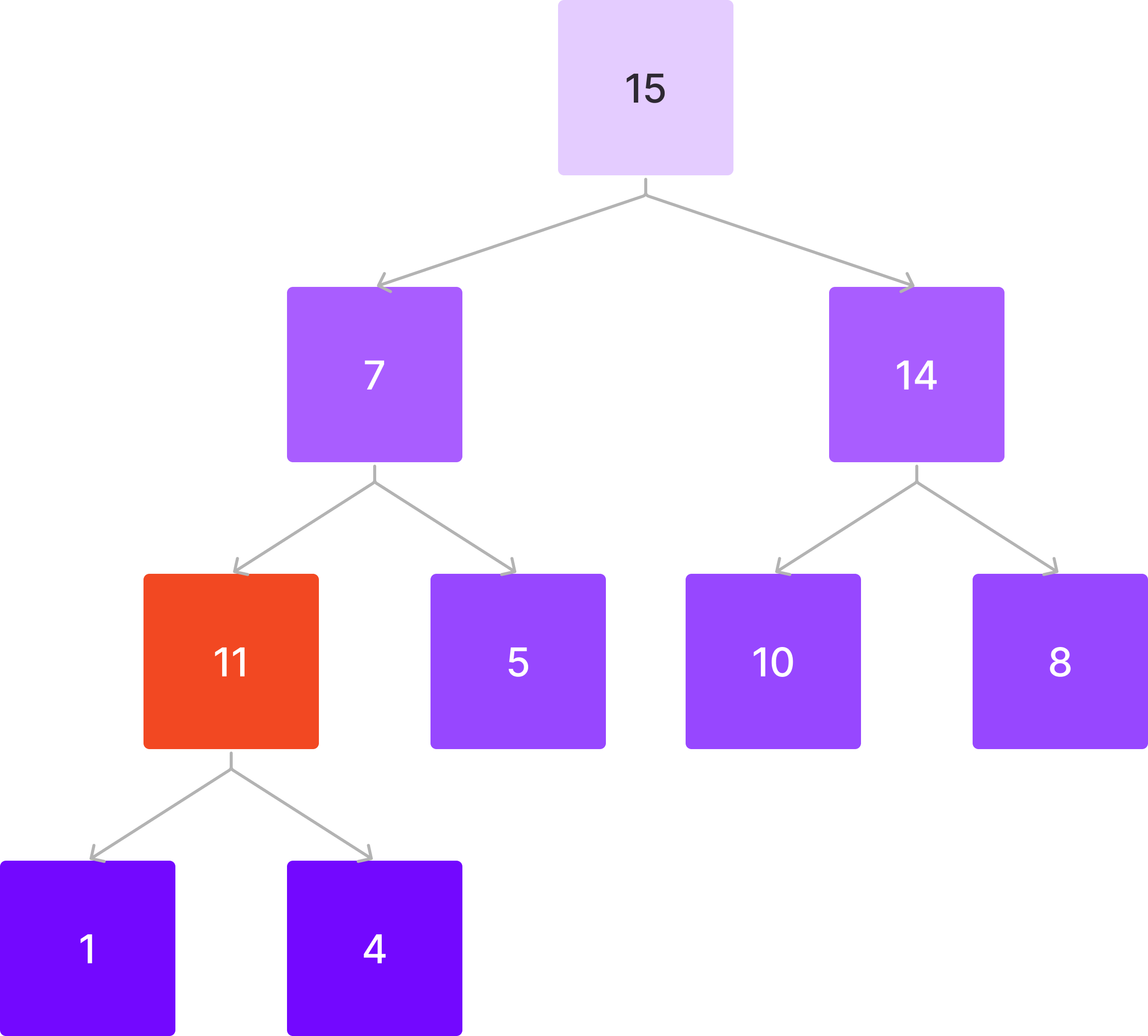
7 < 11이므로 또 부모와 자리를 바꾼다.

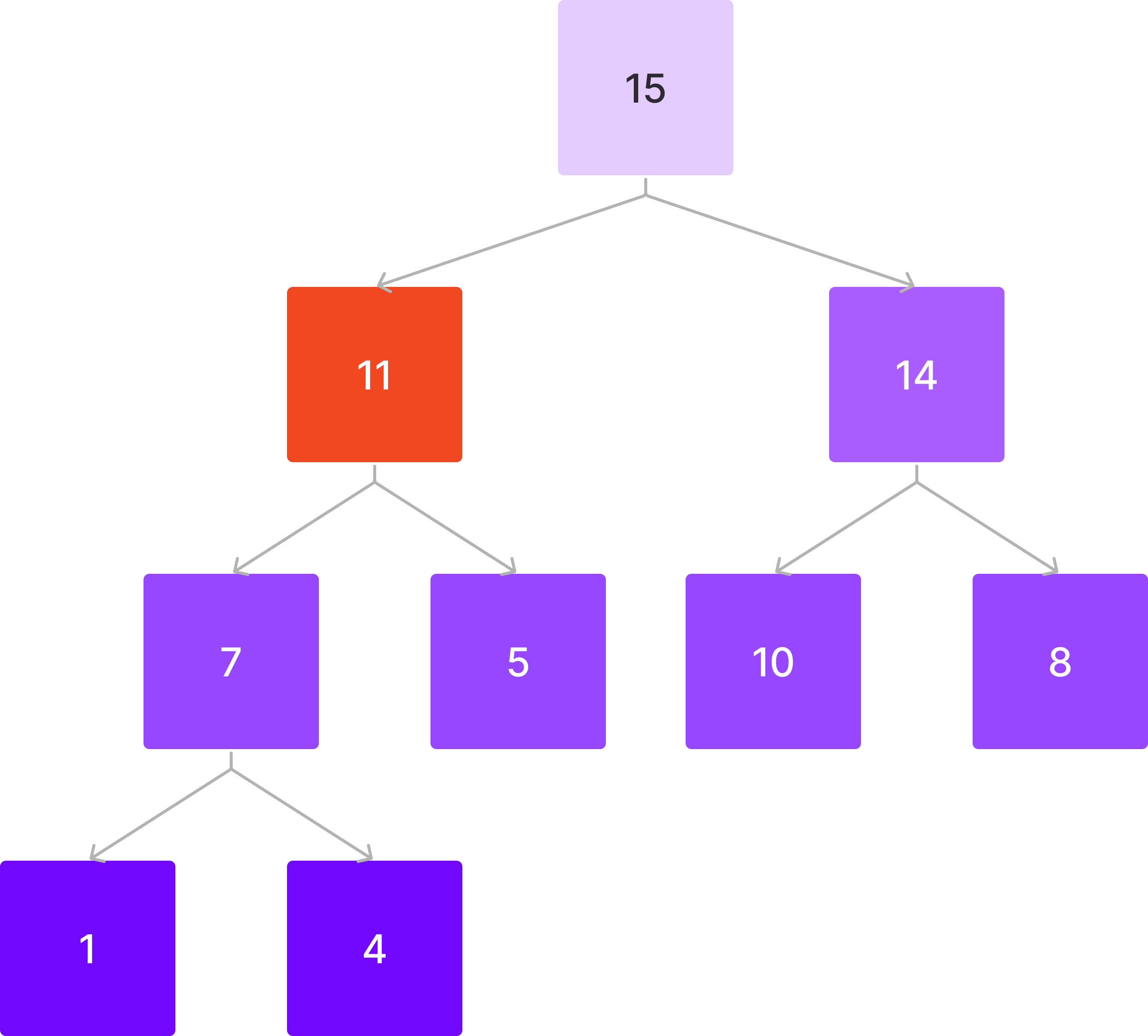
이제 부모보다 작으므로 끝

데이터 삭제

root node만 삭제할 수 있다. 아까의 힙에서 그대로 삭제해보자.

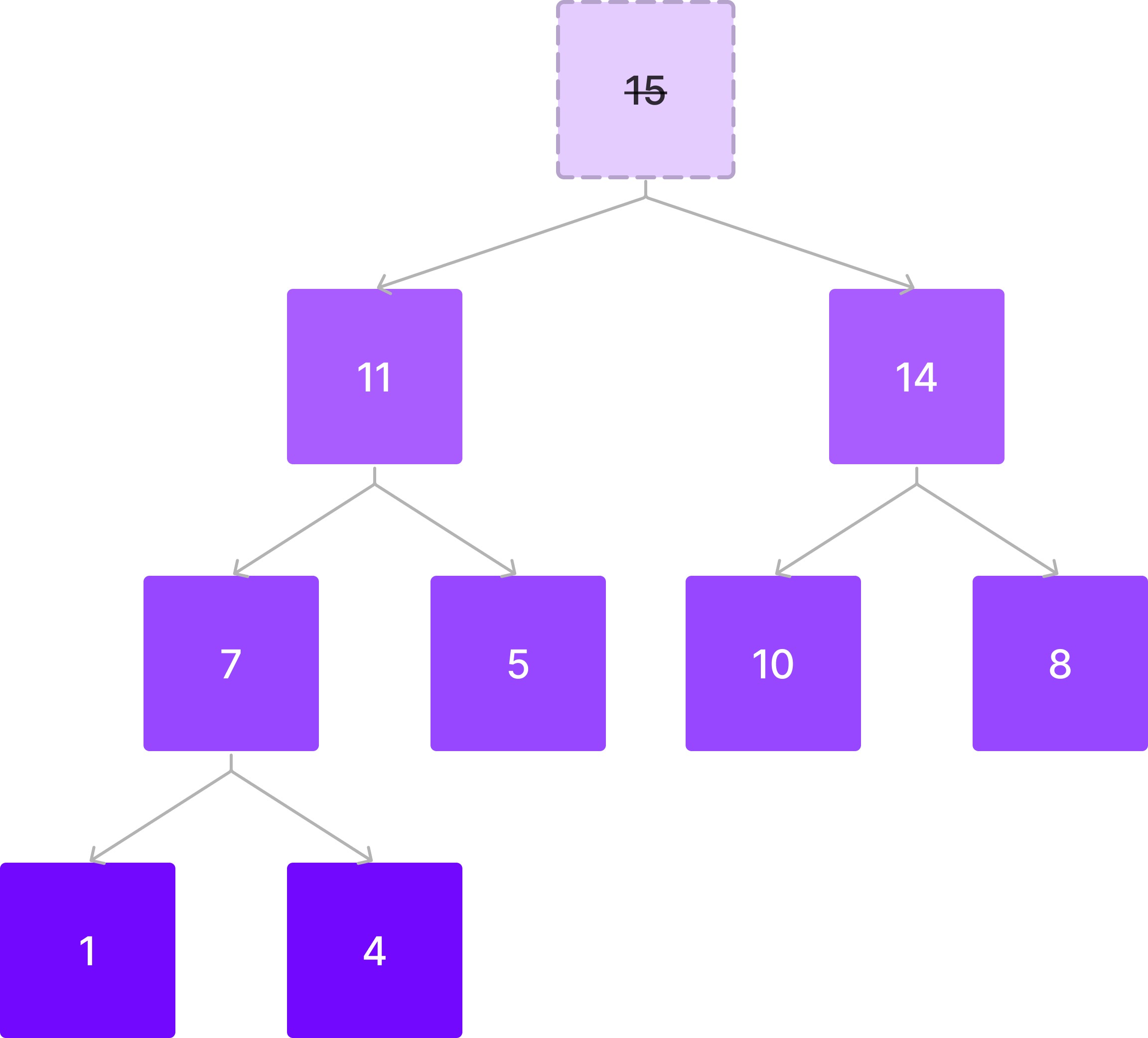
그 다음 마지막 노드를 맨 앞으로 옮긴다.

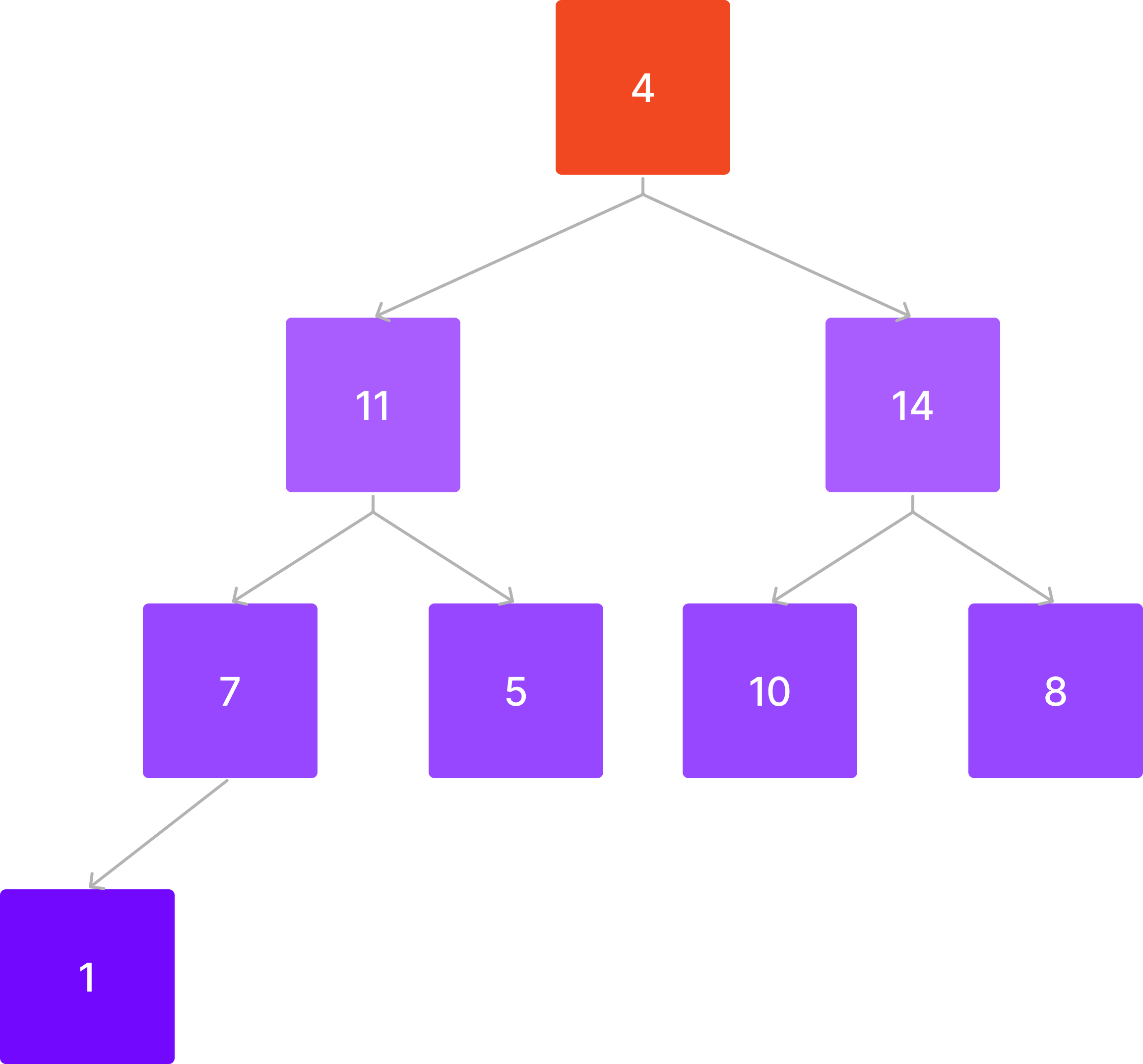
이제 자식 노드 중 큰 노드와 비교해서 교환하는 방식으로 내려간다.

4 < 14이므로 바꾼다.

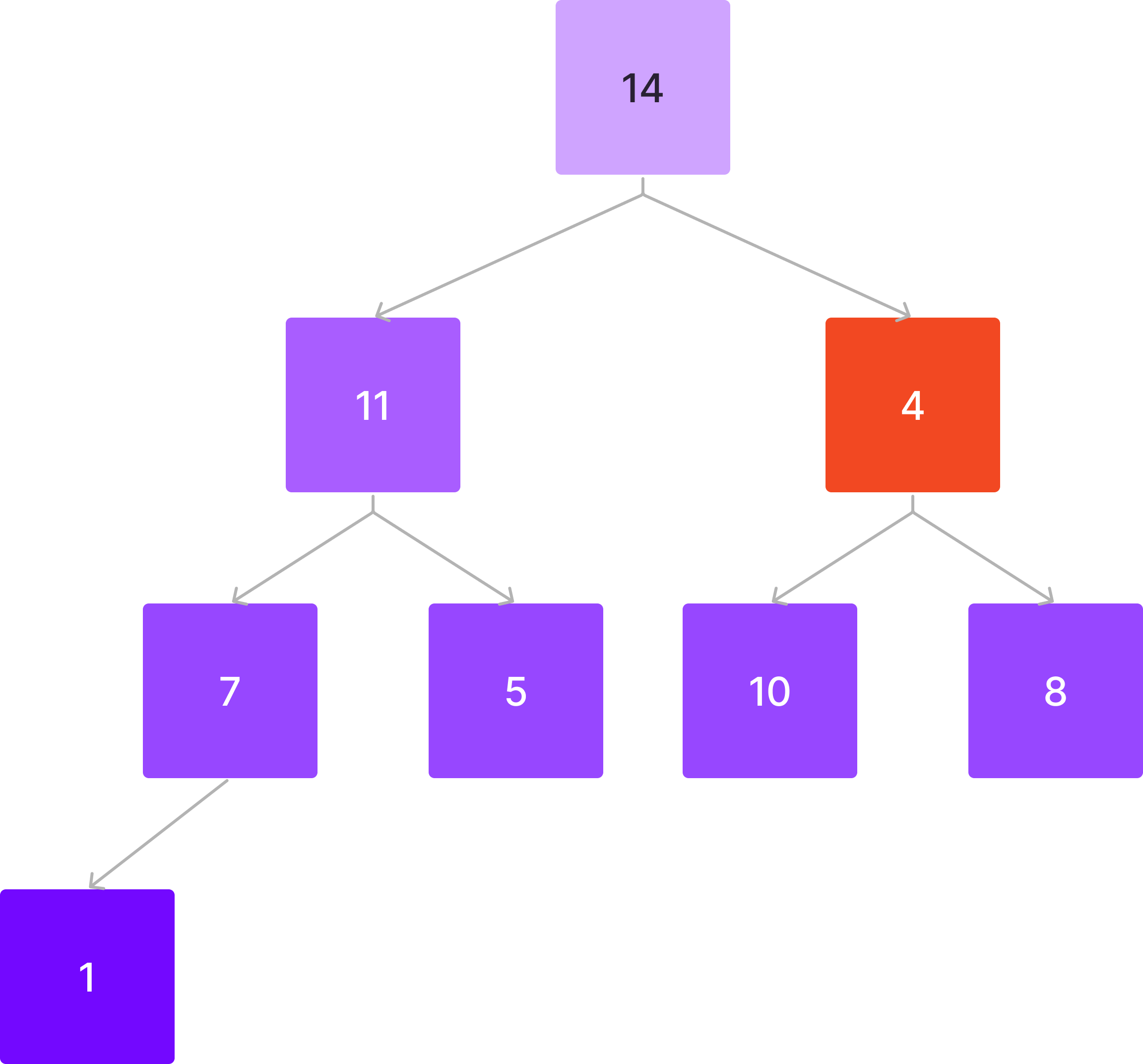
4 < 10이므로 바꾼다.

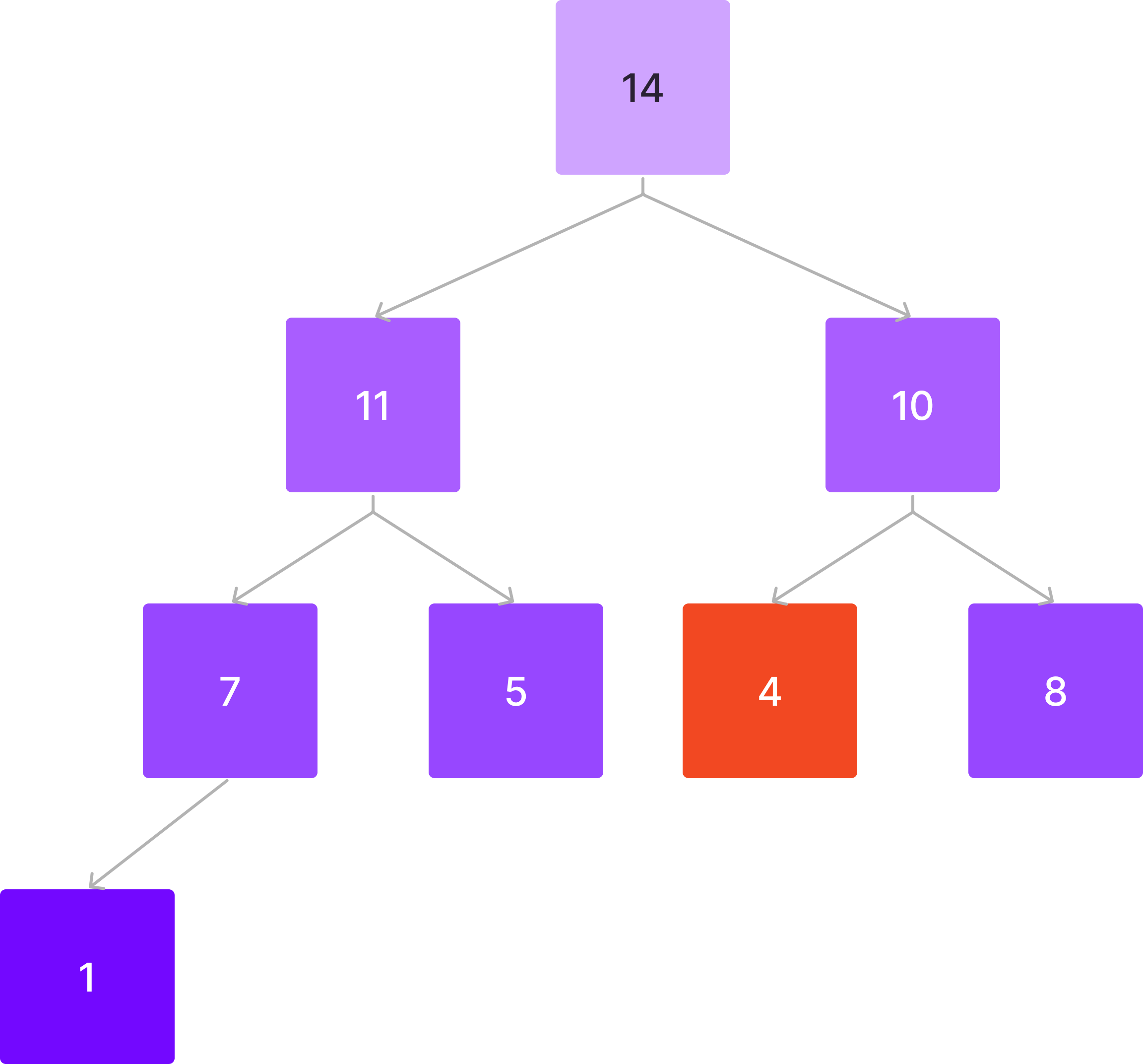
꺼무위키 외 여러개 참고함