문제
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
시작 점
시작 방향
세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.
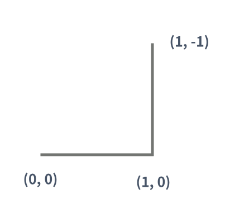
2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)
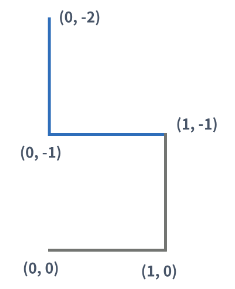
3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.
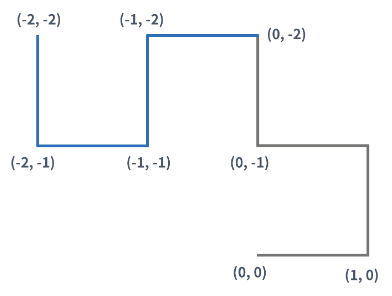
즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입력
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.
방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
0: x좌표가 증가하는 방향 (→)
1: y좌표가 감소하는 방향 (↑)
2: x좌표가 감소하는 방향 (←)
3: y좌표가 증가하는 방향 (↓)
출력
첫째 줄에 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.
풀이
개인적으로 문제를 이해하는 것과 구현 계획을 세우는 것이 까다로웠던 문제라고 생각한다. 나또한 2시간 정도 문제 이해와 구현 계획을 세우다가 도저히 아이디어가 떠오르지 않아 해설을 참고하고 풀었다.
나름 2시간동안 고민해서 그런가..해설을 보아하니 굉장히 쉽게 다가왔다. 이 문제에서 가장 핵심적인 부분은 드래곤 커브의 방향과 순서를 잘 파악하는 것이다.
예시1번을 통해 커브의 방향과 순서를 파악하기에 충분하다.
먼저 예시 1번의 0세대 커브는 쉬우니 넘어가고, 아래의 그림을 보면서 1세대 커브부터 확인해보자 0세대 커브의 끝 점을 기준으로 시계 방향으로 90도 회전한 후, 0세대 커브의 끝점에 붙인 것이다.
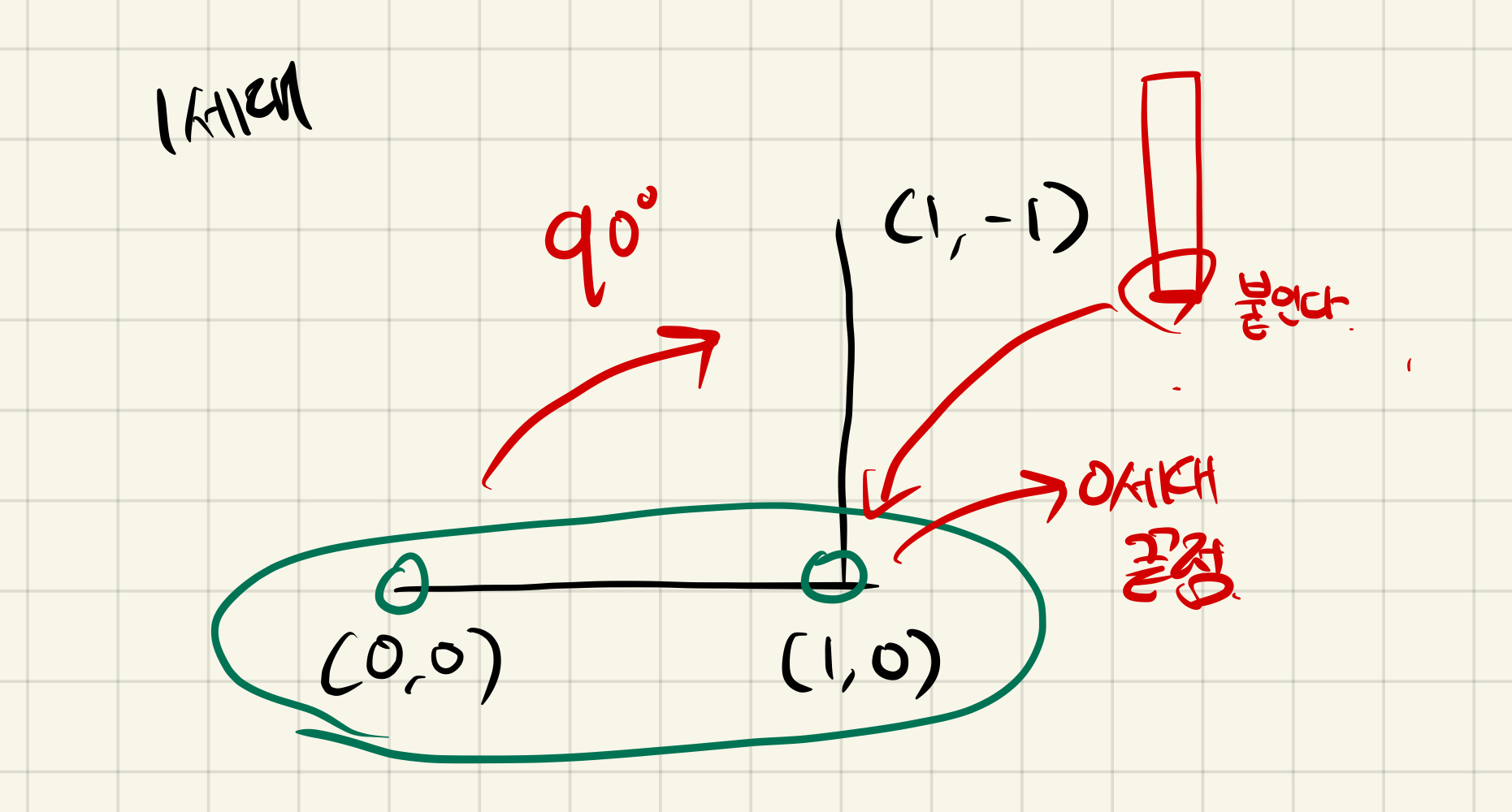
다음으로 2세대 커브로 넘어가보자 그림을 보면 알겠지만 빨간 사선을 기준으로 90도 회전시키면 파란선이 2세대 커브이다. 나머지 3세대 커브도 마찬가지이다. 2세대 끝점인 (0, -2) 기준으로 90도 회전을 시키면 문제에 나와있는 그림이 완성된다.
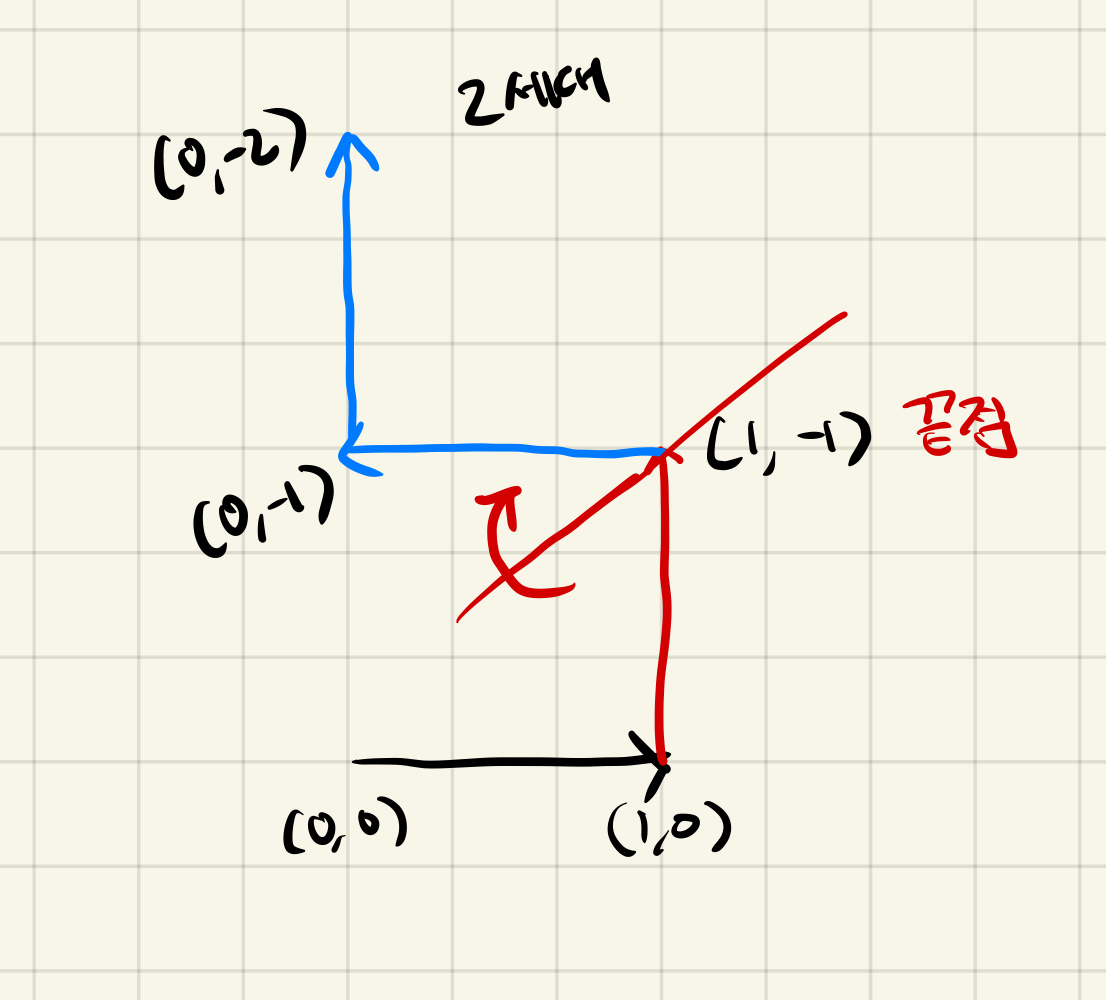
지금까지 우리는 문제에 나와있는대로 직접 손으로 그려보며 어떤 방식으로 결과물이 출력되는지 확인할 수 있었다.
그럼 이제부터 구현을 시작해야한다.
만약 새로운 커브가 생기면 어떤 방식으로 그려줘야할까? 라는 생각을 했을 때 지금까지 그려보았던 그림들을 보면 대략적으로 감을 잡을 수 있다.
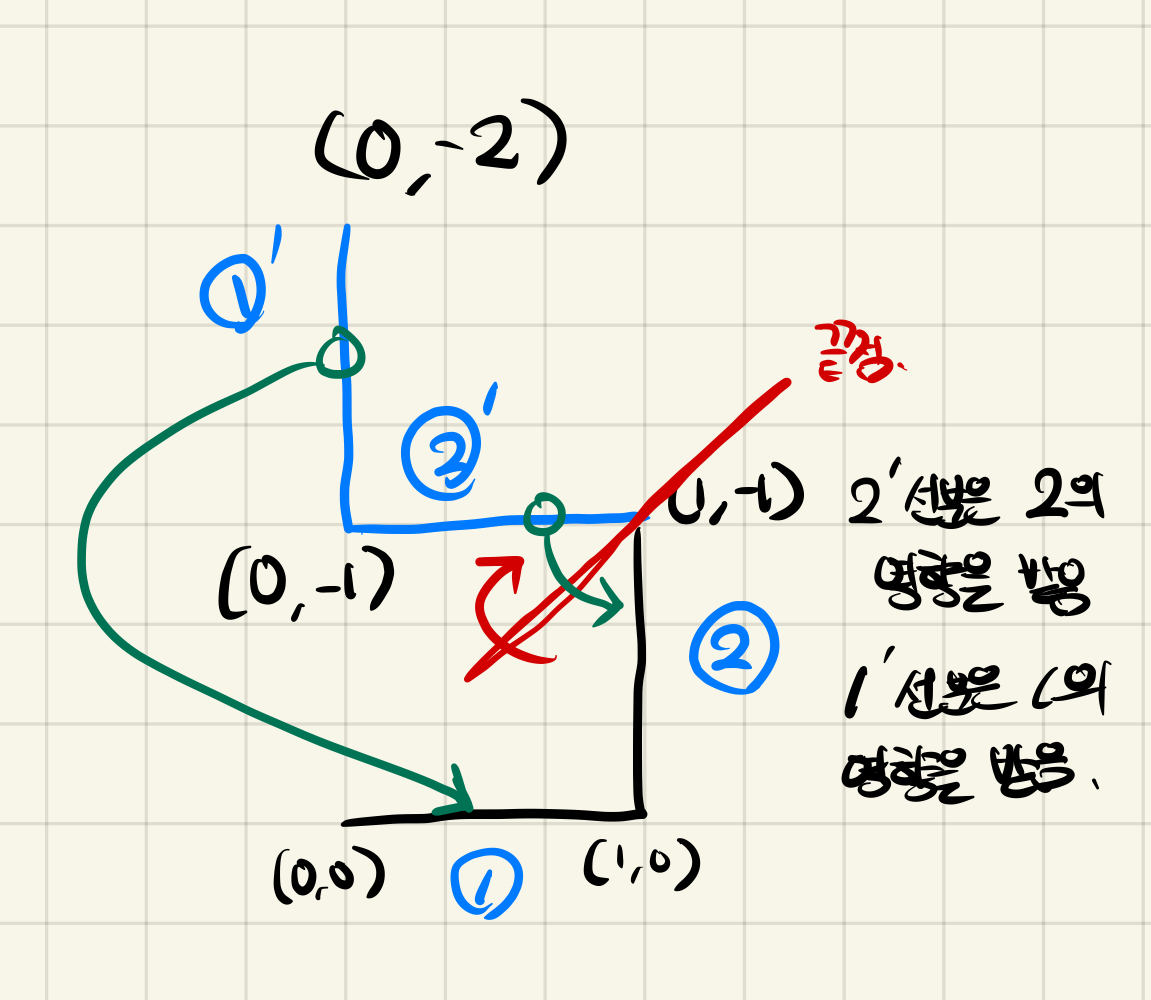
2세대 그림을 기준으로 다시 설명을 해보자면
2' 선분은 2의 영향을 받고, 1' 선분은 1의 영향을 받는 것을 확인할 수 있다.
이를 통해 우리는 하나의 사실을 알아낼 수 있다.
새로운 커브는 기존커브를 반영한다(역순으로) 라는 것을 알 수 있다.
그 다음으로 우리가 구해야 하는 값은 방향 전환 순서이다. 기존에 구한 값은 새로운 커브가 생길때마다 기존커브를 반영한다는 사실만 알았지 실제 커브가 생길때 어느 방향으로 생겨야 하는지는 아직 구하지 않았다.
예시 1번에 마지막 3세대 커브를 보면서 방향 순서를 구해보면 아래의 그림과 같다.
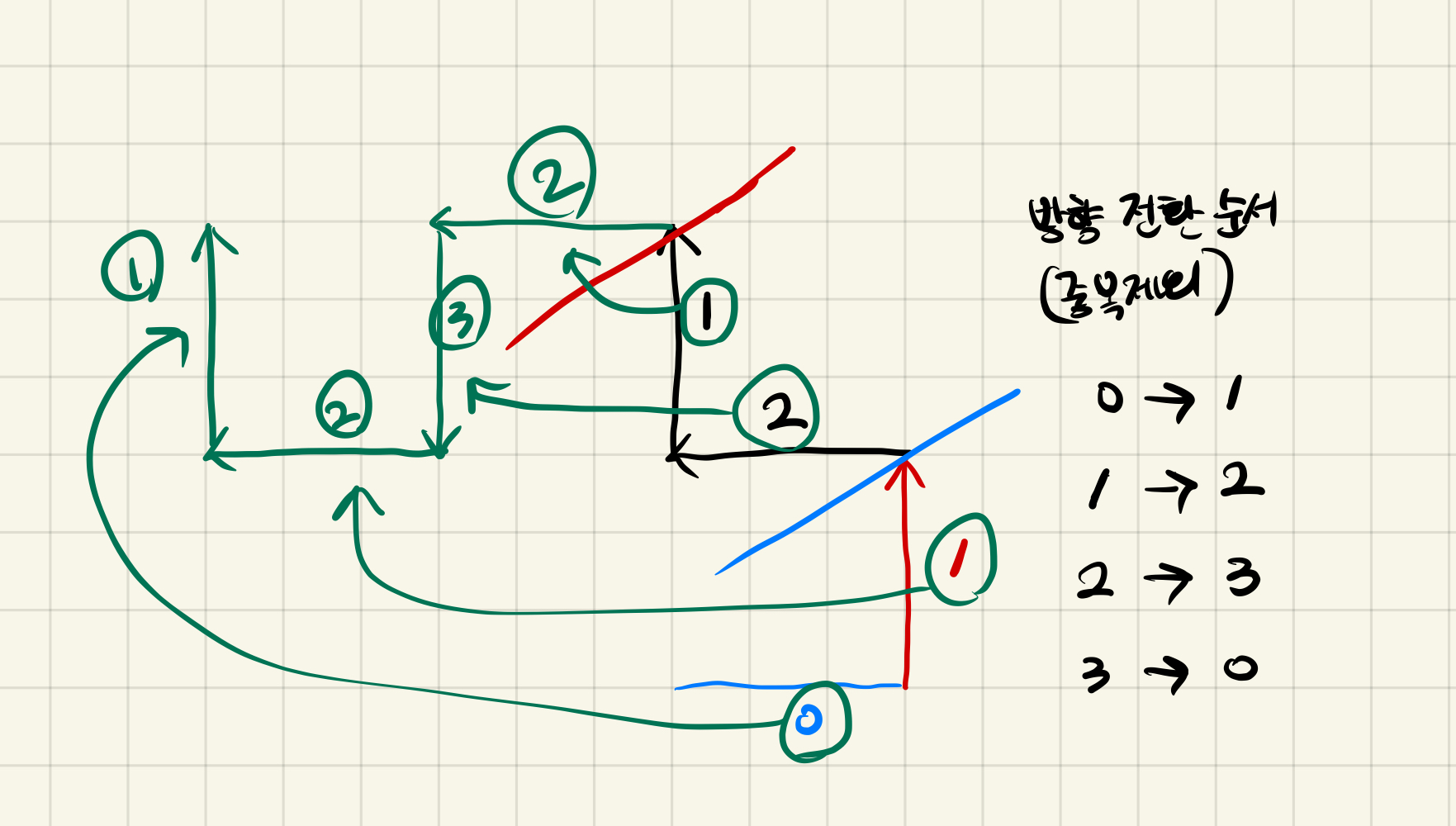
색과 사선을 기준으로 0세대부터 3세대까지 방향 전환이 어떤 방식으로 이루어지는지 그려봤다.
정리하자면 방향이 0일때는 1로가고, 1일때 2, 2일때 3, 3일때 0 으로 회전한다는 것을 알 수 있다.
이제 위 정보를 바탕으로 구현해야하는 것들을 대략적으로 나열해보면 다음과 같다.
- 세대별로 방향을 구하고
- 꼭짓점을 그린다.
- 1 x 1인 정사각형의 수를 구한다.
풀이 소스 코드
import java.io.*;
import java.util.*;
public class _15685_ {
static int N;
static int[] dx = {1, 0, -1, 0};
static int[] dy = {0, -1, 0, 1};
// static int[] dx = {1, 0, -1, 0};
// static int[] dy = {0, 1, 0, -1};
static boolean[][] visited = new boolean[101][101];
static int answer = 0;
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
int g = Integer.parseInt(st.nextToken());
// 드래곤 커브의 정보가 주어질 때마다, 드래곤 커브를 그려야한다.
dragonCurve(x, y, d, g);
}
// 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인지 확인
for (int i = 0; i < 100; i++) {
for (int j = 0; j < 100; j++) {
if(visited[i][j] && visited[i][j+1] && visited[i+1][j] && visited[i+1][j+1]){
answer++;
}
}
}
System.out.println(answer);
}
/**
* 3
* 3 3 0 1
* 4 2 1 3
* 4 2 2 1
*/
private static void dragonCurve(int x, int y, int d, int g) {
// 방향을 담아줄 list 생성
ArrayList<Integer> list = new ArrayList<>();
list.add(d); // 초기 d 입력
for (int i = 1; i <= g; i++) {
for (int j = list.size() - 1; j >= 0 ; j--) {
list.add((list.get(j) + 1) % 4);
}
}
// 구한 방향순으로 선분을 그려야함
visited[y][x] = true;
for (int i = 0; i < list.size(); i++) {
x += dx[list.get(i)];
y += dy[list.get(i)];
visited[y][x] = true;
}
}
}

