프로그래머스 - 기사단원의 무기

문제 출처

문제 출처 : 기사단원의 무기

문제 이해하기

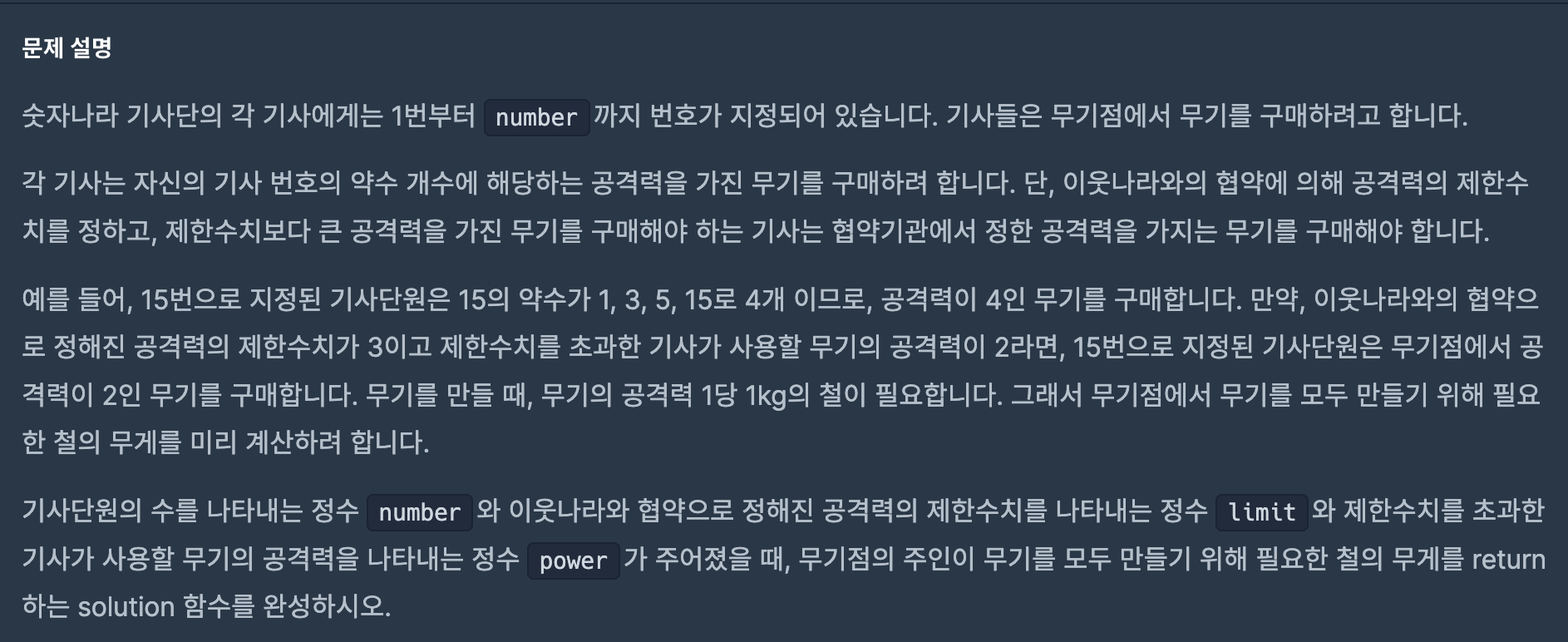
숫자나라 기사단의 각 기사는 1번부터 number까지 번호가 저장되어 있다. 즉 1번 기사 2번 기사...number번 기사까지 있다는 이야기이다.

각 기사는 자기 번호에 해당하는 수의 약수의 갯수와 동일한 공격력을 가진 무기를 가질 수 있다.
하지만 이웃나라와의 협약으로 인해 공격력 제한수치가 걸려있다. 그렇기 때문에 제한수치를 넘는 기사는 이웃나라가 아닌 협약기관에서 정해준 수치의 무기를 구매할 수 있다.

주요 조건 이해하기 ⭐️

이 문제는 지문만 잘 이해하면 금방 풀 수 있는 문제이지만, 문제 제한사항을 자세히보면 number는 최대 100,000 까지 올 수 있다. 다른 의미로는 O(n^2) 방법으로 풀면 시간 초과가 날 확률이 높아진다는 뜻이다.

일반적으로 약수를 구하는 방법은 크게 2가지가 존재한다.

첫번째는 number를 1부터 number까지의 숫자로 나눠 약수인지 판별하는 로직이다.

int number = 10;
int count = 0;
for (int i = 1; i <= number; i++) {
	if (number % i == 0) {
    	count++;
    }
}

이 방법은 1부터 N까지 전부 검증하기 때문에 실행시간이 O(n)이므로, N값이 작을 땐 상관없지만 N값이 커지면 좋지 않은 선택이다.

두번째 방법은 number의 제곱근까지만 반복해주면 되는 로직이다.
이 방법은 실행시간이 O(√n)으로 단축된다.

int number = 10;
int count = 0;
for (int i = 1; i * i <= number; i++) {
	if (i * i == 0) {
    	count++;
    } else if (number  % i == 0) {
    	count += 2;
    }
}

둘 중 하나의 방법을 선택해서 문제를 풀면 된다.

하지만 문제를 잘 이해했다면 1부터 number까지의 대한 약수에 갯수를 각각 구해야 하고 첫번째 방법으로 풀면 실행시간이 O(n^2)이므로 시간초과가 날 것임을 예측할 수 있다.

그렇기 때문에 이 문제는 두번째 방법으로 풀어야만 한다.

제출 코드

class Solution {
    public int getDivisorCount(int number) {
		int count = 0;
		for (int i = 1; i * i <= number; i++) {
			if (i * i == number) {
				count++;
			} else if (number % i == 0) {
				count += 2;
			}
		}
		return count;
	}

	public int solution(int number, int limit, int power) {
		int answer = 0;

		for (int i = 1; i <= number; i++) {

			int count = getDivisorCount(i);

			if (count <= limit) {
				answer += count;
			} else {
				answer += power;
			}
		}

		return answer;
	}
}