문제 출처
문제 출처 : 덧칠하기

문제 이해하기
학교에 페인트가 칠해진 길이가 n미터인 벽이 있다. 중간 중간 이벤트나 행사로 인해 n미터인 벽에 칠해진 페인트가 벗겨지는 일이 발생한다. 학교에서는 예산을 아끼기 위해 벽 전체를 페인트를 칠하는 것이 아닌 1미터 간격으로 n개의 구역을 나누고 왼쪽부터 순서대로 1번부터 n번까지 번호를 붙혔다.
n이 8인 경우 벽의 길이가 8미터 이고 1미터 간격으로 n개의 구역을 나누면 아래와 같이 8개의 구역이 나온다.
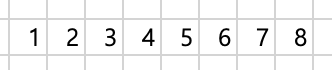
주요 조건 이해하기 ⭐️
벽에 페인트를 칠하는 롤러의 길이는 m미터이고, 이때 칠하는 규칙은 다음과 같다
- 롤러가 벽에서 벗어나면 안된다.
- 구역의 일부분만 포함되도록 칠하면 안된다.
문제를 마지막 문단을 잘 읽어보면 한 구역에 페인트를 여러 번 칠해도 되고 다시 칠해야 할 구역이 아닌 곳에 페인트를 칠해도 상관 없지만 다시 칠하기로 정한 구역은 무조건 한 번은 페인트칠을 해야한다는 것이다.
즉, 아래의 그림처럼 페인트를 다시 칠하는 구역이 2, 3, 6인 경우
2, 3, 6은 반드시 페인트칠을 해야하고 나머지 구역은 몇 번을 페인트칠을 해도 상관없다는 이야기이다.

마지막으로 제한사항을 확인해보면 n,m은 최대 100,000까지 올 수 있다. 만약 이 문제를 O(n^2) 방법으로 푼다면 최대 100억번 연산을 하기 때문에 시간초과가 날 확률이 굉장히 높다.
최초의 생각했던 로직은 단순했다.
- 페인트칠을 한 후 롤러의 위치를 저장할 index 변수를 만든다.
- 입력으로 들어온 section 배열을 순회한다.
- section[i] 번째의 순서에서 롤러의 길이만큼 더 해주고 -1 빼준뒤 롤러의 위치값을 갱신한다.
- -1를 해주는 이유는 i번째부터 시작되기 때문이다.
- 만약 3번 과정에서 구한 롤러의 위치값이 벽의 길이를 초과한 경우, 역으로 롤러의 위치에서 롤러의 길이 m 만큼 빼준다.
이렇게까지 생각했으나, 코드를 작성하다보니 롤러의 인덱스를 선언해놓고 계산하지 않았던 점과 롤러의 위치가 벽을 초과한 경우에 대해 깊게 고민하다보니 최초의 생각했던 로직을 변경하게 되었다.
다시 고민해봤던 로직은
- int형 배열을 벽의 길이만큼 생성해준다.
- 입력으로 들어온 section 배열을 순회하면서 칠해야하는 부분은 1로 만들어준다.
- 다시 벽의 길이 만큼 순회하면서 페인트를 칠하는 영역이 나오면 벽을 벗어난 경우와 벗어나지 않은 경우로 분기처리한다.
- 벽을 벗어난 경우 현재 순회하고 있는 인덱스 i와 롤러의 길이인 m을 빼준 후 이를 역으로 칠한다.
- 벽을 벗어나지 않은 경우는 현재 순회하고 있는 인덱스 i와 롤러의 길이인 m을 더한 후 칠한다.
결국 작성한 코드는 아래와 같다. 문제에 나온 테스트 케이스는 통과했지만 실제 코드를 제출하면 런타임 에러가 발생하거나, 잘못된 값을 반환하는 경우가 많았다.
실패 코드
import java.util.*;
public class PaintBrush {
public int solution(int n, int m, int[] section) {
int answer = 0;
int[] wall = new int[n + 1];
int roller = 0;
for (int i = 0; i < section.length; i++) {
wall[section[i]] = 1;
}
for (int i = 1; i <= n; i++) {
// 덧칠해야하는 경우
if (wall[i] == 1) {
// 벽을 벗어나는 경우
if (i + m > n) {
for (int j = i; j > i - m; j--) {
wall[j] = 0;
}
answer++;
} else {
for (int j = i; j < i + m; j++) {
wall[j] = 0;
}
answer++;
}
}
}
return answer;
}
public static void main(String[] args) {
System.out.println(new PaintBrush().solution(8, 4, new int[]{2, 3, 6}));
System.out.println(new PaintBrush().solution(5, 4, new int[]{1, 3}));
System.out.println(new PaintBrush().solution(4, 1, new int[]{1, 2, 3, 4}));
// System.out.println(202 % 8);
}
}

틀린 이유를 곰곰히 생각해보면, '롤러가 벽을 벗어나면 안된다' 라는 제약조건을 너무 깊게 생각했던 것 같다. 최초의 생각했던 로직을 다시 작성해보면서 코드를 구성했다.
하지만 여기서도 롤러가 벽에서 벗어나는 경우에 대해 계속 생각했었다. 만약 벗어난 경우 어떤 방법으로 쉽게 해결할 수 있을까? 라는 고민을 했다.
고민 끝에 내린 결론은 벗어난 경우는 굳이 지나치게 신경쓸 필요가 없었다. 그 이유는 아래의 예시를 보면
만약 입력으로 n = 7, m = 4, section = {2, 3, 6} 인 경우

한번 칠하게 되면 아래와 같이 된다.

여기서 문제는 6번 구역을 칠할 때 발생하는데 기존의 생각했던 로직은 롤러의 마지막 인덱스에서 롤러의 길이를 더했을 때, 벽의 길이를 초과하게 되면 거꾸로 칠하는 방법을 생각했었다. 이 방법도 좋지만
문제를 다시 이해해보자면, 한 구역에 페인트를 여러 번 칠해도 되고 다시 칠해야 할 구역이 아닌 곳에 페인트를 칠해도 되지만 다시 칠하기로 정한 구역은 적어도 한 번 페인트칠을 해야 합니다. 라는 문장이다.
또한 롤러의 위치와 관련된 조건 자체가 없다. 이 말은 롤러의 시작점이 어디든 상관 없이 다시 칠하기로 정해진 구역은 꼭 페인트칠을 해야한다는 말이기 때문에 거꾸로 칠해야한다는 생각을 하지 않아도 된다.
제출 코드
import java.util.*;
class Solution {
public int solution(int n, int m, int[] section) {
int answer = 0;
int rollerIdx = 0;
for (int i = 0; i < section.length; i++) {
if (section[i] > rollerIdx) {
answer++;
rollerIdx = section[i] + m - 1;
}
}
return answer;
}
}
