1. 정리
- 함수(Function)
: 불려진 시점에 특정한 작업을 수행하며, 입력값과 출력값(반환값, 리턴값)을 가질 수 있다.인자(argument): 함수를 호출할때 전달하는 입력값매개변수(parameter): 함수가 실행될 때 입력값이 들어올 변수반환값(return value): 함수가 종료될 때 호출지점으로 전달할 출력값
- 변수(Variable)
: 값을 가리키는 이름스코프(scope): 변수가 유효한 범위
- 연산자(operator) : 주어진 값들에 대해 정해진 연산을 수행
수리 연산자(mathematical operator): +, -, *, /, \, **비교 연산자(comparison operator): ==, !=, <, >, <=, >=, is논리 연산자(logical operator): and, or
- 제어문(control statements)
: 코드 블럭의 흐름(실행 여부, 반복)을 제어합니다.if: 명제가 참이면 실행합니다.else: if 명제 이외의 경우에 실행합니다.elif: if 명제 이외의 경우에 또 다른 명제가 참일 경우에 실행합니다.while: 명제가 참일 동안 반복합니다.for: 주어진 값들 하나씩 반복합니다.
- 자료형(data types)
: 값들의 종류를 나타냅니다.
정수(int),부동소수점 수(float),불리언(bool),문자열(str),튜플(tuple),리스트(list),딕셔너리(dict)
2. 재귀함수 구현
: 재귀함수란 함수 내에서 그 함수 스스로를 사용하는 함수
피보나치 수열로 재귀함수를 구현해보자.
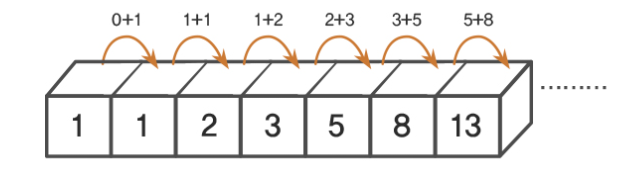
: 피보나치 수열이란 앞의 두 수의 합이 바로 뒤의 수가 되는 수의 배열
def Fibonacci(n):
if n <= 2:
return 1
else:
return Fibonacci(n - 2) + Fibonacci(n - 1)
number = int(input('num : '))
print(Fibonacci(number))
#결과
num : 5
5
num : 7
13위 소스처럼 짜면 입력값이 커질 수록 시간이 매우 오래 걸린다.
이유는 입력값이 3이면, else문으로 빠져 fibonacci() 함수를 2번 더 불러야 합니다. 입력값이 4이면, fibonacci(3)과 fibonacci(2)를 불러야 하고, 여기서 fibonacci(3) 때문에 다시 fibonacci(2)와 fibonacci(1)을 또 부르고... 결국 우리가 짠 코드 상으로는 입력값 n에 대해 fibonacci()함수를 대략 2의 n 제곱 번 불러야 합니다.
한번이라도 계산된 값은 저장을 해놓으면 위 현상이 해결 된다.
memory = {1: 1, 2: 1}
def fibonacci(n):
if n in memory:
number = memory[n]
else:
number = fibonacci(n-1) + fibonacci(n-2)
memory[n] = number
return number
print(fibonacci(10))
print(memory)
#결과
55
{1: 1, 2: 1, 3: 2, 4: 3, 5: 5, 6: 8, 7: 13, 8: 21, 9: 34, 10: 55}프로그래밍에서 이렇게 중간 계산값을 기억해놓고, 다시 계싼하는 대신 값을 바로 읽어 쓰는 방식으로 계싼 시간을 줄이는 기법을 메모이제이션(memoization)이라고 한다.

