
📈 들어가기 앞서
사람들은 불확실성에 대해 자연스러운 반감을 가지고 있는경우가 많다. 특히 전문가들은 '잘 모른다'와 같은 표현을 사용하는 것을 꺼려한다. 사람들은 불확실성을 인정하면서도, 그것이 어떤 단일 수치(점추정)로 제시될때, 추정치에 대한 과도한 믿을을 가진다. 이때 단일 수치가 아닌 어떠한 범위로서 추정치를 제시함으로서 이러한 경향을 막을 수 있다. 이것이 신뢰구간을 표현하는 이유중 하나일 것이다. 먼저, 신뢰구간은 통계적 샘플링에 근거한다.
📈 신뢰구간(Confidence interval)
📈 95% 신뢰구간이란?
100번의 반복 샘플링을 통해 얻은 평균과 편차로 계산한 100개의 신뢰구간중 5개는 실제로 모평균(u,뮤)을 포함하고 있지않는다, 혹은 표본을 통해 얻은 95% 신뢰구간에 실제 모평균이 포함되지 않을 확률이 5%이다.
이때, 95%를 신뢰수준(Confidence Level)이라고 하고 "신뢰수준이 95%이다."라고 말할 수 있다.
신뢰구간이란 모수의 참값이 추정한 구간 안에 포함될 것으로 믿어지는 미리 정해놓은 확신의 정도를 신뢰수준(Confidence Level)이라 한다.
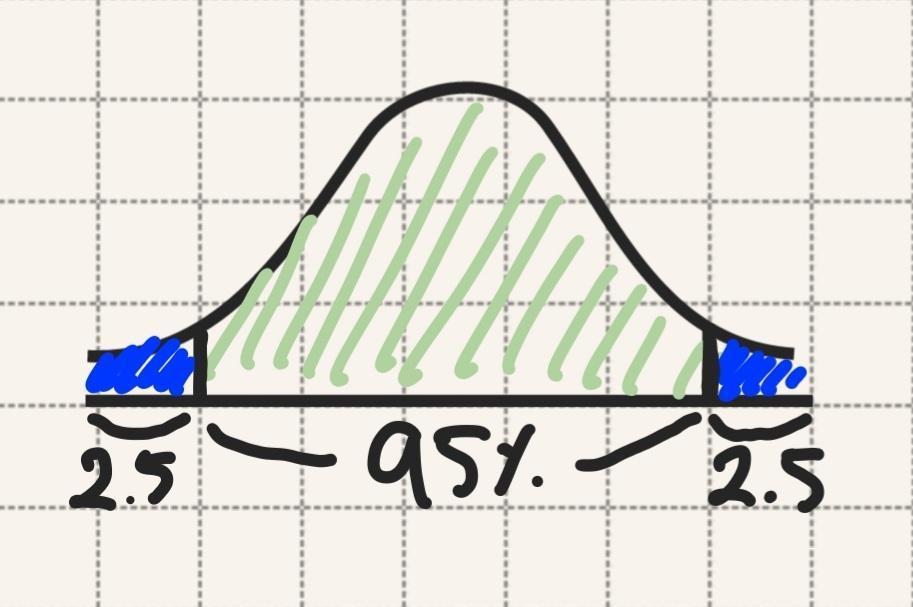
신뢰구간에 대해 그림을 그려보면 위와 같은 모습이다.
이해를 돕기 위해 예시를 하나 들어보고자 한다. 대한민국 남성의 키의 평균을 구해보고자 한다. 하지만 모집단인 대한민국 성인 남성의 키를 모두 측정하는 것은 불가능 하기때문에 여러가지 sampling방법중 하나를 사용하여 sample을 구해서 대표 해보고자 한다.
특별시, 광역시 에서 100명의 성인 남성들을 뽑아 측정한 결과 평균이 170 ~ 180 이라는 결과가 나왔다고 한다. 하지만 sample로 뽑힌 성인 남성 중에서는 195 cm의 키를 보유한 남성도 있을것이다. 반대로 150cm인 남성또한 존재할 수 있다. 이때 신뢰구간을 95%를 잡았다는것은 모든 샘플데이터에서 95%는 포함이 되고 5%는 포함이 되지않는다는 것을 말한다.
150cm, 195cm와 같이 한쪽으로 많이 치우친 값들의 경우 5%에 포함될 확률이 높은것이다. 이는 실제로 sampling을 해봐야 알겠지만 임의로 잡은 평균이 170~180 이라고 가정했을때 150cm과 195cm의 경우를 5%라고 가정해보자.
위의 예시에서 정한 95%의 범위안에 든다면 통계적으로 유의하다고 말할 수 있는 수치이며, 양쪽의 총 5%의 구간은 통계적으로 유의하지 않을 확률이 높다라고 말할 수 있다.
📈 표본의 크기와 신뢰수준의 관계
만약에 표본을 각 특별시, 광역시에서 10명의 사람을 뽑아서 키의 평균이 170 ~172cm가 나왔다고 가정을 해보자. 과연 믿음직 할까?? 별로 믿음직하지 않을것이다. 그런데 만약 50명씩 뽑아서 165에서 175가 나왔다고 해보자. 이것은 좀 더 믿음직하다. 그렇다면 마지막으로 10명씩 뽑아서 키의 평균이 150 ~ 190 이라고 하면 어떨까요?? 이것은 훨씬 믿음직 할 것입니다. 하지만 이것은 정보량이 없습니다. 따라서 우리는 구간을 줄이고 싶을것입니다.
구간을 줄이려면 샘플사이즈를 늘려야지 가능하다. 즉 우리가 165 ~ 175라고 말하고 싶으면 표본의 크기를 100명, 200명, 300명 이렇게 늘려야한다. 즉, 표본크기는 신뢰수준과 밀접한 관계가 있는 것이다.
신뢰수준의 개념을 예시로 한번 더 이해해보자!! 우리가 여론조사를 했다고 가정해 보자.
A후보의 지지율이 40%이고 ±3%라고 하자. 그렇다면 A후보의 실제 지지율이 37% ~ 43%사이에 놓여있을것입니다. 그런데 이것이 항상 성립하는것이 아니라 이러한 여론조사를 백번, 천번, 만번 반복했을때 95번은 참값을 포함할것이고 5번은 틀릴 수 있을것이다 라고 했을때 신뢰수준이 95%이다 라고 할 수 있다. 여기서 5번의 예로는 해당 지지자를 싫어하는 사람들이 sample에 많이 들어갔을 수도 있는 경우를 말한다.따라서 샘플 사이즈를 늘려야 신뢰수준을 늘릴 수 있는것이다.
정리해보면 신뢰수준이 95%라고 동일했을때, 샘플수가 많으면 키의 평균이 165 ~ 175cm라고 이야기 할 수 있지만 샘플수가 10명을 조사한것이라면 150 ~195cm구간으로 늘릴 수 밖에 없는것이다./ 표본이 작을수록 구간이 넓어진다(즉, 불확실성이 더 커진다)
📈 표본크기 N과 관심있는 표본 통계량이 주어졌을때, 부트스트랩 신뢰구간을 구하는 방법
- 데이터에서 복원추출 방식으로 크기 n인 표본을 뽑는다(재표본추출)
- 재표본추출한 표본에 대해 원하는 통계량을 기록한다.
- 1 ~ 2 단계를 R번 반복한다.
- x% 신뢰구간을 구하기 위해, R개의 재표본 결과의 분포 양쪽 끝에서 [(100 - x)/2] % 만큼 잘라낸다.
- 절단한 점들은 x% 부트스트랩 신뢰구간의 양 끝점이다.
부트스트랩은 대부분의 통계량 혹은 모델 파라미터에 대한 신뢰구간을 생성하는 데 사용할 수 있는 일반적인 기법이다.
