기초통계 (20) 재표본추출2(순열검정)

통계학에서 재표본추출이란 랜덤한 변동성을 알아보기위함. 이라는 일반적인 목표를 가지고 관찰된 데이터를 반복추출하는것을 의미하며, 일부 머신러닝(ML)모델의 정확성을 평가하고 향상시키는데 사용할 수 있다.(의사결정트리, 배깅)

📈 재표본추출

• 재표본추출에는 부트스트랩과 순열검정이라는 두 가지 주요 유형이 있다. 기초통계(10)에서 부트스트랩과 간단하게 순열검정도 다루어봤었다. 부트스트랩의 경우 추정의 신뢰성을 평가하기 위해 사용되었으며(신뢰구간), 순열검정에 대해서 이번에 자세히 다루어 보려고 한다.
• 순열검정은 일반적으로 두 개 이상의 그룹과 관련된 가설을 검증하는 데 사용된다.

📈 용어정리

• 순열검정(permutaion test) : 두 개 이상의 표본을 함께 결합하여 관측값들을 무작위로(또는 전부를)재표본으로 추출하는 과정을 말한다.
• 재표본추출 : 관측 데이터로부터 반복해서 표본추출하는 과정

📈 순열검정

• 순열과정에는 두 개 이상의 표본이 관여되며 이들은 보통 A/B 검정 또는 기타 가설검정을 위해 사용되는 그룹들이다.
• 순열검정의 첫 단계는 그룹A와 B의(혹은 C, D... 여러개 가능) 결과를 하나로 합치는 것이다.
• 이렇게 하는 이유는 그룹들에 적용된 처리의 결과가 다르지 않다는 귀무가설의 논리를 구체화 한 것이다.
• 그런다음 결합된 집합에서 무작위로 그룹을 뽑아 가설을 검정하고 얼마나 다른지를 살핀다.
• 순열검정은 비모수적 방법으로 데이터가 정규분포가 아닐때 사용이가능하고 두 변수의 평균의 차이 비교를 예를 들면 30개이상의 sample이거나 정규분포일때 t검정을 그렇지 않을때 순열검정을 쓸 수 있다.

< 순열검정 순서 >

1. 여러그룹의 결과를 단일 데이터 집합으로 결합한다.
2. 결합된 데이터를 잘 섞은 후, 그룹A와 동일한 크기의 표본을 무작위로(비복원) 추출한다.(당연히 다른 그룹의 데이터와 함께 섞었기때문에 포함된다)
3. 나머지 데이터에서 그룹B와 동일한 크기의 샘플을 무작위로(비복원)추출한다.
4. C, D 등 추가적인 다른그룹도 있었다면 해당 그룹에도 똑같은 방법을 사용한다.
5. 원래 샘플(그룹 비율의 차이)에 대해 구한 통계량 또는 추정치가 무엇이었든 간에 새롭게 추출한 재표본에 대해 다시 계산하고 기록한다. 이것으로 순열이 한번 진행된 것이다.
6. 앞의 단계를 R번 반복하여 검정통계량의 순열분포를 얻는다.

• 이제 처음 그룹간의 차이와 비교를 해보면된다.
• 관찰된 차이가 순열로 보이는 차이의 집합안에 들어있으면, 어떠한것도 증명할 수 없다. 즉, 우연히 일어날 수 있는 범위에 있기 때문에 귀무가설이 맞을 확률이 높은것이다.
• 관찰된 차이가 대부분의 순열분포의 바깥에 있다면, 이떄 우연때문이 아니라고 생각해 볼 수 있다. 즉, 이 차이는 통계적으로 유의미 하다는 결론을 낼 수도 있다.

📈 예제

• 사람들의 관심을 오래 끌 수 있는 웹 디자인이 더 많은 매출을 만들 거라고 생각하는 것은 합리적이다. 따라서 측정 지표를 페이지 A와 페이지 B에서의 평균 세션 시간을 비교하는 것으로 정할 수 있다.
• 두가지 서로 다른 디자인에 대해 총 36세션, 페이지A는 21, 페이지 B는 15가 기록이 되었다.BOXPLOT을 통해 비교해 보자

# 데이터 불러오기
session_times = pd.read_csv('/content/web_page_data.csv')
session_times

• 위 사진은 데이터의 일부이다.

# visualization
ax = session_times.boxplot(by = 'Page', column = 'Time')
ax.set_xlabel('')
ax.set_ylabel('Time (in seconds)')
plt.suptitle('') # 모든 서브플롯에 메인타이틀을 부여한다.

위의 boxplot을 보면 페이지 B가 방문객들을 더 오래 붙잡은 것으로 나타난다.

• 각 그룹의 평균을 확인해보면

mean_a = session_times[session_times.Page =='Page A'].Time.mean()
mean_b = session_times[session_times.Page =='Page B'].Time.mean()

print(f'mean_a : {mean_a}')
print(f'mean_b : {mean_b}')
print(f'mean_b - mean_a: {mean_b - mean_a}')
>>>
mean_a : 126.33333333333333
mean_b : 162.0
mean_b - mean_a: 35.66666666666667

• 페이지 B는 페이지 A와 비교하여 세션시간이 평균 35.67초 정도 더 길다.
• 하지만, 우리가 확인하고 싶은것은 지금나온 이 차이가 우연에 의한 것인지를 판단하는것이다.
• 순열검정을 통해 모든 세션 시간을 결합한 다음, 잘 섞은 후 21개의 그룹(A페이지의 경우 21)과 15개의그룹(B의경우 15)으로 반복하여 표본을 추출한다.
• 순열검정을 적용하기위해서는 36개의 세션 시간을 21개 와 15개의 그룹에 랜덤하게 할달해야한다.

# 순열검정을 구현하는 함수
import random

def perm_fun(x, nA, nB):
  n = nA + nB # 두개의 데이터를 단일로 합쳐준다.
  idx_B = set(random.sample(range(n),nB)) # 1. 비복원 추출 방식으로 nB개의 표본을 추출하여 그룹 B에 할당
  idx_A = set(range(n)) - idx_B # 2. 나머지 nA개는 그룹 A에 할당
  return x.loc[idx_B].mean() - x.loc[idx_A].mean() # 두 그룹 간 평균 차이 계산

# 페이지 A, B의 갯수 저장
nA = session_times[session_times.Page == 'Page A'].shape[0] 
nB = session_times[session_times.Page == 'Page B'].shape[0]

• perm_fun 함수는 비복원추출 방식으로 nB개의 표본을 추출하고 그룹 B에 할당한다.
• 나머지 nA개를 그룹 A에 할당한다.
• 이때 두 평균의 차이를 결과로 반환한다.

# 함수를 1000번 호출하여 히스토그램 시각화

random.seed(1)
perm_diffs = [perm_fun(session_times.Time, nA, nB) for _ in range(1000)]

fig, ax = plt.subplots(figsize=(5, 5))
ax.hist(perm_diffs, bins=11, rwidth=0.9)
ax.axvline(x = mean_b - mean_a, color='black', lw=2)
ax.text(50, 190, 'Observed\ndifference', bbox={'facecolor':'white'})
ax.set_xlabel('Session time differences (in seconds)')
ax.set_ylabel('Frequency')

plt.tight_layout()
plt.show()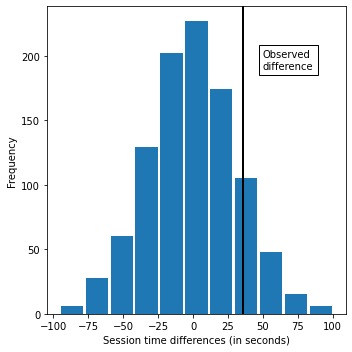

import numpy as np
print(np.mean(perm_diffs > mean_b - mean_a))
>>> 0.121 

• 페이지 A와 페이지 B사이의 세션 시간의 차이가 확률분포의 범위 내에 있음을 의미하며, 12.1%의 확률로 차이가 있을 수도 있다. 따라서 차이는 통계적으로 유의하지 않다.

📈 순열검정 : 데이터 과학의 최종 결론

• 순열검정은 랜덤한 변이가 어떤 역할을 하는지 알아보기 위해 사용되는 휴리스틱한 절차이다.
• 이는 상대적으로 코딩하고, 해석하고, 설명하기 쉽다. 그리고 정확성을 보증할 수 없는, 수식에 기반을 둔 통계학이 빠지기 쉬운 형식주의와 '거짓 결정론'에 대한 유용한 우회로를 제공한다.

📈 주요개념

• 순열검정에서는 여러 표본을 결합한 다음 잘 섞는다.
• 그런 다음 섞인 값들을 이용해 재표본추출 과정을 거쳐, 관심 있는 표본통계량을 계산한다.
• 이과정을 반복하여 재표본추출한 통계를 도표화한다.
• 관측된 통계량을 재표본추출한 분포와 비교하면 샘플간에 관찰된 차이가 우연에 의한 것인지를 판단할 수 있다.