기초통계 (24) 분산분석(아노바검정)

📈 용어정리

• 쌍별 비교 : 여러 그룹 중 두 그룹 간의 가설검정
• 총괄검정 : 여러 그룹 평균들의 전체 분산에 관한 단일 가설검정
• 분산분해 : 구성요소 분리. 예를 들면 전체 평균, 처리평균, 잔차 오차로부터 개별 값들에 대한 기여를 뜻한다.
• F 통계량 : 그룹 평균 간의 차이가 랜덤모델에서 예상되는 것에서 벗어나는 정도를 측정하는 표준화된 통계량
• SS(sum of squares) : 어떤 평균으로부터의 편차들의 제곱합

📈 분산분석

• 여러 그룹간의 통계적으로 유의미한 차이를 검정하는 통계적 절차를 분산분석이라고 하며, 줄여서 ANOVA(아노바)라고 한다.

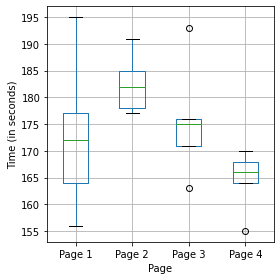
• 4개 웹페이지의 점착성, 즉 방문자가 페이지에서 보낸 시간을 의미하며 초 단위로 보여준다.

• 각 페이지는 총 5명의 방문자가 있으며 독립적인 데이터 집합이다.

• 단지 두 그룹을 비교하는 것이라면 문제는 단순할 것이지만 5개의 평균에 대해서 그룹간의 6가지 비교를 해야한다.

1페이지와 2페이지 비교
1페이지와 3페이지 비교
1페이지와 4페이지 비교
2페이지와 3페이지 비교
2페이지와 4페이지 비교
3페이지와 4페이지 비교

• 한 쌍씩 비교하는 횟수가 증가할 수록 우연히 일어난 일에 속을 가능성이 커진다. 따라서 전체적인 총괄검정을 할 수 있는 ANOVA가 여기서 사용된다.

• ANOVA를 토대로 재표본추출 과정을 살펴보자

1. 모든 데이터를 한 상자에 모은다.
2. 5개의 값을 갖는 4개의 재표본을 섞어서 추출한다.
3. 각 그룹의 평균을 기록한다.
4. 네 그룹 평균 사이의 분산을 기록한다.
5. 2 ~ 4단계를 여러 번 반복한다.(예를 들면 1,000번)

• 재표본추출한 분산이 관찰된 변화를 초과한 시간은 어느 정도일까? 이것이 바로 p값이다.

observed_variance = four_sessions.groupby('Page').mean().var()[0]
print('Observed means:', four_sessions.groupby('Page').mean().values.ravel())
print('Variance:', observed_variance)
# Permutation test example with stickiness
def perm_test(df):
    df = df.copy()
    df['Time'] = np.random.permutation(df['Time'].values)
    return df.groupby('Page').mean().var()[0]
    
print(perm_test(four_sessions))

>>>
Observed means: [172.8 182.6 175.6 164.6]
Variance: 55.426666666666655
21.61333333333339

📈 F통계량

• 두 그룹의 평균을 비교하기 위해 순열검정 대신 t검정을 사용할 수 있는것처럼, F통계량을 기반으로 ANOVA통계 검정도 있다.
• F통계량은 잔차 오차 로 인한 분산과 그룹평균(처리효과)의 분산에 대한 비율을 기초로 한다. 이비율이 높을수록 통계적으로 유의미 하다고(차이가 있다)볼 수 있다.
• F값 = 그룹간 분산 / 그룹내 분산 => 이 비율이 높을 수록 그룹간의 차이가 우연히 발생하지 않은것이므로 통계적으로 유의미 하다.
• statsmodels 패키지는 파이썬에서 ANOVA구현을 제공한다.

from scipy import stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats import power

model = smf.ols('Time ~ Page', data=four_sessions).fit()
                
aov_table = sm.stats.anova_lm(model)
print(aov_table)

>>>

            df  sum_sq     mean_sq         F    PR(>F)
Page       3.0   831.4  277.133333  2.739825  0.077586
Residual  16.0  1618.4  101.150000       NaN       NaN

Df는 자유도, Sum Sq는 제곱합, Mean Sq는 평균제곱(평균제곱편차), F value는 F통계량 을 가리킨다.

res = stats.f_oneway(four_sessions[four_sessions.Page == 'Page 1'].Time, 
                     four_sessions[four_sessions.Page == 'Page 2'].Time,
                     four_sessions[four_sessions.Page == 'Page 3'].Time,
                     four_sessions[four_sessions.Page == 'Page 4'].Time)
print(f'F-Statistic: {res.statistic / 2:.4f}')
print(f'p-value: {res.pvalue / 2:.4f}')

>>>
F-Statistic: 1.3699
p-value: 0.0388

📈 이원분산분석

• 지금까지 설명한 분산분석은 변하는 요소(그룹)가 하나인 '일원'ANOVA이다. 하지만, 주말대 평일 이라는 두번째 요소를 고려하면(그룹A주말, 그룹A평일,그룹B주말, 그룹B평일..)에 관한데이터가 있다고 가정하자. 이때 필요한 것이 이원ANOVA이다.

• 이러한 여러요인과 효과를 모델링 할 수 있는 회귀와 로지스틱 회귀같은 완전한 통계 모델을 위한 첫걸음이 바로 이원 ANOVA이다.