기초통계 (28) 단순선형회귀

📈 용어정리

• 응답변수(반응변수, 종속변수) : 예측하고자 하는 변수
• 독립변수(예측변수, 독립변수) : 응답치를 예측하기 위해 사용되는 변수
• 레코드(record) : 한 특정 경우에 대한 입력과 출력을 담고 있는 벡터(행, 사건)
• 절편 : 회귀직선의 절편, X = 0일때 예측값
• 회귀계수(regression coefficient) : 회귀직선의 기울기
• 적합값(fitted value),예측값 : 회귀선으로부터 얻은 추정치($\hat{Y_i}$)
• 잔차(residual) : 관측값과 적합값의 차이
• 최소제곱(least square) : 잔차의 제곱합을 최소화하여 회귀를 피팅하는 방법

📈 단순선형회귀

• 한 변수와 또 다른 변수의 크기 사이에 어떠한 관계이다.

• 예를 들면 X가 증가할때 Y의 움직임(증가, 감소)의 관계에 대한 모델을 제공한다.

• 상관관계와 회귀를 비교해 보면 상관관계는 두 변수 사이의 전체적인 관련 강도를 측정하는 것이라면, 회귀는 관계 자체를 정량화하는 방법이다.

• 회귀식 : $Y = b_0+b_1x$

• $b_0$은 절편(상수) 그리고 $b_1$은 $X$의 기울기라고 하며 보통 $b_1$을 주로 계수(coefficient)라고 한다.

• 변수 Y 는 X에 따라 달라지기 때문에 응답변수 혹은 종속변수 라고 부른다. 반면, 변수 $x$는 독립변수 혹은 예측변수라고 부른다.

예시) 노동자들이 면진에 노출(Exposure)된 연수와 폐활량(PEFR)을 표시한 것이다. 어떤 관계가 있을까??

lung = pd.read_csv('/content/LungDisease.csv')

lung.plot.scatter(x='Exposure', y='PEFR')

plt.tight_layout()
plt.show()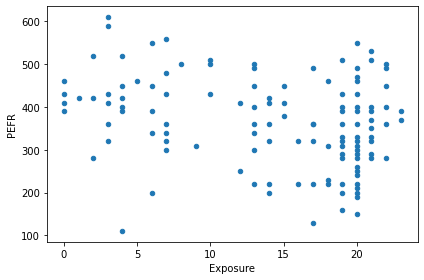

• 위의 그림만 봐서는 어떠한 관계가 있는지 확인하기 어렵다
• 단순성형회귀는 예측변수 Exposure에 대한 함수로 응답변수 PEFR을 예측하기 위한 가장 최선의 직선을 찾으려고 시도할 것이다.
  $PEFR = b_0 + b_1노출$

from sklearn.linear_model import LinearRegression

predictors = ['Exposure']
outcome = 'PEFR'

model = LinearRegression()
model.fit(lung[predictors], lung[outcome])

print(f'Intercept: {model.intercept_:.3f}')
print(f'Coefficient Exposure: {model.coef_[0]:.3f}')

>>>

Intercept: 424.583
Coefficient Exposure: -4.185

$b_0$(절편) = 424.583 : 노동자가 노출된 연수가 0일때 예측되는 PEFR이라고 해석이 가능하다.

$b_1$(회귀계수) = -4.185 : 노동자가 면진에 노출되는 연수가 1씩 증가할때마다, PEFR은 -4.185의 비율로 줄어든다고 해석이 가능하다.

좀 더 보기쉽게 확인해 보자

import numpy as np

fig, ax = plt.subplots(figsize=(4, 4))
ax.set_xlim(0, 23)
ax.set_ylim(295, 450)
ax.set_xlabel('Exposure')
ax.set_ylabel('PEFR')
ax.plot((0, 23), model.predict([[0], [23]]))
ax.text(0.4, model.intercept_, r'$b_0$', size='larger')

x = [[7.5], [17.5]]
y = model.predict(x)
ax.plot((7.5, 7.5, 17.5), (y[0], y[1], y[1]), '--')
ax.text(5, np.mean(y), r'$\Delta Y$', size='larger')
ax.text(12, y[1] - 10, r'$\Delta X$', size='larger')
ax.text(12, 390, r'$b_1 = \frac{\Delta Y}{\Delta X}$', size='larger')

plt.tight_layout()
plt.show()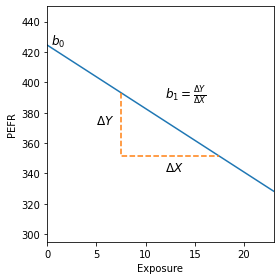

방금 만든 모델의 회귀선은 위와 같다.

📈 적합값과 잔차

• 회귀분석에 중요한 개념은 예측값(적합값)과 잔차(예측 오차)이다. 보통 모든 데이터가 정확하게 한 직선안에 들어오지는 않는다. 따라서 회귀식은 명시적으로 오차항 $e_i$를 포함한다.

$Y_i = b_0 + b_1X_i + e_i$

• 예측값은 보통 $\hat{Y_i}$(Y햇)으로 나타낸다. 다음과 같이 수식으로 쓸 수 있다.

• $\hat{Y_i}$ = $\hat{b_0}$ + $\hat{b_1}X_i$

• $\hat{b_0}$ 과 $\hat{b_1}$ 은 이미 알려진 값이 아닌 추정을 통해 얻은 값이라는 것을 의미한다.

• 여기서 잔차 $\hat{e_i}$는 원래 값에서 예측한 값을 빼서 구한다.

• $\hat{e_i}$ = $Y_i$ - $\hat{Y_i}$

• 사이킷런의 LinearRegression모델을 사용하여 훈련 데이터에 대한 predict메서드를 사용하여 fitted(예측값)값 과 그에 따른 residuals(잔차) 를 얻을 수 있다.

# 예측값과 잔차
fitted = model.predict(lung[predictors])
residuals = lung[outcome] - fitted

# 시각화
ax = lung.plot.scatter(x='Exposure', y='PEFR', figsize=(4, 4))
ax.plot(lung.Exposure, fitted)
for x, yactual, yfitted in zip(lung.Exposure, lung.PEFR, fitted): 
    ax.plot((x, x), (yactual, yfitted), '--', color='C1')

plt.tight_layout()
plt.show()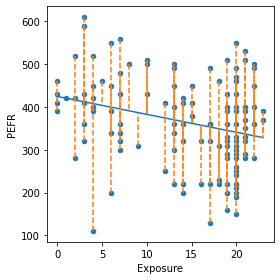

• 폐활량에 대한 회귀선으로부터 얻은 잔차를 설명한다. 데이터 포인트에서 직선 사이에 수직으로 그은 점선을 바로 잔차(residual)를 의미한다.

📈 최소제곱

• 그렇다면 이런 데이터를 어떻게 피팅한 모델로 만들수 있을까???

• 가장 흔하게 쓰이는 것은 잔차들을 제곱한 값들의 합인 잔차제곱합(residual sum of squares, RSS)을 최소화하는 선이다.
  

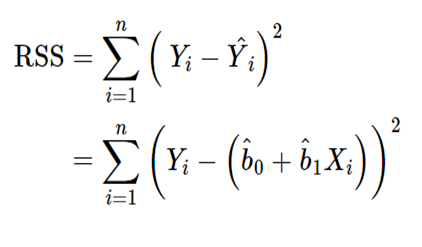
• 추정치 $\hat{b_0}$ 과 $\hat{b_1}$ 은 RSS를 최소화 하는 값이다.

• 즉, 잔차제곱합이 최소가 되려면 $\hat{b_0}$ 과 $\hat{b_1}$ 이 최소가 되어야 한다는 뜻이다.

• 이렇게 잔차제곱합을 최소화 하는 방법을 최소제곱회귀 또는 보통최소제곱(ordinary least square, OLS)회귀 라고 한다.

• 하지만, 최소제곱은 평균과 마찬가지로 특잇값(Outlier)에 매우 민감하다.