독립표본T 검정, 대응표본 검정

유의성 검정에 대하여

모든 유의성검정은 관심 있는 효과를 측정하기 위해 검정통계량을 지정한다, 그리고 관찰된 효과가 정상적인 랜덤변이의 범위 내에 있는지 여부를 판단하는 데 도움을 준다.

T-test

T검정이란 가설검정의 한 종류로서 모집단의 분산이나 표준편차를 알지 못할때, 표본으로부터 추정된 분산이나 표준편차를 이용하여, 두 모집단의 평균의 차이를 통해 집단이 같은지, 다른지 알아보는 검정 방법이다.

예를들어 성별에 따른 시험성적점수의 차이를 구할때 즉 성별이라는 독립변수(범주형,질적변수),에 따른 시험점수(연속형,양적변수)의 차이 이런것을 보고싶을 때 분석하는것이 독립표본 T검정이다.

집단의 수가 3개 이상인 경우 ANOVA(아노바)검정을 사용한다.

T검정의 귀무가설과 대립가설

• T검정에서 귀무가설은 1sample의 경우 특정값과 평균의 차이가 같다. 2sample의 경우 2개의 sample의 평균의 차이는 같다

• T검정에서 대립가설은 1sample의 경우 특정값과 평균의 차이가 같지않다. 2sample의 경우 2개의 sample의 평균의 차이는 같지않다.

T검정은 언제 사용해야 할까??

• 종속변수가 양적 변수(Numerical)일때
• 모집단의 표준편차를 알지 못할 때
• 모집단의 분포가 정규분포를 따를때
• 평균의 차이로 집단(샘플들)이 유사한지 알아볼 때

(즉, T검정은 표본의 평균이 특정값 혹은 또다른 표본의 평균과의 차이를 알아보는것으로서 100명이 A홈페이지의 접속을 했을 때 접속시간이 100개의 데이터로 있는데 이것이 0.01초와 차이가있는가(단일표본t검정, 신뢰구간을 통해확인) 또는 B홈페이지의 100명의 접속시간 데이터와 비교해서 만약 A가 0.01초 빨랐는데 이것이 우연에 의한 차이인지 아닌지를 신뢰구간과 연결지어 T검정을 통해 확인한다)

T검정의 종류

1) 단일표본 T검정(One-Sample-test)

1개의 sample값들의 평균이 특정값과다르다고 할 수 있는지 검증(stats.ttest_1samp(sample,특정값)

import numpy as np
np.random.seed(42)
np.random.binomial(n = 1, p = 0.5, size =1000)
# 우연히 동전의 앞면 혹은 뒷면(1로지정)이 나올확률이 0,5인것을 1000번 하겠다.
coin = np.random.binomial(n = 1, p = 0.5, size = 1000)

from scipy import stats
stats.ttest_1samp(coinflips, .5)

>>> Ttest_1sampResult(statistic = -1.2019326366894174, pvalue = 0.229674463143974)

p-value > 0.05(기준) 귀무가설은 기각되지 않는다.

2) 독립표본 T검정(Two-Sample-test)

2개의 sample값들의 평균이 서로 다르다고 할 수 없는지 비교하는것(stats.ttest_ind(sample1, sample2, equal_var = True or False)

np.random.seed(111)
coinA = np.random.binomial(n =1, p = 0.6, size = 500)
coinB = np.random.binomial(n =1, p = 0.5, size = 200)
satats.ttest_ind(coinA, coinB)

>>> Ttest_indResult(statistic = 2.5217925052968604, pvalue = 0.011897284906103032)

p-value < 0.05(기준) 귀무가설은 기각된다.
즉, coinA와 coinB는 서로 동일하다고 보기 어렵다.

양측검정과 단측검정

1) 독립표본 단측검정(Two-Sample-one-tailed-test)

두 개의 sample이 있을때 A는 B보다 크다 혹은 작다라는 내용이 있으면 단측검정을 뜻한다.
이때는 stats.ttest_ind에서 alternative='greater' 혹은 alternative = 'less'를 통해 어떤 변수가 큰지 지정해 주면된다.

stats.ttest_ind(A,B,alternative = 'greater') # A가 B보다 크다
stats.ttest_ind(A,B,alternative = 'less') # A가 B보다 작다 or B가 A보다 크다

2) 독립표본 양측검정(Two-Sample-two-tailed-test)

두 개의 sample A, B가 있을때 A와 B는 같다, A 와 B는 같지않다 이렇게 두가지로 나누어 질때 사용한다.

np.random.seed(42)

coinA = np.random.binomial(n= 1, p = 0.5, size =500)
coinB = np.random.binomial(n= 1, p = 0.5, size =200)

stats.ttest_ind(coinA, coinB)

T검정의 조건

• 독립성
  - 독립변수의 그룹군은 서로 독립적
• 정규성
  - 독립변수에 따른 종속변수는 정규분포를 만족
• 등분산성
  - 모든 그룹에 데이터에 대한 분산이 같아야 한다.

1) 독립성
(독립표본 T검정의 경우,2sample t-test)두 집단은 서로 독립적이어야 한다. 독립적이라는 것은 두개의 집단을 구성하는 구성원이나 구성들이 서로 관계가 없다는 것을 의미한다. 즉, 아무런 관계가 없는것은 집단 간 독립적이다 라고 표현할 수 있다.

하지만, 두 집단을 대표한다고 볼 수 있는 평균을 비교할때 항상 독립적이기만 할 수 없다는 것입니다. 예를들어 동일한 대상 K를 새로 개발한 약물의 효과가 있는지를 알아보기 위해서는 K에게 약물을 복용하기 전과 후를 비교해야한다. 즉, 동일한 K라는 대상에게 사전(pre)과 사후(post)를 비교할때 주로 사용하는것이 있는데 이것을 대응표본(paired sample)이라고 부른다.(대응표본에 대해서는 밑에서 설명하겠다.)

2) 정규성
정규성이란 수집된 데이터가 특정한 값에 편중되지않고 적절하게 수집이 되었는지를 확인하는 과정입니다.
정규성을 확인하기 위한 자료 분포를 정규 분포 라고 한다.

일반적으로 각 집단에서 30개 이상의 측정값을 확보한 경우에는 자료가 정규성을 가진다 라는 말이 있다. 여기서 주의 할 점은 집단에서 확보한 30개의 측정값 자체의 정규성을 의미하는 것이 아니라 30개의 측정값의 평균이 가지는 정규성을 말한다.

즉, 독립표본T검정(2sample t-test)에서 두 집단의 수치를 하나 하나 비교하는것이 아니라 각각의 집단의 평균을 비교하는 것이다. 따라서 정규성을 가지는 것은 평균이 가지는 정규성을 의미한다.

위에서 말한 표본수가 30개 이상일때 표본평균은(sample mean) 모집단의 자료분포와 상관없이 정규분포를 따른다는 것은 중심극한정리(CLT)를 통해 증명된 사실이다.

만약 30개 미만이면 정규성 검정을 해야하는데 만족하면 독립표본T검정을 사용하고 만족하지 못하면 윌콕슨의 순위합 검정을 사용할 수 있다.

30개 미만일때 정규성 검증 방법으로는 Kolmogorov-Smirnov test와 Shapiro-Wilk test방법이 있다.

• Kolmogorov-Smirnov test(KS-test),1sample

from scipy.stats import kstest #1samp kstest
import numpy as np

np.random.seed(42)
x = np.random.normal(0, 1, 1000)
kstest(x,'norm')

>>> KstestResult(statistic=0.017327787320720822, pvalue=0.9196626608357358)

• Kolmogorov-Smirnov test(KS-test),2sample

from scipy.stats import ks_2samp #2samp kstest
import numpy as np

np.random.seed(42)
x = np.random.normal(0, 1, 1000)
y = np.random.normal(0, 1, 1000)
z = np.random.normal(-1.2,1.1, 1000)

print("x와 y:",ks_2samp(x, y))
print("x와 z:",ks_2samp(x, z))

>>>
x와 y: KstestResult(statistic=0.045, pvalue=0.26347172719864703)
x와 z: KstestResult(statistic=0.447, pvalue=2.6573756410355674e-90) 

3) 등분산성
두 군의 분산이 동일한지 안한지를 확인하는것

# 정규성과 같은데이터(x,y,z)
from scipy import stats
stats.levene(x, y)

>>>LeveneResult(statistic=0.16575791865118406, pvalue=0.6839533428776543)
# x와 y는 등분산이다(0.05기준)

from scipy import stats
stats.levene(y, z)

>>>LeveneResult(statistic=6.783703349101153, pvalue=0.00926758742043179)
# x와 y는 등분산이 아니다(0.05기준)


#등분산성의 귀무가설 : 등분산이다
#등분산성의 대립가설 : 등분산이 아니다.
stats.levene(sample1, sample2)

# 등분산을 만족한다면.
stats.ttest_ind(A,B, equal_var = True)
# 등분산을 만족하지 못한다면
stats.ttest_ind(A, B, equal_var = False)

전체적인 T검정 절차

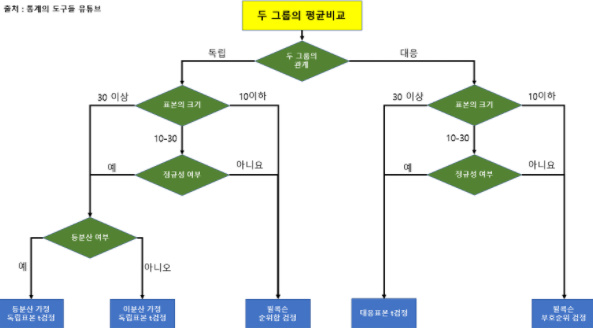
Wilcoxon's rank sum test(윌콕슨의 순위합 검정)

• 양측검정일 경우
  귀무가설 : ~와 ~은 같다.
  대립가설 : ~와 ~은 같지않다.
• 단측검정일 경우
  귀무가설 : ~와 ~은 같다.
  대립가설 : ~이 ~보다 크다

stats.ranksums(sample1, sample2)

대응표본 검정(Paired t-test)

• 두 모집단으로부터 표본을 각각 추출할 때 표본 각각의 인자가 서로 대응되는 표본

• 사전(pre)과 사후(post)를 비교할 때 주로사용한다.

• 동일한 대상 K를 새로 개발한 약물의 효과가 있는지를 알아보기 위해서는 K에게 약물을 복용하기 전과 후를 비교해야한다. 즉, 동일한 K라는 대상에게 사전(pre)과 사후(post)를 비교할때 주로 사용하는것이 있는데 이것을 대응표본(paired sample)이라고 부른다.

• 가설
  귀무가설 : 약물을 투입하기전의 몸상태의 평균과 투입후 상태의 평균이 같아.(이는 약물의 효과과 없는것으로 결론이 날 수 있다, 또한 사전(Pre)-사후(Post) = D(Difference)이며 D의 평균=0 과 같다 할 수 있다.

  대립가설 : 약물을 투입하기 전 의 평균과 투입한 후의 평균이 같지않다(D의 평균 !=0) or 약물을 투입하기 전의 평균이 한 후의 평균보다 크다(D의 평균 >0) or 약물을 투입하기 전의 평균이 후의 평균보다 작다(D의평균 <0)인 경우 이렇게 세가지로 나뉘어진다.
  

stats.ttest_rel(before, after)

대응표본 검정(Paired t-test)이 정규성 가정이 깨졌을때(정규성이 아닐때)

Wilconxon's signed rnak test(윌콕슨의 부호순위 테스트)

귀무가설 : 약물은 효과가 없다.(약물투입전 = 약물투입후)
대립가설 : 약물은 효과가 있다.(약물투입전 < 약물 투입후)

1단계 정규성 검정
2단계 Wilcoxon's signed rank test

stats.wilcoxon(before, after)
# 파라미터 zero_method, alternative
# zero_method : 같은 값을 가지는, 즉 rank-test를 함에 있어서 동일선상에 있는 관측치를 어떻게 처리할 지에 대한 방법이다.
어느 단계에서 배제하고 포함시킬 지를 결정하는 파라미터이다.