우리는 서비스를 개선시키기위해 혹은 유저경험을 개선시키기 위해서 A/B테스트를 많이 진행하게 된다.
이때 우리는 실험의 결과가 우연에 의한 차이는 아닌지 의심하게 된다.
많은 경우에 t검정을 통해서 결과에대한 최종 결정을 하게 될텐데,
t검정의 경우 몇가지 가정이 필요하다.
가장 중요한것이 정규분포를 띄어야 한다는 점이다.
실험을 하다보면 많은(?)경우에 데이터들이 아주 이쁘게 종모양의 정규분포를 띄는경우가 생각보다 많지않다.
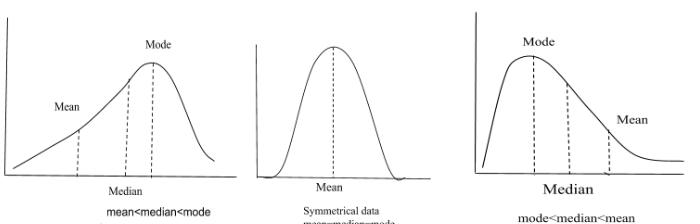
source : https://alevelmaths.co.uk/statistics/skewness/
위 사진에 보이는 것 처럼 외도가 양수 혹은 음수방향으로 치우쳐진 데이터들도 무수히 많이 보게된다.
이럴때 A/B 테스트의 결과가 우연인지, 아닌지 확인할 수 있는 방법이 바로 "부트스트랩을 통한 순열검정" 이다.
순열검정 장점
순열검정에 대한 이론적 설명을 들어가기에 앞서 "순열검정"이라는 친구는 어떤 장점을 가지고 있어서 정규분포가 아닌형태에서 t검정의 대안으로 나오는지 알아보자.
첫 번째는 실험 집단간 표본이 적고 정규성을 띄지 않는 데이터에도 검정을 시도할 수 있다는 것이다.
바로 위에서 언급한 왜도(skewness)가 있는 데이터를 처리하는데 있어서 적합할 수 있다는 것이다.(실제로 정규분포인경우 t검정과의 검정력이 상당히 유사하다는 실험들도 많다)
두번째로는 검정통계량의 결과를 시각적으로 표현할 수 있어서, 팀원들이나 다른사람들을 설득하고, 설명하는데 있어서 효과적이다.
부트스트랩을 통한 분포들의 모습을 통해서 검정결과를 설명할 수 있다.
순열검정 진행 순서
- 가설검정에 사용한 A(통제집단)와 B(실험집단)의 데이터들을 하나로 합쳐준다.
- 각각의 통제집단과 실험집단의 "갯수에 맞게" 표본을 "비복원 추출"
- A와 B의 차이를 기록한다.
- 1 ~ 3번을 N번 반복하여 검정 통계량 분포를 생성하고, 두 집단의 기존 관측값의 차이가 해당 분포 내 어느 위치에 있는지 확인한다.
주요 특징 이해하기
1.가설검정에 사용한 각 집단을 하나로 합친다는것은 통제집단과 실험집단의 차이를 두지않게다는 의미이며, 이것은 각 집단 실험 결과에 차이가 없는 동일한 그룹일 것임을 말한다. 즉, 원래 하나의 동일한 집단이 보여줄만한 분포를 만들어 실험을 통해서 나타난 관측값이 얼마나 극단에 위치할지를 확인해보는 것이다. 관측 값이 극단에 있을 수록 우연이 아님을 주장할수 있다.
2.순열(순서를바꾼다)은 집합 내 순서를 섞음으로서 기존에 관측된 순서로 인하여 발생할 수 있는 편향(bias)를 없애는것을 의미한다.
부트스트랩
순열검정시 부트스트랩 기법을 사용하여 진행하게 되는데, 이때 부트스트랩이란 "복원 추출을 N번 반복한다"라는 것과 "무작위 복원 추출"을 한다는 점을 중점으로 이해하면 된다.
우리가 A/B테스트를 하기위해 데이터로 관측한 통계량은 "표본 통계량"으로 간주된다.(모집단을 실제로 파악하기란 힘들다.) 그래서, 관측된 표본통계량을 무수히 많이 생성하는 방법을 사용하게 되는데, 이때의 통계량을 통해서 모수를 추정할 수 있게된다.
위에서 말한것 처럼 부트스트랩에서 중요한 "복원 추출을 N번반복한다"는 것은 현실에서 있을법한 또 다른 표본을 만들겠다는 의미이며, 약간의 휴리스틱한 느낌은 있습니다. 그래서 우리는 표본을 많이 만들게 되며, 그냥 복원 추출이 아닌"무작위 복원 추출" 을 통해서 각각의 데이터가 관측될 확률을 모두 독립적이고 동일하다는 가정을 만족시키기 위한 방법으로서 사용한다.
이렇게 생성된 표본의 통계량을 통해서 가장 많은 빈도로 관측된 값을 모수로 추정하고, 이값의 변동성(or불확실성)을 신뢰구간(Confidence Interval)으로 제공하는 거이다.
이떄 표본 통계량의 분포에서 표준편차가 작을수록 모수가 확실한 값이 될거고, 클수록 불확실한 값이 되는것이다. 신뢰구간은 보통 분포내의 95%로 제한하는것이 일반적인데, 표준편차의 약 2배(2sigma)정도 되는 구간으로 봐도 무방하다.(도메인에 따라 신뢰구간을 90%~99%까지 다를 수 있다.)
마찬가지로 부트스트랩 순열검정에서도 많은 검정 통계량을 생성하게되는데, 실험을 통해 얻은 차이가 이 검정 통계량 분포 내의 표준편차보다 훨씬 멀리 있다면 '우연히 관측될만한 값은 아니었어!'라고 판다할 수 있으며, 우리가 얻고싶어 하는 결론이기도 한다.
더 쉽게 풀어보면 순열검정 통계량 분포의 약 95%를 벗어난 곳에 있는 값이라면, 실험의 차이가 우연이었을 확률이 5%보다도 작다고 말할 수 있다. 그만큼 신뢰를 할 만한 차이가 있는것이다. 그리고 이것을 우리는 'p-value가 0.05이하다' 라는 것과 동일한 말로 해석할 수 있다.
분포에 따라서 비교할 통계량을 무엇으로 볼지는 조금 달라질 수 있다. 예를들어 왜도(Skewness)가 심한 분포는 평균포다 중위값을 통해서 그룹간의 차이를 비교하는게 적절할 수 있다.GPT를 활용한 부트스트랩 순열검정 test
입력한 프롬포트
부트스트랩 순열검증을 임시데이터로 한번 실험해줘
판다스로 가상의 데이터를 만들어서 웹사이트 내에서 A(처리를 하지않은)와 B(처리가이루어진)안에 대해서 각각 잔존시간에 대한 데이터를 1000개씩 만들어주고 거기에 대해서 부트스트랩 순열검정을 진행하여 P-VALUE를 산출하고, 이를 시각적으로 표현도 해줘
이때 우연에의한 차이인 경우와 실제로 차이가 있는경우 두가지로 분리해서 모두 해줘import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 임의의 데이터 생성
np.random.seed(0) # 결과의 재현성을 위해 시드 설정
group_A = np.random.normal(loc=50, scale=10, size=1000) # 평균 50, 표준편차 10의 정규분포를 따르는 데이터
group_B = np.random.normal(loc=60, scale=10, size=1000) # 평균 60, 표준편차 10의 정규분포를 따르는 데이터
# 데이터프레임 생성
df = pd.DataFrame({
'A': group_A,
'B': group_B
})
# 데이터 확인
print(df.head())
# 부트스트랩 순열 검정 함수 정의
def permutation_test(data1, data2, n_permutations=10000):
"""
순열 검정을 수행하는 함수입니다.
:param data1: 첫 번째 데이터셋 (numpy array)
:param data2: 두 번째 데이터셋 (numpy array)
:param n_permutations: 순열을 수행할 횟수
:return: p-value
"""
# 원래 데이터의 차이
observed_diff = np.abs(np.mean(data1) - np.mean(data2))
# 순열 검정을 위한 차이를 저장할 배열
perm_diffs = np.zeros(n_permutations)
# 합쳐진 데이터
combined_data = np.concatenate([data1, data2])
for i in range(n_permutations):
# 데이터를 무작위로 섞음
np.random.shuffle(combined_data)
# 섞인 데이터를 다시 두 그룹으로 나눔
perm_data1 = combined_data[:len(data1)]
perm_data2 = combined_data[len(data1):]
# 순열 데이터의 차이 계산
perm_diffs[i] = np.abs(np.mean(perm_data1) - np.mean(perm_data2))
# p-value 계산
p_value = np.mean(perm_diffs >= observed_diff)
return p_value
# 부트스트랩 순열 검정 실행
p_value = permutation_test(df['A'], df['B'])
print(f'P-value: {p_value}')
# 순열 검정 결과의 히스토그램을 그리는 함수 정의
def plot_permutation_results(data1, data2, n_permutations=10000):
"""
순열 검정 결과를 시각화하는 함수입니다.
:param data1: 첫 번째 데이터셋 (numpy array)
:param data2: 두 번째 데이터셋 (numpy array)
:param n_permutations: 순열을 수행할 횟수
"""
observed_diff = np.abs(np.mean(data1) - np.mean(data2))
perm_diffs = np.zeros(n_permutations)
combined_data = np.concatenate([data1, data2])
for i in range(n_permutations):
np.random.shuffle(combined_data)
perm_data1 = combined_data[:len(data1)]
perm_data2 = combined_data[len(data1):]
perm_diffs[i] = np.abs(np.mean(perm_data1) - np.mean(perm_data2))
plt.hist(perm_diffs, bins=30, alpha=0.7)
plt.axvline(x=observed_diff, color='red', linewidth=2)
plt.title('Permutation Test Results')
plt.xlabel('Difference in means')
plt.ylabel('Frequency')
plt.show()
# 결과 플롯
plot_permutation_results(df['A'], df['B'])
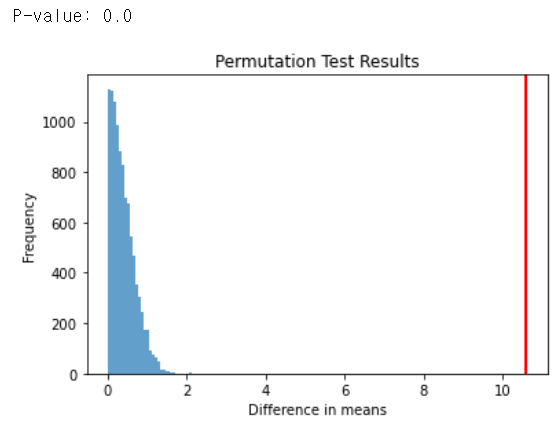
빨간색이 처리를 해준 그룹B와 그룹A의 통계량의 차이 이며, 왼쪽에 있는 파란색이 부트스트랩을 통하여 무작위 복원추출을 1만번 해서 나온 통계량을 의미합니다. 즉, 표본을 무수히 복제해서 랜덤으로 복원추출했을때의 차이랑 우리의 실험을 통해서 나온 결과의 차이는 확연하게 다릅니다. 그렇기 때문에 우리는 처리를 해준B를 채택하게 됩니다.
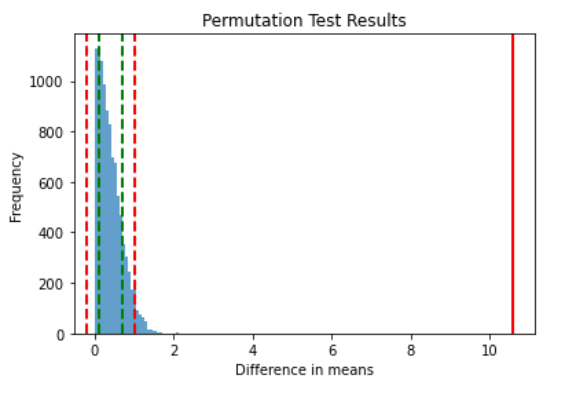
분석결과를 공유할때는
결과를 공유할때는 위 그래프보다 표준편차의 1시그마, 2시그마 범위까지 같이 표현해주면 좀 더 좋을것같습니다.