카이제곱 검정
주어진 데이터 간의 동일한 분포 혹은 빈도를 나타내는지 검정하는 방법
검정의 종류
1) 적합도 검정(Goodness of Fit test)
관찰된 비율 값이(실제값, observed)기대값(exp, expected)와 같은지 조사하는 검정(1sample 카이제곱 검정)
2) 동질성 검정
두 집단의 분포 혹은 빈도가 동일한지 검정
카이제곱을 언제 사용해야 할까??
1) Categorical데이터(질적변수)인 경우
2) 극단적인 outlier가 있는경우
3) 평균의 차이가 아닌 분포 혹은 빈도가 동일한지 검정해야할 때
즉, 요약하면 T검정의 경우 종속변수가(양적변수)이고 독립변수가(질적변수)이지만 둘다 만약 명목척도라면?? 이때는 T-test와 Anova를 사용할 수 없다. 그럴때 사용하는것이 교차분석 즉, 카이제곱 검정이다.(우리가 가진 변수가 모두 명목척도일때)
이때 주의해야 할 점은 자료의 값은 개수(count)이어야하고 교차분석이라는 점을 반드시 기억해야 한다.
| 헤드라인A | 헤드라인B | |
|---|---|---|
| 클릭 | 10 | 8 |
| 클릭하지않음 | 500 | 480 |
위의 표처럼 교차분석이고 변수들은 Categorical 해야하며 해당 자료의 값은 개수(count)이어야 한다.
카이제곱 검정 방법
- One-Sample카이제곱 검정
변수내 그룹간의 비율(proportion)이 같은지 다른지 검정하는것이다.
예를 들어 Payment method라는 변수에 4개의 범주로 구성되어있다고 가정하자(Bank transfer/ Credit card/ Electronic check/ Mailed check) 고객의 지불방법의 차이를 알고 싶을때 즉, 각 범주별로 고객의 수가 다를 이유가 없다면 정말 그런지 알고싶을때, 혹은 각 범주별로 고객의 수는 비슷할 것이라고 가정할때 사용할 수 있다.(Sapientia a Dei유튜브 영상中)
카이제곱에서는 관찰빈도(Observed)와 기대값(Expected)가 등장한다.
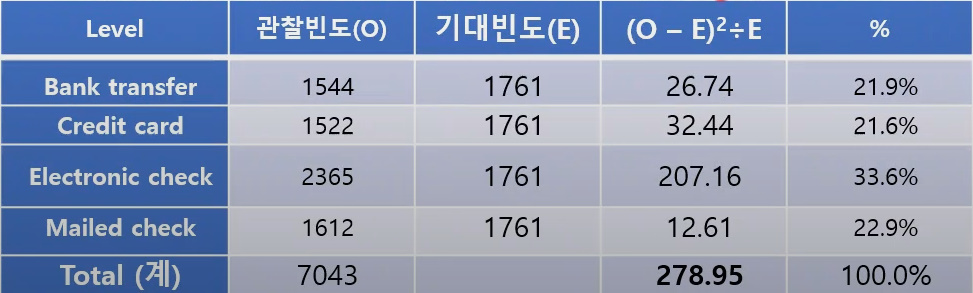
(Sapientia a Dei유튜브 영상中)
관찰빈도만 있는상태에서 기대빈도를 구해주고 보통n분의1로 한다.(도메인지식에 따라 변동이있음). 관찰빈도에서 기대빈도를 뺀것의 제곱을 다시 기대빈도로 나눈 값을 구한다.
이 값을 카이스퀘어의 통계값이라 한다.
여기서 자유도 (df)는 범주(n)-1을 해서 df = 3이된다. 여기서 나온 통계값을 p-value로 변환을 해주어야 하는데 그 식은 다음과 같다.
from scipy import stats
x2 = 278.95
pvalue = stats.chi2.cdf(x2, df = 3)
pvalue< 0.05(기준)즉, 일원카이제곱에서 검정의 유의성이 의미하는것은 범주들이 뭔가 다르다는 것 정도인다.
여기서 다르다는 것은 사전에 정해진 기대빈도와 다르다는 의미이다.
scipy에서 일원 카이제곱
# 어레이 생성
from scipy.stats import chisquare
obs = np.array([[56],[1454],[1216],[80]])
chi2 = chisquare(obs, axis = None)
chi2
>>> Power_divergenceResult(statistic=2329.1503920171062, pvalue=0.0)
# 관측값은 서로 관련이 없다.- Two-Sample카이제곱 검정
변수 사이의 연관성(Association)이 있는지 없는지 검정하는것이다.
이 명목척도는 2개 이상의 범주(category)를 가진다.
변수가 두 개 이므로 데이터 코딩시 두 개의 컬럼에 코딩한다.
가장 단순한 형태는 2 x 2분석이다.
이때 사용하는 것이 분할표(contingency table)이다.
여기서 분할표란 데이터의 빈도만 단순화된 표에 작성하는것을 말하며 두개의 변수를 행(Raw)과 열(Column)으로 나누어 빈도를 정리한다.
이 분할 표를 통해 이원 카이제곱 검정을 하는 목적은 행과 열 사이에 (즉 두 변수 사이에) 어떠한 연관성이 있는지 확인해보는 것이다.
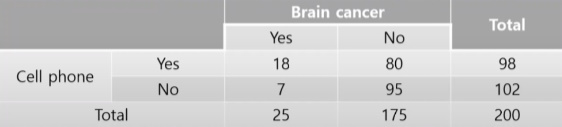
(Sapientia a Dei유튜브 영상中)
휴대폰 사용에 따른 뇌암의 대한 빈도를 다룬 분할표 이다.
여기서 Brain cancer환자의 72%가 진단전에 3년이상 cell phone을 사용했다
- P(CP|BC) = 18 / 25 = 0.72 (P는 확률이고 , 뒤에 기호는 뒤에조건이 있을때 앞의 조건 즉, Brain cancer일때 Cell phone을 사용한것)
다른 암 환자의 46%가 진단 전에 3년이상 cell phone을 사용했다.
- P(CP|NBC) = 80 / 175 = 0.46
카이제곱 검정안했는데 72프로가 46프로보다 더 높다하지만 더 확실히 하기위해 카이제곱검정을 해본다.
목적: brain cancer와 cell phone사용 간의 연관성(association)확인(인과관계가 아니다, 그냥 연관성이다)
통계적 가설
- H0 = brain cancer와 cell phone사용 간에는 연관성이 없다.(상호 독립이다)
- Ha = brain cancer와 cell phone 사용 간에는 연관성이 있다.
기대빈도 계산법 = (행 합계) x (열 합계) / (총 합계)
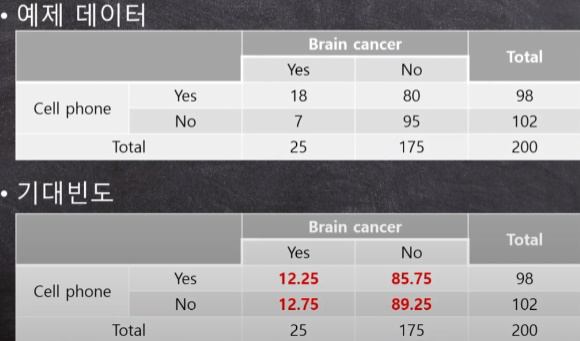
이것을 카이제곱 해보면 나온다.
scipy에서 이원 카이제곱 검정 하기
# 귀무가설 : 두 변수간 연관이 없다.
# 대립가설 : 두 변수간 연관이 있다.
from scipy.stats import chi2_contingency
obs = np.array([5,4,3,2])
chi2_contingency(obs)검정결과 해석 -> 1.카이제곱 통계량, 2. P-value, 3.degree of freedom, 4. 기대값
