[혼자 공부하는 ML+DL] #2 - 회귀 알고리즘과 모델 규제

본 내용은 한빛미디어의 [혼자 공부하는 머신러닝+딥러닝]을 참고하였습니다.

---

Chapter 03. 회귀 알고리즘과 모델 규제

03-1. KNN 회귀

• 회귀? -> 변수 사이의 상관관계를 분석해 임의의 어떤 숫자를 예측
• KNN 회귀 : 근접한 이웃 k개의 타깃값의 평균으로 예측 타깃값을 결정

  KNeighborsRegressor : KNN 회귀 모델을 만드는 scikit-learn 클래스

** numpy reshape : 배열의 크기를 바꿀 때 사용하는 메서드, 원본 배열에 있는 원소의 개수를 맞춰야함

test_array=np.array([1,2,3,4])
test_array=test_array.reshape(2,2) #(4,) --> (2,2)

• 결정계수($R^2$)
  -> KNN 분류에서 score = 정확하게 분류한 개수의 비율
  -> 회귀의 경우 score = 결정계수($R^2$)로 판단

  $R^2 = 1 - (타깃-예측)^2/(타깃-평균)^2$

  ** mean_absolute_error : 타깃과 에측의 절댓값 오차를 평균하여 반환

from sklearn.metrics import mean_absolute_error
 test_prediction = knr.predict(test_input)
 mae = mean_absolute_error(test_target, test_prediction)

• 과대적합 : 모델의 훈련 세트 성능이 테스트 세트 성능보다 너무 좋아서 데이터에 내재된 거시적인 패턴을 감지하지 못함

• 과소적합 : 훈련 세트와 테스트 세트 성능이 모두 낮거나 테스트 세트 성능이 오히려 더 높아서 모델이 적절히 훈련되지 못함
  ** 과소적합 해결방법 : 더 복잡한 모델을 사용해야함( ex - knn에서 k의 개수를 줄임)

03-2. 선형 회귀

• 선형 회귀 : 특성과 타깃 사의의 관계를 가장 잘 나타내는 선형 방정식을 찾음. 특성이 하나면 직석 방정식이 하나.

  LinearRegression : 선형 회귀 모델을 만드는 scikit-learn 클래스

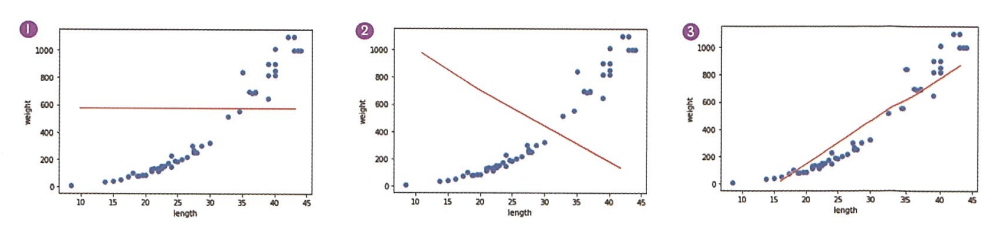  그래프 1. 데이터를 하나로 예측 -> 직선의 위치가 훈련 세트의 평균이라면 $R^2=0$
  그래프 2. 완전히 반대로 예측 -> $R^2 < 0$
  그래프 3. 가장 잘 예측한 직선 -> $R^2$이 1에 가까운 값

• 계수, 가중치 : 선형 회귀가 찾은 특성과 타깃 사이의 관계는 선형 방정식의 계수 또는 가중치에 저장됨. 보통 가중치는 방정식의 기울기아 절편 모두를 의미함

print(lr.coef_, lr.intercept_) # 기울기(특성의 계수)와 절편 확인

• 다항 회귀 : 다항식을 사용하여 특성과 타깃 사의의 관계 확인. 곡선처럼 비선형일 수 있지만 여전히 선형 회귀로 표현할 수 있음.

  Ex) $무게 = 1.01 \times 길이^2 - 21.6 \times 길이 + 116.05$
  --> 모델이 학습한 그래프라 할때, $길이^2$을 '왕길이'와 같은 다른 변수로 치환하면 무게는 왕길이와 길이의 선형 관계로 표현할 수 있음.

03-3. 특성 공학과 규제

• 다중 회귀 : 여러 개의 특성을 사용헌 선형 회귀

  1번 그림은 1개의 특성을 사용한 선형 회귀, 2번 그림은 2개의 특성을 사용한 다중회귀.

• 특성 공학 : 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업

• pandas : 데이터프레임을 사용하는 데이터 분석 라이브러리

import pandas as pd #pandas 라이브러리 불러오기
df = pd.read_csv('https://bit.ly/perch_csv') #데이터 읽어오기
perch_full = df.to_numpy() #읽어온 데이터를 numpy형태로 변환

• 변환기 : 사이킷런에서 특성을 만들거나 전처리하기 위해 제공하는 클래스

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(include_bias=False)
poly.fit([[2,3]]) #새롭게 만들 특성 조합을 찾음([2,3,4,6,9] ->특성의 제곱과 특성끼리의 곱)
poly.transform([[2,3]]) #실제로 데이터를 변환

• 다중 회귀에서의 과대적합 : 특성의 개수를 너무 늘리면 훈련 세트에 대해 너무 완벽하게 학습하여 과대적합되고, 테스트 세트에서는 형편없는 점수를 만듦

• 규제 : 과대적합되지 않도록 훼방하는 것. 선형 회귀의 경우 특성에 곱해지는 계수(or 기울기)의 크기를 작게 만드는 일. 선형 회귀 모델에 규제를 추가한 모델 -> 릿지, 라쏘

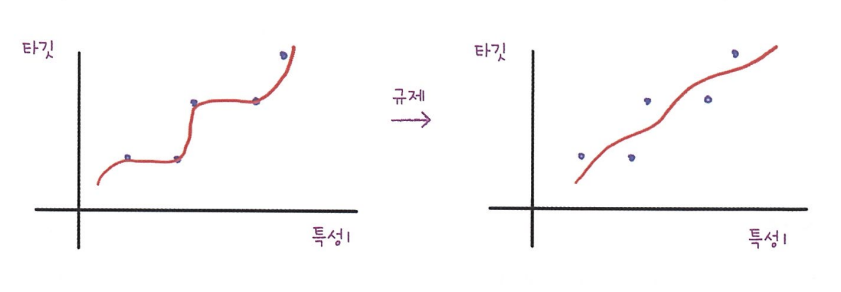  왼쪽 그림은 과대적합된 경우, 오른쪽 그림은 이를 방지하기 위하여 기울기를 줄인 경우.

• 릿지 회귀 : 선형 모델의 계수를 작게 만들어 과대적합을 완화시킴.

from sklearn.linear_moder import Ridge
ridge = Ridge()
ridge.fit(train_scaled, train_target) 

하이퍼파라미터 : 머신 러닝 모델이 학습할 수 없고 사람이 알려줘야 하는 파라미터. 릿지 모델에서는 alpha 매개변수를 나타내고 이 변수로 규제의 강도를 조절함.

• 적절한 alpha값 찾기
  -> alpha값에 대한 $R^2$값의 그래프 그려보고 훈련 세트와 테스트 세트의 점수가 가장 가까운 지점을 찾아야함.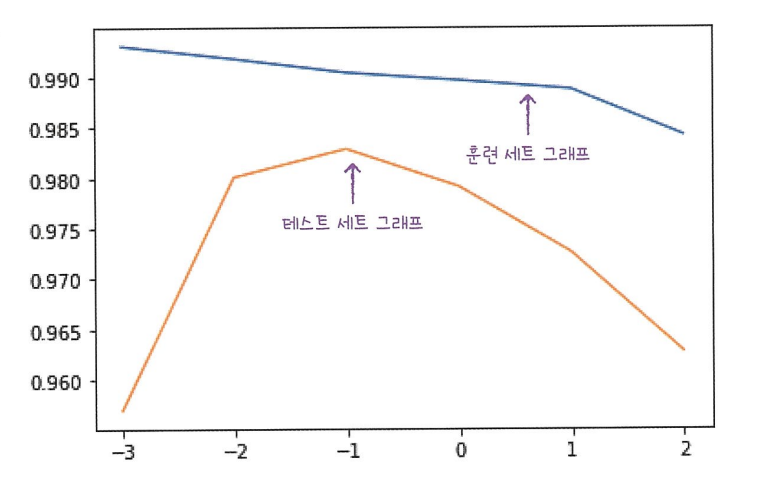

  위의 그래프는 score값에 자연로그를 취한 그래프임. 적절한 alpha값은 -1부분 즉, alpha = 0.1

• 라쏘 회귀 : 또 다른 규제가 있는 선형 회귀 모델. 릿지와 달리 계수 값을 아예0으로 만들 수도 있음.

from sklearn.linear_moder import Lasso
lasso = Lasso()
lasso.fit(train_scaled, train_target)