Defi
CPMM
CPMM 은 constant product market makers 의 약자이다.
uniswap 에서 처음 제시한 함수로, 토큰 스왑 거래를 지원하기 위해 도입했다.
유니스왑은 X * Y = K 수식으로 풀을 설명할 수 있다.
X 토큰의 갯수, Y 토큰의 갯수가 K 인 풀의 크기를 결정한다.
CPMM 함수
흔히 x*y = k로 정의되며 위 함수는 거래가 발생하는 시점의 함수를 정의한 모습이다.
여기서 R은 리저브를 의미하며 R_a와 R_b는 교환 대상이 되는 두 토큰이다.
γ는 트랜잭션 수수료이며 k를 유지하기 위한 변화량이 각 풀 내 리저브양에 더해지고 감소한다.
두 토큰 리저브 수량의 곱이 항상 일정한 k를 유지해야 하기 때문에 토큰의 가격은 토큰 수량의 반비례 그래프를 형성한다.
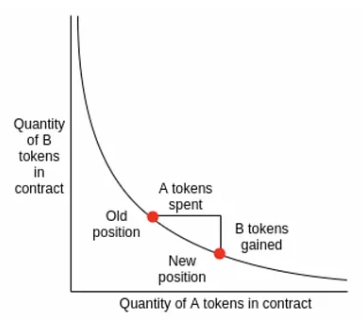
이러한 반비례 그래프를 형성한다.
CPMM 은 두 가지의 특징이 있다.
- 먼저 교환하고자 하는 토큰 수량이 많을수록 더 큰 손해를 보게된다.
이를 전문용어로는 슬리피지(Slippage)라고도 표현한다.
오더북에서는 판매자만 있다면 내가 원하는 가격에 원하는 양만큼 구입할 수 있지만 CPMM에서는 원하는 가격에 구매할 수 없다. 다시 말해서 Limit Order를 할 수 없고 시장가로 다 긁어야 한다.
- 반비례 그래프 특성상 양쪽으로 무한히 발산하기 때문에 이론상 무한대의 유동성(Infinite Liquidity)을 제공한다. 풀 내에 유동성만 예치되어 있다면 구매자는 항상 상품을 구입할 수 있다.
반면, 오더북 기반 거래소에서는 팔고 싶어도 구매자가 없어 팔지 못하는 상황이 연출될 수 있다.
CPMM in solidity
위의 링크에서 유니스왑의 CPMM 에 대해 읽어보았으나, 역시 어려웠다.
그래서 수업시간 중 배운 CPMM 컨트랙트 코드를 다시 보았다.
코드는 아래와 같다.
function balanceOfAB() public view returns(uint, uint) {
return (token_a.balanceOf(address(this)), token_b.balanceOf(address(this)));
}
// 공급
function provideLiquidity(address _token, uint _a) public isitAorB(_token) {
(uint bal_a, uint bal_b) = balanceOfAB();
uint mint_lp;
if(_token == address(token_a)) {
uint _b = _a * bal_b / bal_a;
token_a.transferFrom(tx.origin, address(this), _a);
token_b.transferFrom(tx.origin, address(this), _b);
mint_lp = _a * totalSupply() / bal_a;
} else {
uint _b = _a * bal_a / bal_b;
token_a.transferFrom(tx.origin, address(this), _b);
token_b.transferFrom(tx.origin, address(this), _a);
mint_lp = _a * totalSupply() / bal_b;
}
// lp 토큰 지급
_mint(msg.sender, mint_lp);
// k = (bal_a + _a) * (bal_b + _b) ;
}먼저, balanceOfAB() 함수로 현재의 풀을 운영하고 있는 컨트랙트가 가지고 있는 A,B 토큰의 비율을 가져온다.
예치할 A 토큰을 입력하면, 자동으로 B 토큰을 계산하는데, 방금 가져온 A, B 토큰 비율로 예치할 B 토큰을 계산한다.
uint _b = _a * bal_b / bal_a;
반대로, 예치할 B 토큰을 입력하면, 자동으로 A 토큰을 계산하며, 현재 풀의 A, B 토큰 비율로 예치할 A 토큰을 계산한다.
uint _b = _a * bal_a / bal_b;
그리고 A, B 토큰을 예치하며 풀에 유동성을 공급한 사람에게 LP(liquidity pool) 토큰을 지급한다.
풀에 예치한 A, B 토큰을 찾아갈 때는 이때 받은 LP 토큰 만큼을 반납해야 출금 받을 수 있다.
풀에 유동성을 공급하는 함수를 만들었으니, 반대로 유동성을 회수하는 함수도 만들어야 한다.
// 제거
function withdrawLiquidity(uint _a) public {
require(balanceOf(msg.sender) >= _a, "not enough");
(uint bal_a, uint bal_b) = balanceOfAB();
// lp 토큰 수령 후 확인
uint a_out = _a * bal_a / totalSupply();
uint b_out = _a * bal_b / totalSupply();
token_a.transfer(msg.sender, a_out);
token_b.transfer(msg.sender, b_out);
// k = (bal_a - _a) * (bal_b - _b);
}먼저, balanceOfAB() 함수로 현재의 풀을 운영하고 있는 컨트랙트가 가지고 있는 A,B 토큰의 비율을 가져온다.
그리고 유동성 공급 시 지급하였던 LP 토큰을 회수한다.
회수가 확인되면 현재 풀에 남아있는 A,B 토큰을 총 공급량으로 나누어 A, B 토큰을 지급한다.
uint a_out = _a * bal_a / totalSupply();
uint b_out = _a * bal_b / totalSupply();
이때, K(풀의 크기) 는 K = X * Y 공식에 따라, (bal_a - _a) * (bal_b - _b) 로 변화할 것이다.
다음은 거래이다.
A 또는 B 토큰 일정량을 가져와서 다른 토큰으로 교환한다고 했을 때, 아래의 코드대로 실행된다.
// 거래
function swapToken(address _token, uint _amount) public isitAorB(_token) {
(uint bal_a, uint bal_b) = balanceOfAB();
uint k = bal_a * bal_b;
if(_token == address(token_a)) {
uint out = bal_b - k / (bal_a + _amount);
token_a.transferFrom(tx.origin, address(this), _amount);
token_b.transfer(msg.sender, out);
} else {
uint out = bal_a - k / (bal_b + _amount);
token_b.transferFrom(tx.origin, address(this), _amount);
token_a.transfer(msg.sender, out);
}
}먼저, 풀의 A ,B 비율을 가져온다.
(uint bal_a, uint bal_b) = balanceOfAB();
가져온 비율로 K(풀의 크기) 를 정의해준다.
uint k = bal_a * bal_b;
가져온 토큰을 확인하고, 받아갈 토큰B 에 대한 수식을 작성한다.
uint out = bal_b - k / (bal_a + _amount);
수식에 따라 토큰을 회수한다.
token_a.transferFrom(tx.origin, address(this), _amount);
아까 보았던 반비례 그래프다.
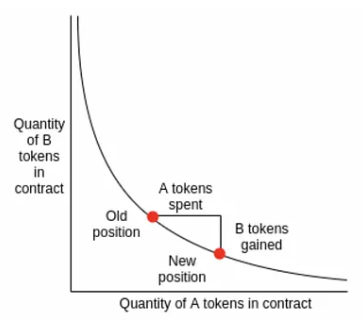
유동성 풀에 유동성을 공급, 회수 할때는 이 그래프가 Y 축을 기준으로 위아래로 움직이게 되고,
A 토큰을 B 토큰으로 스왑했을 경우에는 X 축을 기준으로 오른쪽으로.
B 토큰을 A 토큰으로 스왑하는 경우엔 X 축 기준으로 왼쪽으로 이동하게 된다.
