[알고리즘] 순열 조합 부분집합 정리

완전 탐색 문제 중 재귀의 기본이 되는 순열 조합 부분집합에 대한 예시 코드 및 이론 정리

순열 (Permutation)

• 서로 다른 것들 중 몇개를 뽑아서 한 줄로 나열하는 것
• 서로 다른 n 개 중 r 개를 택하는 순열은 아래와 같이 표현한다.
  • $nPr$
• $nPr$ 은 아래와 같은 식이 성립한다.
  • $nPr = n * (n-1)* (n-2) * ... * (n-r+1)$
• $nPn = n!$ 이라고 표기하며 팩토리얼(Factorial) 이라고 한다.
• 다수의 알고리즘 문제들은 순서화된 요소들의 집합에서 최선의 방법을 찾는 것과 관련 있음
• N 개의 요소들에 대해, n! 개의 순열들이 존재함

순열 구현 (재귀 예시)

int n;		// 숫자의 개수
int[] num;	// 뽑은 숫자 배열
int[] arr;	// 뽑을 숫자 배열
boolean[] used;	// 방문 배열

public void permutation(int depth, int n) {
	if (depth == n) {
    	System.out.println(Arrays.toString(num));
        return;
    }
    
    for (int i = 0; i < n; i++) {
    	if (used[i]) {
        	continue;
        }
        num[depth] = arr[i];
        used[i] = true;
        permutation(depth + 1, n);
        used[i] = false;
    }
}

중복 순열 구현 (재귀 예시)

중복 순열은 방문 여부를 확인 할 필요가 없으므로, 순열을 구하는 코드에서 방문 배열 관련 코드를 제거하면 된다.

int n;		// 숫자의 개수
int[] num;	// 뽑은 숫자 배열
int[] arr;	// 뽑을 숫자 배열

public void permutation(int depth, int n) {
	if (depth == n) {
    	System.out.println(Arrays.toString(num));
        return;
    }
    
    for (int i = 0; i < n; i++) {
        num[depth] = arr[i];
        permutation(depth + 1, n);
    }
}

조합 (Combination)

• 서로 다른 n 개의 원소 중 r 개를 순서 없이 골라낸 것
• 조합의 수식
  

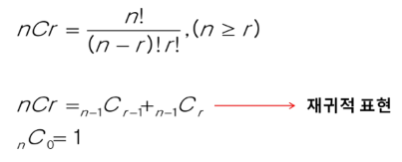
구현 (재귀 예시)

조합의 경우는 순열과 다르게 중복체크가 따로 필요없다. 호출하는 부분에서 i+1 로 값을 전달하기 때문에, 현재 값이 다시 사용되지 않는다.

int n;		// 숫자의 개수
int[] num;	// 뽑은 숫자 배열
int[] arr;	// 뽑을 숫자 배열

public void combination(int depth, int now, int n) {
	if (depth == n) {
    	System.out.println(Arrays.toString(num));
    }
    
    for (int i = now; i < n; i++) {
    	num[depth] = arr[i];
        combination(depth+1, i+1);
    }
}

중복조합 구현 (재귀 예시)

중복 조합의 경우는 기존 조합 코드에서 단 한줄의 일부만이 달라진다.
중복 순열의 경우와 동일하게 중복체크 관련 부분이 달라진다.

int n;		// 숫자의 개수
int[] num;	// 뽑은 숫자 배열
int[] arr;	// 뽑을 숫자 배열

public void combination(int depth, int now, int n) {
	if (depth == n) {
    	System.out.println(Arrays.toString(num));
    }
    
    for (int i = now; i < n; i++) {
    	num[depth] = arr[i];
        combination(depth+1, i);	// 여기
    }
}

부분집합 (Subset)

• 집합에 포함된 원소들을 선택하는 것
• 다수의 중요 알고리즘들이 원소들의 그룹에서 최적의 부분 집합을 찾는 것

부분집합의 수

• 집합의 원소가 n개일 때, 공집합을 포함한 부분집합의 수 : $2^n$ 개
• 각 원소를 부분집합에 포함시키거나 그러지 않는 2가지 경우를 모든 원소에 적용한 수와 같음

부분집합 구현 (재귀 예시)

int n;			// 숫자의 개수
int[] arr;		// 뽑을 숫자 배열
boolean[] used;	// 방문배열

public void subset(int depth, n) {
	if (depth == n) {
    	for (int i = 0; i < n; i++) {
        	if (used[i]) {
            	System.out.println(arr[i] + " ");
            }
    	}
        System.out.println();
        return;
    }
    
    // 현재 위치의 숫자를 선택한 경우의 부분집합을 구함
    used[depth] = true;
    subset(depth+1, n);
    
    // 현재 위치의 숫자를 선택하지 않은 경우의 부분집합을 구함
    used[depth] = false;
    subset(depth+1, n);
}