[알고리즘] 에라토스테네스의 체

<이미지 출처: 위키 백과>

에라토스테네스의 체 이론

에라토스테네스의 체는 솔직히 간단한 알고리즘이다.
소수가 되는 수의 배수를 지우면, 남은 모든 수는 소수가 된다. 라는 아이디어의 알고리즘이다.

아래는 위키백과에 나온 과정 설명이다.
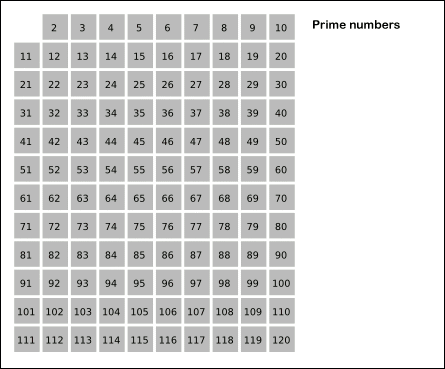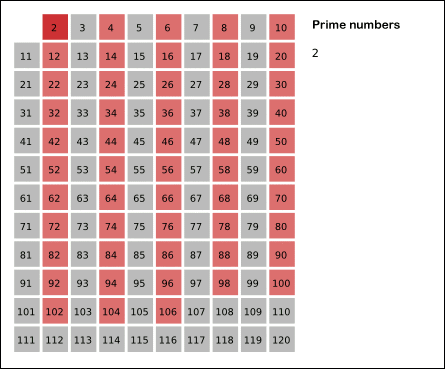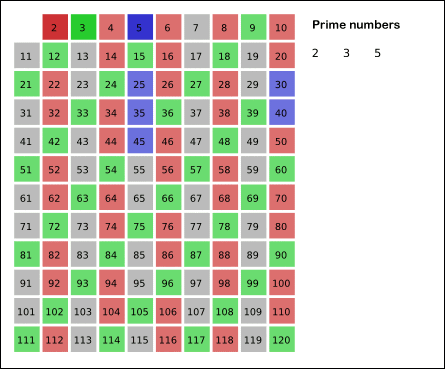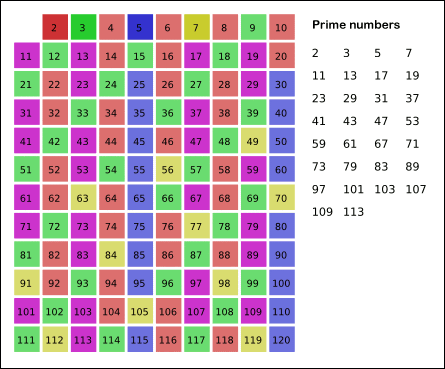
1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다.
2. 소수가 되는 수의 배수를 지우면 남은 것은 소수이다.
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 중 3은 소수이므로, 오른쪽에 3을 쓴다.
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아 있는 수 중 5는 소수이므로, 오른쪽에 5를 쓴다.
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
8. 1 ~ 7 과정을 반복한다.

이제 이해가 되었다면, 일반적인 소수 판별 알고리즘과 함께 코드를 확인해보자.

일반적인 소수 판별 구현

일반적인 소수 판별의 시간 복잡도는 $O(N)$ 으로, N 개의 수를 판별하면 $O(N^2)$ 이다.

public boolean isPrime(int n) {
	if (n < 2) return false;
	for (int i = 2; i * i <= n; i++) {
		if (n % i == 0) return false;
	}
	return true;
}

에라토스테네스의 체 구현

시간 복잡도는 $O(N loglogN)$ 으로 일반적인 소수 판별보다 빠른 속도로 동작한다.

boolean[] isPrime;
public void isPrime(int n) {
	isPrime = new boolean[n+1];
    
    // boolean 배열의 default 는 false 이므로 모두 true 로 초기화
    // 0 과 1은 확인할 필요 없으므로 그대로 false 로 두기 위해 2부터 반복시작
    for (int i = 2; i < n; i++) {
    	isPrime[i] = true;
    }
    
    // 2부터 n의 제곱근 숫자까지의 모든 수 확인
    for (int i = 2; i <= Math.sqrt(n); i++) {
    	// 현재 수가 소수라면, 해당 수를 제외한 배수들을 모두 false 로 처리
    	if (isPrime[i]) {
        	// i * i 이하의 수는 모두 검사했으므로, i * i 부터 시작
        	for (int j = i * i; j <= n; j += i) {
            	isPrime[j] = false;
            }
        }
    }
}