[알고리즘] 최장 증가 부분 수열(LIS, Longest Increasing Subsequence)

최장 증가 부분 수열(LIS)

개념

원소가 n개인 배열의 일부 원소를 골라만든 부분 수열 중 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열

• 예를 들어, { 6, 2, 5, 1, 7, 4, 8, 3} 이라는 배열이 있을 경우, LIS는 { 2, 5, 7, 8 }
• { 2, 5 }, { 2, 7 } 등 증가하는 부분 수열은 많지만 그 중에서 가장 긴 것이 { 2, 5, 7, 8 }

일반적으로 LIS 의 길이가 얼마인지 푸는 간편한 방법은 DP를 이용하는 것

구현

• 예시 코드 아래에서 length[i] 는 i 번째 인덱스에서 끝나는 최장 증가 부분 수열의 길이 를 의미함

  int max = 0;
  for (int i = 0; i < N; i++) {
  	LIS[i] = 1; // 자신만 끝에 세울 경우 1의 길이
  	for (int j = 0; j < i; j++) {
  		if (arr[j] < arr[i]) {
  			LIS[i] = Math.max(LIS[i], LIS[j] + 1);
  		}
  	}
  	max = Math.max(max, LIS[i]);
  }

  • 주어진 배열에서 인덱스를 한 칸씩(i++) 늘려가면서 확인
  • 내부 반복문으로 i보다 작은 인덱스들을 하나씩 살펴보면서 arr[j] < arr[i] 인 것이 있을 경우, LIS[i] 를 업데이트함
  • 업데이트 기준

    1. j 번째 인덱스에서 끝나는 LIS의 마지막에 arr[i] 를 추가했을 때의 LIS 의 길이

    2. 추가하지 않은 기존의 LIS[i] 의 값

       1 과 2 중 더 큰 값으로 LIS[i] 의 값을 업데이트

---

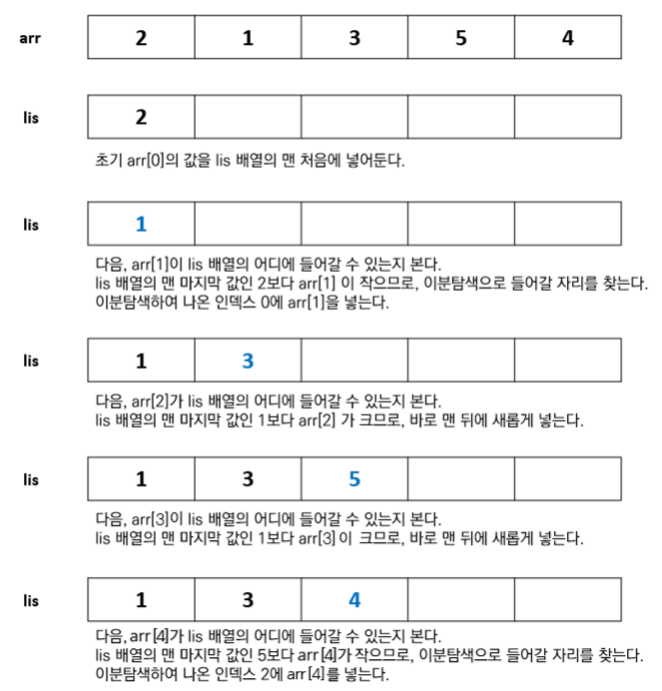
이진탐색 사용

시간복잡도 개선을 위해 LIS 구성 시 이진탐색을 활용

LIS 의 형태를 유지하기 위해 주어진 배열의 인덱스를 하나씩 살펴보면서 그 숫자가 들어갈 위치를 이진탐색으로 탐색해서 넣음

구현

• 예시코드

  int size = 0;
  for (int i = 0; i < N; i++) {
  	// 이진 탐색을 통해 삽입 위치 탐색
  	int idx = Arrays.binarySearch(LIS, 0, size, nums[i]);
  	idx = Math.abs(idx) - 1;
  	// idx 자리에 값 갱신 : 0 번부터 idx 번까지 원소 개수가 idx 위치에 저장된
  	// 그 값을 마지막으로 하는 LIS 길이가 됨
  	// 배열의 원소가 LIS를 이루는 구성 요소와는 관계가 없음
  	LIS[idx] = nums[i];
  	
  	if (size == idx) {
  		size++;
  	}
  }

시간 복잡도

• 이진탐색 미사용 : $O(N^2)$
• 이진 탐색 사용: $O(Nlog N)$