문제
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는
((n-1) * n) / 2이하입니다. - 임의의 i에 대해, costs[i][0] 와 costs[i][1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i][2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
- 연결할 수 없는 섬은 주어지지 않습니다.
입출력 예시
| n | costs | return |
|---|---|---|
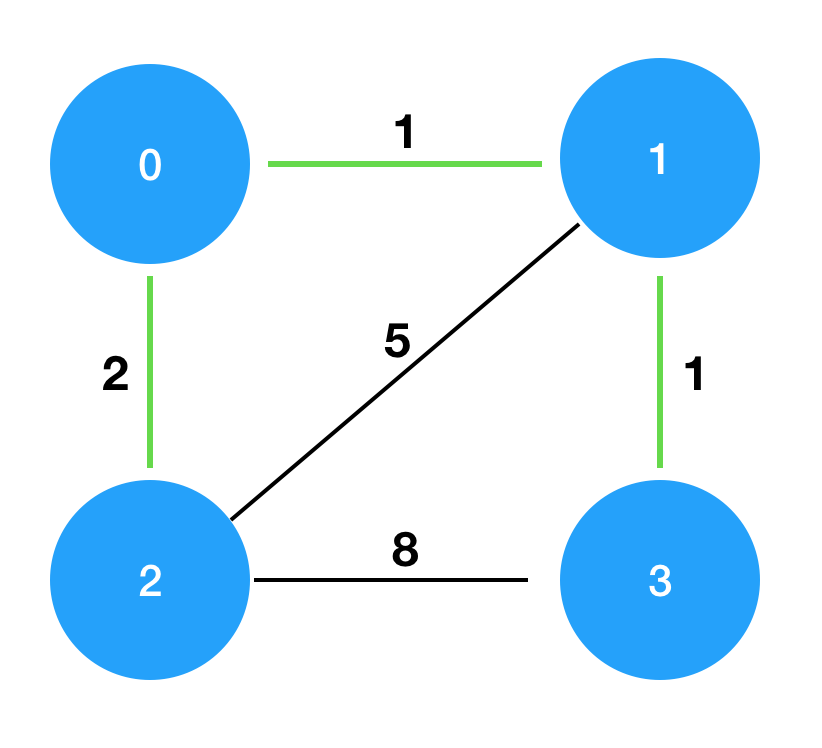
| 4 | [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] | 4 |
풀이
Greedy 카테고리에 있는 문제이면서 동시에 그래프문제이다. 그래프 문제는 출제 측에서 의도적으로 해법을 단 하나의 접근 방법으로 고정하지 않는 이상 다양한 알고리즘을 적용해서 풀 수 있다. (물론 다른 알고리즘도 마찬가지겠지만;)
다시 본론으로 돌아와서 해당 문제는 최소 비용 신장 트리(MST)를 구하는 것과 동일하다. 문제 조건에 의해 연결할 수 없는 섬이 주어지지 않으며, 모든 섬이 연결되어야 하므로 이 경우 간선의 수는 그래프에 있는 노드의 수 - 1과 같다. 즉 최소 비용의 간선을 노드의 수 - 1개 만큼 선택하여 트리를 구성해야 한다.
MST를 구하는 알고리즘 역시 여러개가 있으나, 해당 풀이에서는 그루스칼(Kruskal) 알고리즘을 적용하여 풀어보겠다. 그루스칼 알고리즘은 Greedy 알고리즘 이기도 하다. 기본적으로 해당 알고리즘은 주어진 간선들의 가중치를 보고 사이클 여부를 체크하면서 항상 최대/최소 가중치만 선택하기에 Greedy 접근이 가능하다.
그루스컬 알고리즘을 구현할 때 그 내부는 또 다시 Union-Find라는 개념을 사용한다. Union-Find 알고리즘은 여러 개의 노드가 있을 때 선택된 두 개의 노드가 현재 같은 그래프에 있는지를 판별한다. 따라서 그루스칼 알고리즘에서 Union-Find를 이용하여 사이클을 체크하는 것이다.
그렇다면 먼저 베이스가 되는 Union-Find 알고리즘 부터 구현해보자.
// union-find의 가장 핵심 로직이다.
// x의 Parent를 찾는 함수며 재귀로 구현했다.
// 처음에 parent 배열은 각자 자기 자신을 부모로 갖고 있다.
// 만약 두 노드가 연결되어 있다면 두 개의 노드를 모두 동일한 부모로 변경해야 할 것이다.
// 일반적으로 더 작은 노드값으로 부모값을 지정한다.
// x의 parent가 자기 자신이 아닐 경우,
// 다음 x는 x의 parent 값(= parent[x])로 전달하여
// 계속해서 상위(= 여기선 더 작은 노드)로 탐색한다.
const getParent = (parent, x) => {
if(parent[x] === x) return x;
return parent[x] = getParent(parent, parent[x]);
}
// getParent 함수만 이해하면 어렵지 않다.
// 두 노드의 부모를 병합(union)하는 과정이다.
// 위에서 언급했듯, 더 작은 값을 가진 노드의 번호로 부모를 병합하고 있다.
const unionParent = (parent, a, b) => {
const n1 = getParent(parent, a);
const n2 = getParent(parent, b);
if(n1 < n2) return parent[n2] = n1;
else return parent[n2] = n1;
}
// 역시 getParent 함수를 이해하면 어렵지 않다.
// 두 노드의 부모를 찾아주고,
// 두 노드의 부모가 같으면 true, 아니면 false를 반환한다.
const findParent = (parent, a, b) => {
const n1 = getParent(parent, a);
const n2 = getParent(parent, b);
if(n1 === n2) return true;
else return false;
}getParent() 함수만 이해한다면 전체 로직을 이해하기는 크게 어렵지 않다. 다시 한번 getParent 함수가 재귀적으로 동작하고, 만약 연결된 노드들일 경우 그 중에서 가장 상위에 있는 부모 노드를 가져오는 함수라는 것을 잘 기억하자!
Union-Find 알고리즘을 구현했으니 이를 이용하여 그루스칼 알고리즘을 구현해보자. 먼저 그루스칼 알고리즘은 Greedy 하게 동작한다고 설명했다. 때문에 우리가 필요한 간선은 최소 가중치를 가진 간선이므로 먼저 간선을 기준으로 오름차순 정렬을 해준다.
costs.sort((a,b) => a[2] - b[2]);또한 기본적으로 parent 배열 초기화가 필요하다. 앞에서도 말했듯 초기 상태의 parent 배열은 각자 자기 자신이 동시에 부모인 상태이다. 즉 노드가 1, 2, 3, 4, 5 총 5개가 있을 때, 초기 parent 배열의 값은 [1, 2, 3, 4, 5] 가 될 것이며 이는 각각 첫 번째 노드(parent[0])의 부모는 1이라는 것과 같다.
// 자기 자신의 값으로 parent 배열 초기화
const parent = [];
for(let i = 0; i < n; i++)
parent.push(i);이제 이 두 가지를 가지고 앞서 구현한 Union-Find를 이용해 그루스칼 알고리즘을 구현할 수 있다. 우리는 앞서서 최소 가중치를 기준으로 정렬했기 때문에 순차적으로 접근하며 두 개의 노드가 연결되어 있지 않다면 연결하고 그 간선의 가중치를 더해줄 것 이다. 그리고 이후 두 개의 노드는 서로 연결되었기 때문에 병합(union)해주면 된다.
for(const cost of costs) {
if(!findParent(parent, cost[0], cost[1])) {
answer += cost[2];
unionParent(parent, cost[0], cost[1]);
}
}주석을 제외한 전체 코드는 다음과 같다.
코드
const getParent = (parent, x) => {
if(parent[x] === x) return x;
return parent[x] = getParent(parent, parent[x]);
}
const unionParent = (parent, a, b) => {
const n1 = getParent(parent, a);
const n2 = getParent(parent, b);
if(n1 < n2) return parent[n2] = n1;
else return parent[n1] = n2;
}
const findParent = (parent, a, b) => {
const n1 = getParent(parent, a);
const n2 = getParent(parent, b);
if(n1 === n2) return true;
else return false;
}
function solution(n, costs) {
let answer = 0;
const parent = [];
for(let i = 0; i < n; i++)
parent.push(i);
costs.sort((a, b) => a[2] - b[2]);
for(const cost of costs) {
if(!findParent(parent, cost[0], cost[1])) {
answer += cost[2];
unionParent(parent, cost[0], cost[1]);
}
}
return answer;
}출처
https://programmers.co.kr/learn/courses/30/lessons/42861?language=javascript

