문제
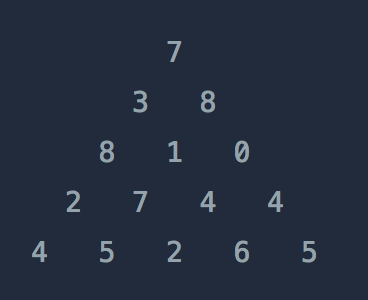
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
제한
- 삼각형의 높이는 1 이상 500 이하입니다.
- 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
입출력 예시
| triangle | result |
|---|---|
| [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] | 30 |
풀이

해당 문제 역시 프로그래머스에서 JS로 풀 수 없다. JS가 알고리즘 풀이에서는 주류 언어가 아니고, 더구나 옛날 문제일 수록 JS를 지원하지 않도록 설계되었기 때문에 그런 것 같다. 최근 문제들은 대부분 JS를 지원하고 있다. JS Lover로서 역시 해당 문제를 JS로 풀어보자!
역시 DP를 적용하여 푸는 문제다. 탑-다운(Top-Dowm) 또는 바텀-업(Bottom-UP) 방식 중에 하나를 선택해서 풀 수 있다. 해당 풀이에서는 바텀-업 방식으로 접근해보려 한다.
밑에서 부터 위로 접근을 하게 되면 다음과 같이 생각할 수 있다.
- 현재 라인 특정 값의 좌표를 dp[i][j]라고 하자.
- dp[i][j]는 dp[i+1][j]와 dp[i+1][j+1]로 접근할 수 있다.
- 거꾸로 생각하면 dp[i+1][j]와 dp[i+1][j+1] 중에 더 큰 수가 현재 라인의 특정 값에 더해진다고 볼 수 있다.
- 따라서 최상층에는 최대값이 저장될 것 이다.
즉 밑에서부터 접근하는 경우 점화식은 다음과 같다.
dp[i][j] += Math.max(dp[i+1][j], dp[i+1][j+1]);다만 이때 맨 밑의 라인은 더해줄 필요가 없으므로 '맨 밑 라인 + 1 번째 라인'부터 해당 점화식을 적용한 반복문을 돌려주면 된다.
dp초기화는 주어진 triangle과 똑같이 선언하여 시작하면 된다. 이때 원본 데이터 보존을 위한 전략을 취해도 되고, 아니면 그냥 triangle 자체를 가지고 해당 점화식을 적용해도 문제 통과에는 지장이 없다. 여기서는 dp 배열에 triangle을 slice()로 복사해서 풀이했다. 사실 원본 배열이 2차원 배열이기에 얕은 복사(Shallow Copy)로 인해 Immutable에 대한 속성을 해치기에 사실 원본 데이터를 보전하기엔 의미가 없다...
코드
function solution(triangle) {
const dp = triangle.slice();
// (원본 배열 길이 - 2) 라인부터 0까지 진행하는 것에 주의하자
for(let i = dp.length-2; i >= 0; i--) {
for(let j = 0; j < dp[i].length; j++) {
dp[i][j] += Math.max(dp[i+1][j], dp[i+1][j+1]);
}
}
return dp[0][0];
}
