[프로그래머스] LV.3 모두 0으로 만들기 (JS)

문제

각 점에 가중치가 부여된 트리가 주어집니다. 당신은 다음 연산을 통하여, 이 트리의 모든 점들의 가중치를 0으로 만들고자 합니다.

• 임의의 연결된 두 점을 골라서 한쪽은 1 증가시키고, 다른 한쪽은 1 감소시킵니다.

하지만, 모든 트리가 위의 행동을 통하여 모든 점들의 가중치를 0으로 만들 수 있는 것은 아닙니다. 당신은 주어진 트리에 대해서 해당 사항이 가능한지 판별하고, 만약 가능하다면 최소한의 행동을 통하여 모든 점들의 가중치를 0으로 만들고자 합니다.

트리의 각 점의 가중치를 의미하는 1차원 정수 배열 a와 트리의 간선 정보를 의미하는 edges가 매개변수로 주어집니다. 주어진 행동을 통해 트리의 모든 점들의 가중치를 0으로 만드는 것이 불가능하다면 -1을, 가능하다면 최소 몇 번만에 가능한지를 찾아 return 하도록 solution 함수를 완성해주세요. (만약 처음부터 트리의 모든 정점의 가중치가 0이라면, 0을 return 해야 합니다.)

제한

• a의 길이는 2 이상 300,000 이하입니다.
  • a의 모든 수는 각각 -1,000,000 이상 1,000,000 이하입니다.
  • a[i]는 i번 정점의 가중치를 의미합니다.
• edges의 행의 개수는 (a의 길이 - 1)입니다.
  • edges의 각 행은 [u, v] 2개의 정수로 이루어져 있으며, 이는 u번 정점과 v번 정점이 간선으로 연결되어 있음을 의미합니다.
  • edges가 나타내는 그래프는 항상 트리로 주어집니다.

입출력 예시

a	edges	result
[-5,0,2,1,2]	[[0,1],[3,4],[2,3],[0,3]]	9
[0,1,0]	[[0,1],[1,2]]	-1

풀이

프로그래머스 월간 코드 챌린지 시즌2에서 출제된 따끈따끈한 문제다. 뭔가 그림까지 첨부되어 괜시리 복잡하게 보이지만 DFS 알고리즘을 이용하면 간단하게 풀이할 수 있다. 다만 문제는 우리의 JS로는 빙빙 돌아가서 풀이해야 한다는 점이다..!

앞서 포스팅한 여러 DFS 관련 알고리즘 문제에서도 간단하게 언급한 바 있는데, JS로는 DFS를 재귀적으로 풀기 여간 까다로운 것이 아니다. 브라우저에서도 (버전별로 다르겠지만) 재귀호출을 10만번 이상 깊게 들어가기 버거워하는데, 시간과 공간제약을 받는 알고리즘 문제 특성과 따로 Node.js를 통해 자바스크립트 구동 환경을 만든 프로그래머스의 ide 환경에서는 더더욱 재귀에 대한 제약이 심하다고 볼 수 있다.

제한 조건을 보면 a의 길이가 최대 30만인데, 만약 테스트 케이스 중에 30만 길이를 가진 배열이 등장하면 재귀 호출 스택이 터질 것은 너무나 자명하고 또 실제로도 런타임 에러가 등장한다. 때문에 우리는 JS로 DFS 문제를 풀때 재귀적으로 해결하는 것이 더 편할지라도 문제의 제약 조건으로 인해 울며 겨자 먹기로 다른 방식을 이용해 풀어야 할 경우가 많다. (역시 알고리즘은 C++이나 파이썬으로 갈아타도록 하자) 이와 관련된 조금 더 깊은 이야기는 여기에서 따로 포스팅 해두었으니 관심이 있으면 살펴보도록 하자.

다시 본론으로 돌아와서 먼저 재귀적으로 접근을 할 것이다. 재귀적인 풀이 방법을 먼저 구현하고 나서 그리고 해당 풀이를 Iterative DFS 방식으로 구현하고자 한다. 여기서 Iterative는 '반복적인' 이라는 뜻을 가지고 있다. 자바에서 Iterator를 다뤄본 분들은 눈치를 채셨겠지만 주로 배열, 자바의 ArrayList, JS Map ... 과 같이 반복적으로 셀 수 있는 (탐색이 가능한) 자료형과 연관이 있다고 보면 될 것 같다. 쉽게 말해 DFS 는 재귀함수로 구현하는 경우와 Stack을 이용해 구현하는 경우가 있는데 Iterative DFS 는 Stack을 이용해 구현한다고 보면 되겠다.

그래프 생성

먼저 문제에서 주어지는 edges는 항상 트리 형태로 주어진다고 명시되어 있다. 즉 우리는 사이클이 없는 그래프를 입력으로 받는다고 생각할 수 있다. 이때 간선의 정보는 정렬되어 있지는 않기 때문에, 간선 정보를 가지고 그래프(또는 트리) 형태로 만들어주는 과정이 필요하다. 이는 그래프 탐색 문제에서 항상 공통되는 과정이고 앞서 그래프 관련 포스팅에서도 여러번 살펴보았으니 바로 코드로 구현하자.

// 여기서 a는 각 노드의 값을 담고 있는 배열이다.
// 즉 노드 개수만큼의 배열을 만들고 이를 그래프 형태로 활용할 것이다.
const tree = new Array(a.length).fill().map(_ => []);
// 간선의 정보를 통해 양방향 그래프 (또는 트리) 형태로 생성
// 여기서는 간선의 번호가 0번 부터 시작하므로
// 배열 index와 값이 일치하기 때문에 아래와 같이
// 별도의 값 조정 없이 바로 트리를 만들어 줄 수 있다.
// 만약 1번부터 시작하는 간선 정보를 받았다면
// [u-1]  ... push(v-1) 등의 작업이 필요할 수 있다.
for(const [u, v] of edges) {
  tree[u].push(v);
  tree[v].push(u);
}

그러면 이제 문제에 조건에 맞게 어떻게 접근해야 할지 살펴보자. 이미 DFS에 대해 실컷 이야기 했으니 DFS로 접근해야 한다는 걸 알겠지만 잠시 잊어버리고 처음부터 접근해보자.

모두 0으로 만들 수 있는 조건

먼저 트리의 각 노드의 가중치를 모두 0으로 만들 수 있는 방법에 대해 생각해보자. 이는 비교적 간단하게 떠올릴 수 있다. 노드의 가중치를 모두 0으로 만들기 위해서는 최소 연결된 두 개의 노드의 합이 0이 되어야 한다.예를 들어 A노드의 값은 2이고, B노드의 값은 -2일 때 이 두 개의 노드는 모두 0으로 만들 수 있다. A 또는 B에서 +2 / -2를 해주면 되기 때문이다.

그런데 세 개의 노드가 있을 때는 어떻게 판별할 수 있을까? 각 노드의 가중치를 더하거나 빼주는 작업은 오직 연결되어 있는 노드와 수행하는 것이다. 따라서 세 개의 노드의 합이 모두 0이 된다면, 모든 노드가 가중치 0을 만들 수 있다. 즉 우리는 다음과 같은 규칙 하나를 발견할 수 있다.

• 모든 노드 가중치의 합이 0이라면 모든 노드의 가중치를 0으로 만들 수 있다.

따라서 위 조건에 해당되지 않는 놈들은 모두 -1을 리턴하도록 하면 되겠다.

필요한 최소 행동 횟수 계산

그렇다면 0으로 만들 수 있는 그래프인지 아닌지는 판별했는데, 0으로 만들기 위한 최소 행동 횟수는 어떻게 얻을 수 있을까? 다시 앞으로 돌아가서 가중치에 영향을 줄 수 있는 노드는 오직 인접한 노드 뿐이라는 것을 떠올려보자. 그리고 다음 그림을 살펴보자.

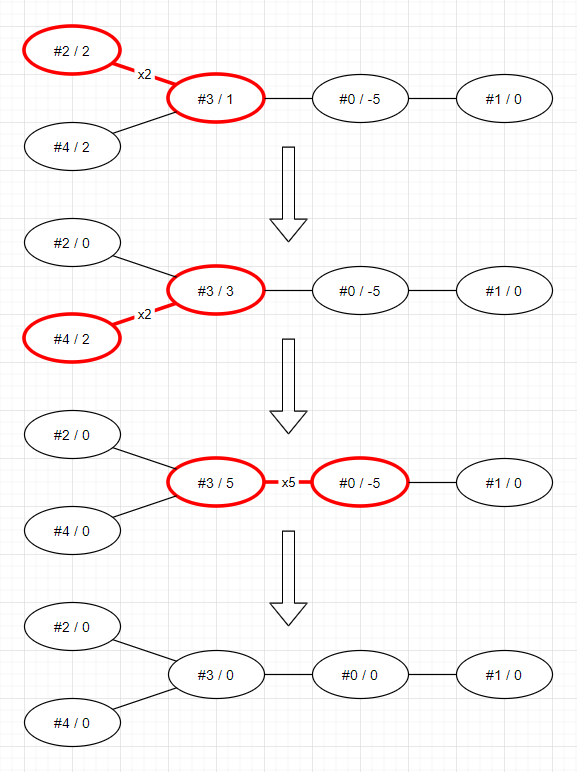
#3번 노드를 기준으로 연결되어 있는 노드는 #0, #2, #4번으로 총 3개이다. 따라서 #3번 노드의 가중치에 영향을 줄 수 있는 노드 역시 인접한 3개의 노드가 된다. 이때 #2번과 #4번 노드의 값을 먼저 0으로 만들고 다시 #3번 노드로 돌아와서 0으로 만들어주기 위해 감산한 값을 적용하는 것을 확인할 수 있다. 이 같은 흐름은 DFS 방식과 상당히 닮아있다.

#0번 노드가 DFS 탐색의 출발 노드라고 가정한다면, 0 -> 3 으로 내려간 뒤, 3번을 기점으로 2번과 4번을 먼저 탐색하게 될 것이다. 그리고 그 값을 다시 부모 노드였던 3번이 받게 된다. 즉 DFS 과정과 완전히 동일하다.

그렇다면 왜 DFS 탐색을 통해 최소 행동 횟수를 계산할 수 있는 것일까? 최소 행동 횟수를 계산하기 위해서는 최소한의 움직임이 발생해야 할 것이다. 위 그림에서 보여준 예시 역시 모든 노드의 합이 0이기 때문에 각 노드를 0으로 만들 수 있다. 즉 DFS 탐색을 하지 않더라도 어느 순간에는 모든 노드를 0으로 만들 수 있겠지만, 이는 최소 행동 횟수임을 보장할 수 없다. DFS는 리프노드 먼저 찾고, 다시 부모 노드로 돌아오면서 최종적으로 루트노드까지 돌아오는 구조가 되기 때문에 리프노드에서 연산해준 값을 계속 부모노드로 올릴 수 있다. 이 경우 인접한 노드끼리 각각 1번씩의 연산만 발생하기 때문에 최소 행동 횟수임을 보장할 수 있는 것이다.

이해가 잘 가지 않는다면 그림으로 보면 쉽다. 위의 그림을 기준으로 설명하자면 DFS 방식대로 진행할 시 9번의 행동을 통해 모든 노드를 0으로 만들 수 있는 것을 알 수 있다.

이때 리프노드에서 부터 접근하는 것이 아니라 #3번 노드의 값을 #2번 노드로 내려준다고 생각해보자. 그러면 #2번 노드의 값은 3이 될 것이고 #3번은 0이 될 것이다. 그렇지만 인접한 노드끼리 연산이 가능하기 때문에 결국 #2번 노드에 담긴 값을 다시 #3번으로 옮기는 불필요한 과정이 요구된다. 따라서 최소 행동 횟수를 보장할 수 없는 것이다.

위 과정을 간단하게 DFS 재귀호출 방식으로 구현하면 다음과 같다. 어차피 이 방식으로는 문제를 통과할 수 없기 때문에 visited와 같은 배열 선언 없이 최소한의 코드로 구현해보았다.

const dfs = (start, prev) => {
  // 현재 start와 연결된 노드들을 탐색할 것이다.
  for(const next of tree[start]) {
    // next와 prev가 같다는 것은 이미 방문했다는 뜻이다.
    if(next === prev) continue;
    // 방문을 하지 않았다면 next 노드를 탐색
    // 이때 부모는 당연히 start 노드가 된다
    dfs(next, start);
  }
  
  /* --- 리프노드 영역 --- */
}

// 출발 노드는 0번으로 하고
// 0번 노드는 루트노드이므로 부모가 없기 때문에 -1 지정
dfs(0, -1);

반복문 외부의 영역에 주석으로 '리프노드 영역' 이라고 썼는데, 엄밀히 말하면 더 이상 DFS 탐색으로 내려갈 노드가 없을 때 어떤 계산이 수행되는 부분이다. 추후 Iterative DFS를 구현할 때 쉽게 구분하기 위해 그냥 '리프노드 영역' 이라고 기술했다.

앞서서 리프노드부터 연산이 이루어져야 한다는 것을 증명했으므로 우리는 저 주석 처리된 부분에 로직을 구성해야 한다. 그림에서 보면 알겠지만 행동 횟수는 현재 노드가 가지고 있는 값과 절대값이 동일하다. 즉 횟수이기 때문에 플러스를 하든 마이너스를 하든 노드의 가중치가 곧 횟수가 되는 것이다. 따라서 행동 횟수는 절대값의 연산이 필요할 것이다.

그러나 리프노드에서 부모노드로 옮겨가는 값은 노드의 가중치 본연의 값이다. 즉 음수면 마이너스, 양수면 플러스가 부모노드에게 작용한다. 따라서 다음의 두 로직이 필요하다.

1. sum += Math.abs(a[start]);

   • a[start]는 항상 주석 영역에서 더 이상 내려갈 곳이 없는 현재 노드의 영역이다. 이 가중치를 절대값으로 횟수에 더해준다.

2. a[prev] += a[start];

   • a[prev]는 현재 노드의 부모노드를 말한다. 현재 노드의 가중치를 부모 노드에게 합산해야 한다.

이를 모두 적용하여 DFS 함수를 구현하면 다음과 같다.

let sum = 0;
const dfs = (start, prev) => {
  for(const next of tree[start]) {
    if(next === prev) continue;
    dfs(next, start);
  }
  
  sum += Math.abs(a[start]);
  a[prev] += a[start];
}

dfs(0, -1);

그리고 문제에서 원하는 값은 a[0]을 기준으로 갈리게 될 것이다. DFS 탐색을 0번 노드부터 했기 때문에 a[0]은 루트노드가 될 것이고, 만약 모든 노드를 0으로 만들 수 있다면 우리가 앞서 찾은 조건에 의해 a[0]의 값이 0이 되어있을 것이다. 따라서 이 값이 0이면 위에서 계산한 sum을 리턴하고 그렇지 않으면 -1 을 리턴하도록 한다.

// a[0]이 참이면 모든 노드를 0으로 만들 수 없다는 것이다.
return a[0] ? -1 : sum;

그런데...?

위 과정의 코드를 모두 복사하여 실행해보면 테스트를 잘 통과하는 것을 확인할 수 있다. 그러나! 앞서 줄곧 밑밥을 깔아논 덕에 해보지 않아도 알 수 있겠지만 혹여나 하고 제출을 해보면 특정 케이스는 런타임 에러가 뜨는 것을 볼 수 있다..

이는 주어진 배열 값이 너무 커서 자바스크립트의 호출 스택이 재귀 함수의 누적을 버티지 못하고 터져버린 경우이다. (자바스크립트의 호출스택은 넘나 연약하다..) 때문에 자바스크립트로 이 문제를 통과하기 위해서는 재귀호출 DFS 방식대신 Stack을 이용한 Iterative DFS 를 구현해야 한다. 물론 파이썬이나 C++의 경우 똑같은 로직으로 정상 통과하는 것을 확인했다. (파이썬은 대신 recusionlimit을 풀어주어야 한다)

Migration to Itreative DFS

자 위에서 우리가 구현했던 DFS를 Stack을 활용하는 버전으로 마이그레이션 해보자. Iterative DFS 관련해서는 앞에서 언급한 여기 포스팅에 조금더 상세히 기술되어 있다.

먼저 stack과 방문 여부를 체크할 수 있는 visit 배열을 만들어두자. 그리고 시작 노드는 0부터 탐색할것이기 때문에 stack을 선언과 동시에 0번 노드로 초기화 해준다. 이때 우리는 부모노드가 누구인지 판단할 정보가 필요하다. 위에서 구현한 DFS 에서는 prev 매개변수로 이 값을 전달했지만 stack을 이용해서는 이를 따로 전달하기 보단, 현재 노드에게 부모 노드 정보를 바로 연결하도록 구성하자. 즉 다음과 같이 초기화가 가능하다.

// 0은 시작노드, -1은 부모노드이다.
// 위에서와 동일하게 0이 루트이므로 이 경우 부모노드는 -1이다.
const stack = [ [0, -1] ];
// 첫 방문 여부는 모두 false로 초기화한다.
const visit = new Array(a.length).fill(false);

이젠 stack이 빌 때 까지 반복문을 돌면서 pop을 해줄 것이다. stack의 LIFO 원칙에 의해 pop을 하게 되면 가장 마지막에 들어간 원소가 나오게 된다. 우리는 노드 하나를 stack에서 pop을 하고나서 방문 여부를 체크해준 뒤 다시 stack에 해당 노드를 넣어줄 것이다. 이를 통해 위에서 구현한 재귀방식의 DFS 처럼, 더 이상 내려갈 곳이 없는 노드에서의 연산 공간을 만들어 줄 수 있다. 이 역시 이해가 가지 않는다면 포스팅을 참고하자. 즉 다음이 구현할 수 있다.

let sum = 0;
while(stack.length) {
  const [start, parent] = stack.pop();
  
  // 이미 방문했던 노드를 다시 만나는 시점이 결국
  // 더 이상 내려갈 곳이 없는 노드를 마주한 경우이다.
  if(visit[start]) {
    /* --- 리프노드 영역 --- */
    continue;
  }
  
  // 위 조건에 걸리지 않는다면 현재 start 노드는
  // 처음 방문하는 노드가 된다.
  // 따라서 해당 노드를 다시 stack에 넣어주고
  // 방문여부를 true 로 변경한다.
  stack.push([start, parent]);
  visit[start] = true;
  
  // 위 DFS 함수에서 자신을 호출하는 영역과 유사하다.
  // 대신 별도의 visit 배열을 통해 방문여부를 체크한다.
  for(const next of tree[start]) {
    if(!visit[next]) {
      stack.push([next, start]);
    }
  }
}

위에서 DFS 함수를 구현할 때도 주석처리로 '리프노드 영역' 이라고 기술했다. (엄연히 리프노드만을 위한 영역은 아님!) 동일하게 위에서도 해당 영역이 '리프노드 영역'이 되겠다. 따라서 우리가 위에서 해준 연산을 저 영역에 그대로 구현하면 된다. 즉 다음과 같이 구현하자.

// continue가 추가된 점 외에는
// 위에서 구현한 DFS 내부 로직과 동일하다.
if(visit[start]) {
  sum += Math.abs(a[start]);
  a[parent] += a[start];
  continue;
}

아니 또 왜!?

이제 앞서 구현한 DFS 함수는 지우고 위의 반복문으로 대체하면 정상적으로 테스트를 통과하는 것을 확인할 수 있다. 아! 그런데 제출하니 8번만 통과를 하지 못하고 있다. 따로 런타임에러가 아닌 실패가 뜨는 것을 보아하니 호출 스택이 터지거나 로직의 문제로 인한 무한루프는 아닌듯하다. 이것 때문에 삽질을 좀 했는데 결론부터 말하자면 최소 행동 횟수의 값이 정수범위를 넘어가는 경우가 생기는 것 같다. 배열의 최대 길이가 30만이고 노드 가중치의 최대값이 100만이기 때문에 이 범위를 벗어난 값이 제대로 계산되지 않아 계속 실패가 뜬것 같다. 따라서 행동 횟수를 저장하는 변수 sum 을 BigInt 자료형을 활용하여 다음과 같이 계산하면 정상적으로 통과할 수 있다.

// 정수 뒤에 n을 붙이면 BigInt 자료형으로 인식한다.
let sum = 0n;

...

// sum이 BigInt 형이므로 절대값 역시
// 동일한 자료형으로 계산해주자.
sum += BigInt(Math.abs(a[start]));

...

전체코드

주석을 제외한 전체코드는 다음과 같다. 무난한 난이도의 문제였지만 JS로 DFS를 구현하는데 삽질 + BigInt 문제를 찾아내느라 삽질...로 인해 삽질 가득한 문제였다.

function solution(a, edges) {
  const tree = new Array(a.length).fill().map(_ => []);
  for(const [u, v] of edges) {
    tree[u].push(v);
    tree[v].push(u);
  }
  
  const stack = [ [0,-1] ];
  const visit = new Array(a.length).fill(false);
  
  let answer = 0n;
  while(stack.length) {
    const [start, parent] = stack.pop();
    
    if(visit[start]) {
      a[parent] += a[start];
      answer += BigInt(Math.abs(a[start]));
      continue;
    }
    
    stack.push([start, parent]);
    visit[start] = true;
    
    for(const next of tree[start]) {
      if(!visit[next]) {
        stack.push([next, start]);
      }
    }
  }
  
  return a[0] ? -1 : answer;
}

출처

https://programmers.co.kr/learn/courses/30/lessons/76503?language=javascript