[프로그래머스] LV.3 합승 택시 요금 (JS)

KG·2021년 4월 23일
DPLv.3그래프알고리즘카카오프로그래머스플로이드-와샬
2

알고리즘

목록 보기
32/61
post-thumbnail

문제

밤늦게 귀가할 때 안전을 위해 항상 택시를 이용하던 무지는 최근 야근이 잦아져 택시를 더 많이 이용하게 되어 택시비를 아낄 수 있는 방법을 고민하고 있습니다. "무지"는 자신이 택시를 이용할 때 동료인 어피치 역시 자신과 비슷한 방향으로 가는 택시를 종종 이용하는 것을 알게 되었습니다. "무지"는 "어피치"와 귀가 방향이 비슷하여 택시 합승을 적절히 이용하면 택시요금을 얼마나 아낄 수 있을 지 계산해 보고 "어피치"에게 합승을 제안해 보려고 합니다.

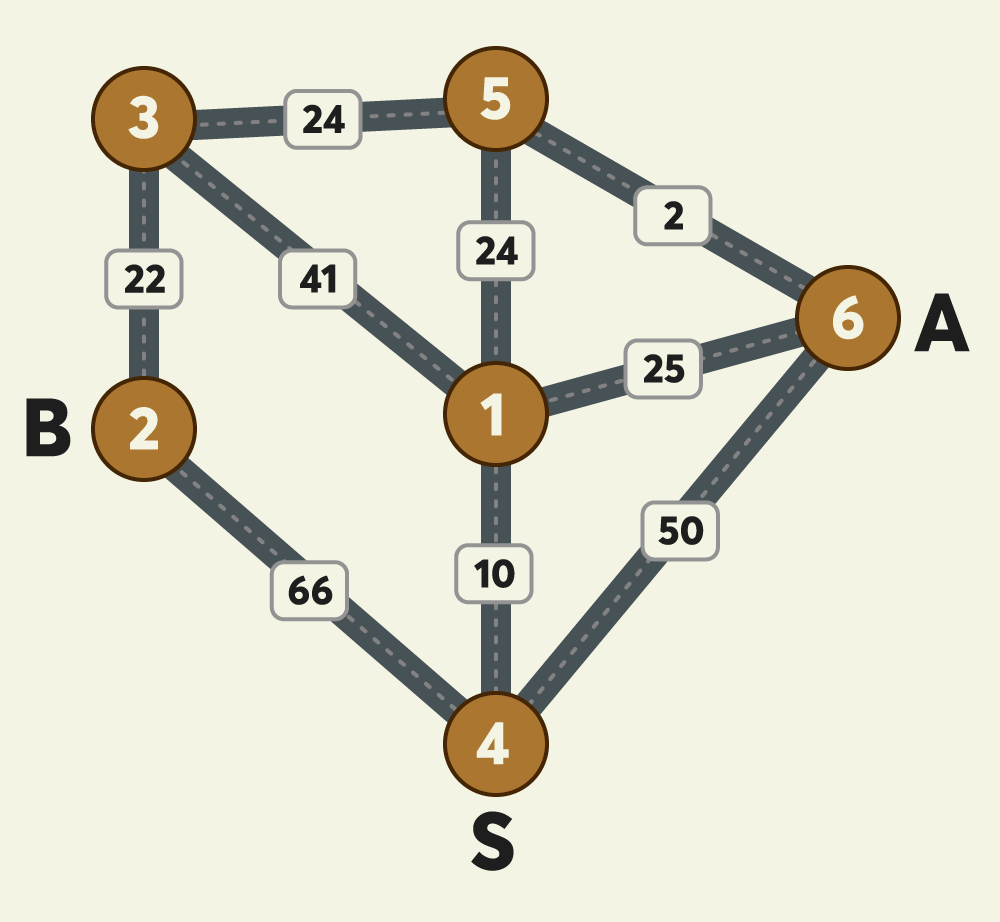
위 예시 그림은 택시가 이동 가능한 반경에 있는 6개 지점 사이의 이동 가능한 택시노선과 예상요금을 보여주고 있습니다.
그림에서 A와 B 두 사람은 출발지점인 4번 지점에서 출발해서 택시를 타고 귀가하려고 합니다. A의 집은 6번 지점에 있으며 B의 집은 2번 지점에 있고 두 사람이 모두 귀가하는 데 소요되는 예상 최저 택시요금이 얼마인 지 계산하려고 합니다.

지점의 개수 n, 출발지점을 나타내는 s, A의 도착지점을 나타내는 a, B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성해 주세요.
만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 더 낮다면, 합승을 하지 않아도 됩니다.

제한

  • 지점갯수 n은 3 이상 200 이하인 자연수입니다.

  • 지점 s, a, b는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.

    • 즉, 출발지점, A의 도착지점, B의 도착지점은 서로 겹치지 않습니다.

  • fares는 2차원 정수 배열입니다.

  • fares 배열의 크기는 2 이상 n x (n-1) / 2 이하입니다.

    • 예를들어, n = 6이라면 fares 배열의 크기는 2 이상 15 이하입니다. (6 x 5 / 2 = 15)
    • fares 배열의 각 행은 [c, d, f] 형태입니다.
    • c지점과 d지점 사이의 예상 택시요금이 f원이라는 뜻입니다.
    • 지점 c, d는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
    • 요금 f는 1 이상 100,000 이하인 자연수입니다.
    • fares 배열에 두 지점 간 예상 택시요금은 1개만 주어집니다. 즉, [c, d, f]가 있다면 [d, c, f]는 주어지지 않습니다.

  • 출발지점 s에서 도착지점 a와 b로 가는 경로가 존재하는 경우만 입력으로 주어집니다.


입출력 예시

nsabfaresresult
6462[[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]]82
7341[[5, 7, 9], [4, 6, 4], [3, 6, 1], [3, 2, 3], [2, 1, 6]]14
6456[[2,6,6], [6,3,7], [4,6,7], [6,5,11], [2,5,12], [5,3,20], [2,4,8], [4,3,9]]18

풀이

2021 카카오 블라인드 테스트에서 출제된 문제이다. 뭔가 그래프와 관련된 이미지가 나오고, 게다가 지문까지 기니깐 괜시리 포기하고 싶은 마음을 들게한다. 그렇지만 해당 문제는 그렇게 어려운 문제가 아니다(?). 이전 포스트에서 '플로이드-와샬' 알고리즘을 이용하여 문제를 풀면서 관련 알고리즘에 대한 설명을 간략하게 했는데 해당 문제 역시 플로이드-와샬 알고리즘을 이용해 풀 수 있다. 만약 플로이드-와샬 알고리즘이 어떤 알고리즘인지 정확하게 모른다면 위 포스트 글을 먼저 참고해서 읽어보자.

그래프 연결리스트

항상 그래프 관련 문제를 풀때 필요한 사전작업이다. 그래프의 노드가 연결된 형태의 배열을 미리 제공해 주는 경우도 있지만 대부분의 경우는 정렬되지 않은 상태의 노드 간 연결 정보만 던져 준다. 해당 문제에서는 fares 배열에 각 노드간 연결 정보와 간선의 가중치가 담겨 있으므로 이를 활용해서 그래프 연결리스트를 만들어주자. 이때 시작 노드가 1번부터 번호가 할당되고 있으므로, 그래프 배열에 저장할 때 노드번호 - 1 index에 저장하던가 0번 index를 비워서 사용하는 방법이 있을 것이다. 여기서는 전자의 방법으로 그래프 연결리스트를 생성해주자. 또 가중치에 대한 정보를 배열로 매핑해서 넣어주자.

const graph = new Array(n).fill().map(_ => []);
fares.forEach(pos => {
  const [x, y, weight] = pos;
  graph[x-1].push([y-1, weight]);
  graph[y-1].push([x-1, weight]);
}

플로이드-와샬 알고리즘

뭔가 이미지도 있고, 설명도 길어서 굉장히 복잡해보이지만 결국 문제가 원하는 답은 최소 요금이 나오는 경로이다. 이때 요금은 각 노드끼리 연결된 간선에 가중치로 부여되어 있다. 즉 최소 요금을 구하기 위해서는 우리가 기존에 사용하는 최단 경로 알고리즘을 활용하면 최소 요금을 쉽게 구할 수 있을 것 같다는 생각이 든다. 요금으로 주어진 가중치를 거리 정보로 생각하여 접근하면 되기 때문이다.

최단 경로를 구하기 위해 다양한 알고리즘이 있지만 앞서 언급한 바와 같이 '플로이드-와샬' 알고리즘을 사용하여 문제를 풀도록 하자. 왜냐하면 우리가 해당 문제를 풀기 위해서는 모든 정점에서 각각의 정점으로 향하는 최단 경로, 즉 최소 요금을 사용하는 경로를 파악해야 하기 때문이다. 이에 적합한 알고리즘으로 가장 대표적인게 플로이드-와샬 알고리즘이다.

그렇다면 왜 모든 정점에서 각각의 정점으로 향하는 최단 경로가 필요한 것일까? 문제에서 우리는 출발점 s에서 시작하여 각각 a와 b 로 향하는 두사람이 있다. 두 사람은 최소 요금을 위해 합승을 할 수도 있고, 각자 따로 가는 것이 더 저렴하다면 합승없이 따로 각자의 목적지까지 갈 수도 있다. 즉 시작노드에서 각자의 목적지까지 이동하는 최소 요금은 합승을 어디까지 하느냐에 따라 결정된다. 이때 마지막 합승 지점 역시 그래프 상의 한 노드이며, 해당 노드에서 두 사람은 각각 따로 자신의 목적지를 향하게 될 것이다. 따라서 합승 지점은 주어진 n개의 노드를 하나씩 돌면서, 각 합승지점에서 각자의 목적지로 향하는 최단 경로를 다시 탐색하기 때문에 우리는 각각의 노드에서 모든 노드로 향하는 최단 경로가 필요한 것이다.

플로이드-와샬 알고리즘 구현

플로이드 와샬 알고리즘을 쓰기로 했다면, 우리가 처음에 사용한 그래프 정보를 다시 작성해주어야 한다. 플로이드-와샬 알고리즘은 DP로 접근하여 각 노드로부터 모든 정점에 대한 최단 경로를 구하기 때문이다. 즉 board 라는 DP배열을 하나 만들어두었다면 다음의 의미를 갖는다. (이에 대한 자세한 풀이는 위에 언급한 포스트에서 참고할 수 있다.)

  • board[i][j] : i노드에서 j노드까지 최단 경로

따라서 다음과 같이 플로이드-와샬 알고리즘을 적용할 DP 배열로 그래프 정보를 바꾸어주자.

// n개 노드에 대해 모든 정점(n개)으로 향하는 DP배열
// 초기값은 Infinity(최단경로없음)으로 설정
const board = new Array(n).fill().map(_ => new Array(n).fill(Infinity));

// 자기 자신에 대한 최단 경로는 0으로 설정
for(let i = 0; i < n; i++) {
  board[i][i] = 0;
}

// 주어진 연결 정보로 DP 배열 초기화
fares.forEach(pos => {
  const [x, y, weight] = pos;
  // x에서 y로 향하는 최단경로(최소요금) = weight
  board[x-1][y-1] = weight;
  board[y-1][x-1] = weight;
});

DP 배열의 초기화를 마쳤다면 경유노드 k를 통해 플로이드-와샬 알고리즘을 구현하자. 다음과 같이 3중 반복문을 통해 구현할 수 있다.

// k는 경유노드, i는 시작노드, j는 도착노드
for(let k = 0; k < n; k++) {
  for(let i = 0; i < n; i++) {
    for(let j = 0; j < n; j++) {
      if(board[i][k] + board[k][j] < board[i][j])
        board[i][j] = board[i][k] + board[k][j];
    }
  }
}

최소 요금 경로

플로이드-와샬 알고리즘을 통해 각 정점에서 모든 정점에 대한 최단 경로를 구해주었다. 그렇다면 이제 두 사람이 각각의 목적지로 향할 때의 최소 요금 경로를 구해주도록 하자.

방법은 왜 플로이드-와샬 알고리즘을 적용할 것인지 설명하면서 이미 언급했는데, 우리는 주어진 n개의 노드를 모드 두 사람의 합승 도착 지점으로 설정할 것이다. 그리고 두 사람은 해당 합승 지점에서 각자의 목적지로 향하게 될 것이고, 이때의 합을 모두 더해준다면 n개에 대한 최소 요금 경로가 모두 나올 것이다. 여기서 가장 최소값을 리턴해주면 정답이 될 것이다. 즉 s가 출발점이고, 반복문에서 i가 합승지점, 그리고 a와 b는 각각 두 사람의 목적지라고 할 때, 다음과 같은 식이 성립한다.

// 시작점에서 합승지점까지 + 합승지점에서 a까지 + 합승지점에서 b까지
const shortest = board[s-1][i] + board[i][a-1] + board[i][b-1];

이때 두 사람이 각각 따로 가는 경우도 최소 요금이 될 수 있기 때문에 이를 고려해주어야 한다. 따라서 default answer 값을 따로 가는 경로로 계산을 해주고 최소값을 갱신해주자.

// 기본 answer = 두 사람이 따로 가는 경우
let answer = board[s-1][a-1] + board[s-1][b-1];

for(let i = 0; i < n; i++) {
  const shortest = board[s-1][i] + board[i][a-1] + board[i][b-1];
  // 기존값과 새로 계산된 값 중 더 작은 값으로 갱신
  answer = Math.min(answer, shortest);
}

return answer;

전체코드

주석을 제외한 전체 코드는 다음과 같다.

function solution (n, s, a, b, fares) {
  const board = new Array(n).fill().map(_ => new Array(n).fill(Infinity));
  
  for(let i = 0; i < n; i++) 
    board[i][i] = 0;
  
  fares.forEach(pos => {
    const [x, y, weight] = pos;
    board[x-1][y-1] = weight;
    board[y-1][x-1] = weight;
  });
  
  for(let k = 0; k < n; k++) {
    for(let i = 0; i < n; i++) {
      for(let j = 0; j < n; j++) {
        if(board[i][j] > board[i][k] + board[k][j])
          board[i][j] = board[i][k] + board[k][j];
      }
    }
  }
  
  let answer = board[s-1][a-1] + board[s-1][b-1];
  for(let i = 0; i < n; i++) {
    const shortest = board[s-1][i] + board[i][a-1] + board[i][b-1];
    answer = Math.min(answer, shortest);
  }
  
  return answer;
}

출처

https://programmers.co.kr/learn/courses/30/lessons/72413

profile
KG
개발잘하고싶다
이전 포스트

[프로그래머스] LV.3 자물쇠와 열쇠 (JS)

다음 포스트

[프로그래머스] LV.3 광고 삽입 (JS)

0개의 댓글