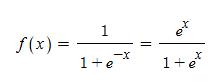[빅데이터분석기사] Part2 - CH 02. 데이터 탐색

Chapter 02. 데이터 탐색

---

Section 01. 데이터 탐색의 기초

1. 탐색적 데이터 분석 : EDA

• 수집한 데이터에 대해 다양한 방법으로 관찰 / 이해하는 과정

필요성

• 내재된 잠재적 문제에 대한 이해 및 해결안 도출
• 문제 정의 단계에서 놓친 새로운 양상 / 패턴 발견

분석 과정 및 절차

1. 분석 목적, 변수 확인
2. 데이터 문제성(결측치 유무, 이상치 유무) 확인
3. 데이터 개별 속성값이 예상 범위 분포 내에 위치하는지 확인
4. 데이터 간 상관관계 확인 -> 상관분석

이상치 검출방법

1. 개별 데이터 관찰
2. 통계값 활용
   • IQR : 사분위 범위 기반 이상치 제거
   • 정규분포 : μ - 2σ ~ μ + 2σ
3. 시각화
4. 머신러닝 ( ex) K-means)

---

2. 상관관계 분석

• 두 변수간 선형적 관계 분석

  두 변수는 독립적이거나 상관 관계에 있다.

상관분석

• 단순 상관분석
  : 2개 변수 간 관계의 강도

• 다중 상관분석
  : 3개 이상 변수 간 관계의 강도

  • 편 상관관계분석 (Partial)
    : 다른 변수와의 관계는 고정, 두 변수 간 관계 강도만 측정

상관분석의 기본 가정

1. 선형성
   : X, Y간 관계가 직선적인가?
   : 산점도를 통해 확인

2. 동변량성(등분산성)
   : X 값에 관계 없이 Y 값의 흩어짐 정도가 일정한가

3. 두 변인의 정규분포성
   : X, Y의 측정치 분포가 모집단에서 정규분포를 따르는가

4. 무선독립표본
   : 모집단에서 추출된 모든 표본이 서로 독립적
   : 한 관측치의 값이 다른 관측치의 값에 영향 X

상관분석 방법

• 두 변수 간 관계를 측정하는 통계량으로 판단

1. 피어슨 상관계수 : Pearson Correlation Coefficient

• 두 변수 간의 선형 관계(linear)의 강도 / 방향 측정
  • 한 변수가 증가할 때, 다른 변수가 증가 or 감소
• X, Y간 선형 상관 관계를 -1 ~ 1 값으로 측정
  : +1 = 양의 상관
  : 0 = 상관 관계 X
  : -1 = 음의 상관
• Outlier에 민감함
• 데이터가 정규분포, 등분산성을 만족해야 함

  키 - 몸무게, 공부 시간 - 성적 등

2. 스피어만 상관계수 : Spearman Correlation Coefficient

• 두 변수 간의 단조 관계(monotonic)의 강도 / 방향 측정
  • 한 변수가 증가할 때, 다른 변수도 항상 증가 or 항상 감소
  • 반드시 직선적일 필요는 없음
• 실제 데이터 값 대신 순위(rank)를 통해 계산
• 두 변수의 차이 ∝ 스피어만 상관 계수 값
  • 1에 가깝다. = 단조적 상관석
  • 0 = 상관성이 없다.
• Outlier 영향 적음
• 데이터 분포에 대한 가정 불필요

  고객 만족도 순위 - 제품 품질 순위 등

---

3. 기초통계량 추출 및 이해

1. 중심화 경향 기초통계량

• 산술 평균
  : 모평균μ, 표본 평균X (X_bar)

• 기하 평균
  : n개의 양수들을 모두 곱한 후 n제곱근을 취한 값
  

: 평균물가상승률 의 비율, 성장률 값에 대한 평균
: 일반적으로 산술 평균 ≥ 기하 평균

• 조화 평균
  : 각 요소의 역수에 대한 산술 평균 → 역수
  : 자료 동일 시, 조화 = 산술 = 기하
  : 자료 상이 시, 조화 ≤ 기하 ≤ 산술

• 중앙값

• 최빈값

• 분위수
  : 자료의 위치
  : 몇등분 하느냐에 따라 사분위수, 십분위수 등

2. 산포도 = 분산도

: 자료의 퍼짐 정도
: 중심 위치의 측도 + 중심 경향도 수치에서 자료의 떨어짐 정도

• 분산, 표준편차
  : 평균을 중심으로 밀집/퍼짐의 정도
  : 각 자료값에 대한 정보 반영
  : 특이점에 영향이 크다.
  : 분산 ∝ 자료의 분포형태

• 범위
  : MAX ~ MIN

• 평균 절대편차 : MAD
  : | 자료값과 표준평균과의 편차 |에 대한 산술평균
  : ∑|X - AVG| / n

• 사분위 범위 : IQR
  : Q3 - Q1, 이상치 판단에 사용

• 변동계수 : CV
  : 평균을 중심으로 한 산포의 상대적 척도
  : CV ∝ 분포의 정도

3. 자료의 분포 형태

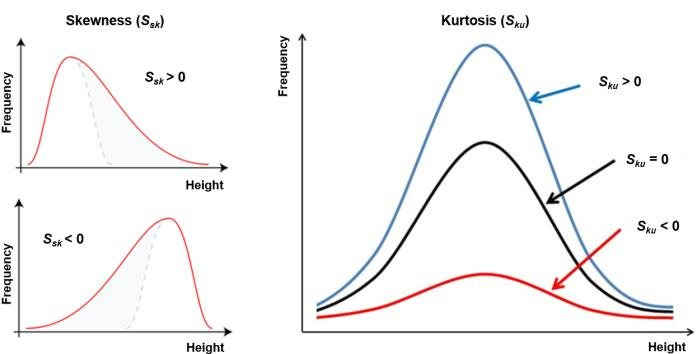
• 왜도 : Skewness
  : 분포의 비대칭 정도, 대칭성/비대칭성 정량화
  : 왜도 = 0 → 대칭, 평균 = 중앙값 = 최빈값
  : 왜도 > 0 → 왼쪽 치우침, 평균 > 중앙값 > 최빈값
  : 왜도 < 0 → 오른쪽 치우침, 평균 < 중앙값 < 최빈값
  : 분포의 비대칭성 및 크기를 통해 이상치 존재 파악
  • |왜도| > 1.96 → 비대칭성

피어슨 비대칭 계수
: 분포가 좌우로 얼마나 대칭적인지
: 왜도를 측정하는 간단한 통계량

1. 최빈값을 알 때 : 제 1 비대칭 계수
   
2. 최빈값 모를 때 : 제 2 비대칭 계수
   

• 첨도 : Kurtosis
  : 분포의 뾰족한 정도
  : 평균에 몰릴 수록 첨도가 높음
  : 첨도 > 3 → 뾰족, 첨도 = 3 → 정규 분포, 첨도 < 3 → 평평

---

4. 시각적 데이터 탐색

1. 통계적 시각화

• 도수 분포표
  : 계급에 의한 분류
  : 질적자료를 범주에 대한 도수(상대도수)로 표현

  • 상대도수 : 도수 / n

• 히스토그램
  : 도수분포표를 통해 표분의 자료분포 표현
  : 가로축 = 수량

• 막대 그래프, Pie Chart

• 산점도 : Scatter Plot

• 줄기 잎 그림

• 상자 수염 그림 : Box Plot

---

Section 02. 고급 데이터 탐색

1. 시공간 데이터 탐색

다차원 데이터 : 공간 정보 + 시간적 흐름

• 시간 데이터
  : 어느 한 시점에 대한 스냅샷 정보
  : 유효시간, 거래시간, 이원시간(거래 + 유효) 등

• 공간 데이터
  : 레스터 공간(실세계 객체 이미지), 벡터 공간, 기하학적 타입, 위상(공간 객체 간 관계)

  공간 데이터 모델

  1. 관계형
     : 데이터 표현 유연하지 않음
     : 실세계 객체 표현 X

  2. 객체지향
     : 비구조적, 데이터 표현 자연스러움
     : 연산 및 확장, 무결성 검사 쉬움

시공간 데이터 분석

• 시공간위상 관계 연산
  1. 공간위상 연산자
     : 두 객체 간 공간 영역 상 관계에 대한 True/False
  2. 시간 관계
     : 두 객체 간 선후 관계에 대한 True/False

• 시공간 기하 연산
  1. 공간 기하
     : 두 객체 간의 거리
  2. 시간 구성
     : 객체의 유효기간 변경

---

2. 다변량 데이터 탐색

: 변수 간 인과관계 규명 및 분석

종속변수와 독립변수 간 인과관계 탐색법

1. 다중 회귀 : Multiple Regression

• 독립변수 2개 이상의 회귀 모형
  • 각 독립변수는 종속변수와 선형 관계
• 종속변수 Y에 대해 독립변수 X가 k개
• 회귀 모형은 모수에 대해 선형
• 오차항의 평균 = 0, 오차항은 정규분포 추종
  • 오차항 : 관측치와 모예측치 간 편차 차이
• 최소자승법 사용

2. 로지스틱 회귀 : Logistic Regression

• 독립변수의 선형 결합을 통해 사건의 발생 가능성 예측
• 이항형 데이터(변수 2개) → 종속변수 Y = [0, 1]
• 이진적 종속변수에 대해 P(y|x)는 이항분포
• 독립변수는 형태 상관 없음
  • 종속변수는 연속 or 이산
    

3. 분산 분석 : ANOVA

• 2개 이상 집단 평균이 통계적으로 유의미한 차이가 있는지 검정
• 분산을 통한 집단간의 차이 평가
• 집단 간 분산, 집단 내 분산으로 분해해 비교
  1. 집단 간 분산
     : 각 집단의 평균이 전체 평균으로부터 떨어진 정도
     : 집단 간 차이 ∝ 집단 간 분산
  2. 집단 내 분산
     : 각 집단 내부 데이터가 내부 평균으로부터 퍼진 정도

F-통계량
귀무가설 : 모든 집단의 평균은 동일
대립가설 : 적어도 한 쌍의 집단 평균은 다름

if F > 1 : 귀무가설 기각

4. 다변량 분산 분석

: 측정형 변수, 종속 변수가 2개 이상
: 독립 변인의 수가 2개

공분산과 독립성 관계

공분산 : 2개의 확률 변수의 상관 정도

• 두 확률 변수가 상호 독립(Cov(A, B) = 0) = 공분산 0
  △ Cov(A, B) = 0이라고 해서 A, B가 상호 독립은 아님

두 확률 분포 간 독립성 확인

1. 분포 독립성 확인
   : 두 확률 변수의 결합 확률 분포를 확인
   • P(X, Y) = P(X) x P(Y) = 상호 독립

2. 공분산 및 상관계수 확인
   : 공분산 = 0 and 상관계수 = 0, X, Y 독립

3. 독립성 검정
   : 카이제곱 독립성 검정법 등

변수 축약

• 변수들 상관 관계를 통한 변수의 수 감소

1. 주성분 분석 (PCA)
   : 다변량 자료에서 비정규성/이상치 발견
   : 상관 관계 없는 새로운 변수 도출
   : N개의 변수 → 서로 독립인 K개의 주성분 도출
   • 원 변수의 차원 감소 ∵ K < N

2. 요인 분석
   : 변수 간 상관 관계 분석 → 요인Factor 기반 공통차원을 통해 축약
   : 독립/종속 변수 개념 X

3. 정준 상관 분석
   : 정준 변수 = 집단 간 상관 구조를 가장 잘 설명하는 변수 간 선형 결합
   : 정준 상관 계수 = 정준 변수 간 상관 계수
   : 두 집단 중 변수의 수가 적은 집단의 변수 수 만큼의 정준 변수 도출

개체 유도

• 개체 특성을 측정한 변수 간 상관 관계를 통해 유사 개체 분류

1. 군집 분석 : Cluster Analysis
   : 모집단에 대한 사전 정보 X
   : 관측값 간의 유사성(거리) 이용

   군집 분석 방식 구분

   1. 계층적 군집 분석
      : 차례로 군집화, 한 번 병합되면 분리하지 않음
   2. 비계층적 군집 분석
      : 산포 측도 이용, 재분류 가능
   3. 조밀도
      : 데이터 분포 특성에 따라 군집화
   4. 그래프
      : 시각적 군집화(2, 3차원으로 축소 필수)

2. 다차원 척도법 : MDS
   : 다차원 개체 간 거리 / 비유사성 활용해 낮은 차원에 위치시킴
   • 개체 간 구조, 관계 파악 용이

3. 판별 분석
   : 많은 그룹으로 나누어진 개체에 대해 분류에 영향을 미칠 특성 측정
   • 새로운 개체 분류
   • 로지스틱 판별 분석
     : 분류 판별식으로 로지스틱 회귀 분석을 이용

---

3. 비정형 데이터 탐색

• 정의된 데이터 모델이 없음.
• 텍스트, 날짜, 숫자, 사실 등
• 특징을 추출해 정형/반정형으로 변환

비정형 데이터 분석

1. Data Mining
   : 대규모 데이터에서 통계적 규칙, 패턴을 분석해 가치있는 정보 추출
   : 탐색적 자료분석, 가설 검정, 시계열 분석 등
   : OLAP, SOM, 신경망 등의 기술적 방법론 사용

   • 적용 분야
     : 신용 평가 모델, 장바구니 분석등
     : Classification, Clustering, Association, Sequencing, Forecasting
   • 단점
     : 자료 의존성 높음
     : 자료가 현실에 대한 반영도가 낮다면 모형이 잘못됨

2. Text Mining
   : NLP를 통해 데이터의 숨겨진 의미 발견

3. Opinion Mining
   : 사람의 주관적 의견을 통계/수치화 → 객관적 정보
   : NLP를 통해 감정 및 뉘앙스, 태도를 파악

4. Web Mining
   : 웹 자원으로부터 유의미한 패턴 및 추세 도출
   : log, User Action 등을 마케팅에 사용

   1. 웹 구조 마이닝 : 구조적 요약 정보
   2. 웹 내용 마이닝 : 유의미한 Contents
   3. 웹 사용 마이닝 : 유저 액션 등의 패턴