[빅데이터분석기사] Part2 - CH 01. 데이터 전처리 (2)

Section 02. 분석 변수 처리

1. 변수 선택

• 독립 변수를 효율적으로 선택하는 과정

변수별 모형

1. 전체 모형 FM : 모든 독립 변수 사용
2. 축소 모형 RM : 전체 모형에서 사용되는 변수의 수 감소
3. 영 모형 NM : 사용하는 독립변수 0개

변수 선택 방법

1. 전진선택법 : NM에서 시작, 중요 변수를 차례로 모형에 포함(한 번 추가된 변수는 제거 X)
   => 부분 F검정을 통한 유의성 검증

2. 후진선택법 : FM에서 시작, 설명력이 낮은 변수 순으로 제거
   => 부분 F검정을 통한 유의성 검증

3. 단계적선택법 : 전진선택법을 통한 유의미 변수 포함 → 포함되지 않은 나머지 변수에 후진선택법 적용해 제거

---

2. 차원축소

• 차원 : 데이터 종류의 수
• 차원축소 : 데이터 종류(변수)의 양 감소

차원축소의 필요성
1. 복잡도 축소 : 동일 품질 보장 하에, 효율성 향상
2. 과적합 방지 : 차원 증가 → 과적합 가능성 ↑ → 분석 모형에 대한 신뢰도↓
3. 해석력 확보 : 차원의 수 ∝ 분석 모델 내부 구조의 복잡성
4. 차원의 저주 : 학습 데이터 수 ＜ 차원 수 => 성능 감소

차원축소 방법

1. 요인 분석 : Factor Analysis

• 변수들 간의 상관관계 분석을 통해 공통 차원 축약, 통계 분석 과정 수행

• 주성분 분석, 공통요인 분석, 특이값 분해(SVD)행렬, NMF 등

• 목적
  : 변수 축소 및 제거
  : 관련 변수들의 군집화를 통한 변수 특성 파악(상호 독립성 파악 용이)
  : 변수의 독립성 여부 파악을 통한 타당성 평가
  : 요인 점수를 이용한 신규 변수 생성(파생변수)

• 특징
  : 기술 통계에 의한 방법
  : 독립/종속 변수 개념이 없다.

2. 주성분 분석 : PCA

• 데이터의 특성을 설명 가능한 하나 이상의 특징 도출

• 고차원 공간 데이터 → 직교 변환 → 저차원
  : 각 고차원 데이터 간 상호 연관성 O

• 원 데이터의 중요 정보를 최대한 보존하면서 차원 축소를 목표

• PC1 : 첫번째 주성분
  : 데이터 분산을 가장 많이 설명하는 방향

• PC2 : 두번째 주성분
  : PC1과 직교 & 남은 분산을 가장 많이 설명하는 방향

3. 특이값 분해 : SVD

• m x n 행렬 A 를 3개의 행렬 곱으로 분해
  

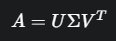
  • U : m x m 크기의 직교 행렬
  • Σ : m x n 크기의 대각 행렬
  • Vt : n x n 크기의 직교 행렬, V의 전치 행렬

• 데이터의 주요 정보가 큰 특이값(k)에 집중

• 적당한 특이값 k를 통해 비슷한 정보력의 차원으로 축소

4. 음수 미포함 행렬 분해 : NMF

• 음수 미포함 행렬 V를 음수 미포함 2개 행렬(W, H)의 곱으로

• 데이터가 0 이상 값으로 구성되어있을 때, 데이터의 숨겨진 구조/패턴 도출

• W, H의 차원은 V보다 작다.

---

3. 파생 변수의 생성

• Data Mart
  : Data Warehouse로부터 수집(복제)된 데이터 모임의 중간층
  : 요약 변수 + 파생 변수

파생 변수

: 기존 변수나 데이터로부터 새로운 규칙, 계산을 적용해 만든 변수
: 모델의 성능 향상 및 데이터의 숨겨진 의미 파악에 사용
: 주 구매매장, 주 활동지역 등
: 매우 주관적, 논리적 타당성 필요

국어, 수학 점수 데이터를 통한 종합적 학업 능력 평가 시,
전체 과목 평균 = 파생 변수

• 유의점
  : 전 데이터 구간에 대한 대표성을 가져야 함

교호작용 : Interaction

• 한 변수의 효과가 다른 변수의 값에 따라 달라지는 현상

  광고비와 할인율 두 변수의 상호작용 ▶ 매출이라는 결과 변수에 영향

• 교호작용을 통한 파생변수 생성
  : 2개 이상 변수가 서로에게 영향을 미쳐 예측 변수에 미치는 효과가 달라질 떄, 이를 확인하기 위해 새로운 변수를 만드는 기법
  : 독립 변수 간의 상호작용을 모델에 반영
  ※ 단, 종속 변수와 독립 변수 간 교호작용을 사용하면 안됨

요약 변수

: 수집된 정보를 분석에 맞게 종합
: Data Mart에서 가장 기본적인 변수
: 다른 분석 모델에서 공통으로 사용 가능한 변수
: 매장이용 횟수, 기간별 구매금액 등

• 유의점
  : 결측치, 이상치 처리에 유의
  : 연속형 변수 → 구간화를 통해 의미있는 구간 발굴

---

4. 변수 변환

• 데이터를 분석하기 좋은 형태로 변환
  • 데이터 전처리 중 일부

변환 방법

1. 범주형 변환

• 변수를 범주형으로 변환(순위, 비율 % )
• 결과의 명료성 / 정확성 향상

2. 정규화

• 연속형 데이터를 상대적 특성이 반영된 데이터로 변환

  1. 일반 정규화
     : 수치상 차이를 같은 범위로 변환
  2. Min-Max 정규화
     : 0 ≤ value ≤ 1
     : 이상치 영향↑
  3. Z-Score
     : 이상치 문제를 해결
     : 평균 = 0, value < AVG = 음수

3. 로그 변환

• 기존 수치값 X에 log를 씌워(ln(X)) 분포가 정규 분포에 가까워짐
• 데이터가 좌측으로 치우친 경우에 사용

4. 역수 변환

• 변수 X의 역수(1/X)를 분석에 사용해 선형적 특성 향상
• 극단적 좌측 치우침의 데이터 분포를 정규화

5. 지수 변환

• 변수 X에 대한 지수 사용(X^n)해 선형적 특성 향상
• 극단적 우축 치우짐의 데이터 분포를 정규화

6. 제곱근 변환

• 변수 X에 대해 제곱근(√X) 사용
• 좌측으로 약간 치우친 데이터 분포에 사용
  ↔ 우측으로 약간 치우쳤다면 X^2

단일 집단의 정규성 검정 방법
1. 샤피로 테스트
2. Q-Q Plot

7. `Box-Cox 변환

• 데이터 분포를 정규분포에 가깝게, 분산의 안정성 확보
• λ(변환 형태 결정)에 따라 형태가 상이한 거듭제곱 변환
  
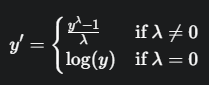
• 모든 실수에서 연속
• 오른쪽으로 치우친 분포를 가질 때 사용

---

5. 불균형 데이터 처리

Class 불균형

• 데이터에서 각 Class(범주형 반응 변수)별 데이터 양 차이가 클 때
• 불균형도가 높은 High-Imbalanced Data의 경우,
  Class가 우세한 모형의 정확도가 높다.
  => 성능 판별이 어렵다.

불균형 데이터 처리 방법

1. 가중치 균형법 : Weight Balancing

• 소수 Class에 더 큰 가중치 부여 → 소수 Class를 잘못 예측 시, 더 큰 Penalty
• Data sample 수 변경 없이 학습 과정에 개입

2. UnderSampling

• 다수 Class 中 일부만 사용 (대표성 고려)

3. OverSampling

• 소수 Class의 데이터를 복사해 절대적인 수 증가

---

6. Encoding

• 범주형 데이터 → 숫자 의 변환 과정

Label Encoding

• 각 범주에 고유한 정수값 할당
• 데이터 차원 증가가 없어, 메모리 사용량이 적음
• 변환 숫자들 간의 순서(Ordinality)가 발생
• 순서 있는 데이터에 사용 or 트리 기반 데이터

One-Hot Encoding

• 각 범주를 별도의 binary로 변환
• 해당하는 인덱스 1, 아니면 0
• 범주 종류 수 ∝ 차원의 저주
• 순서 없는 명목형 데이터에 주로 사용

Target Encoding

• 각 범주를 해당 범주 결과 변수의 평균값으로 변환
• 분류 문제에서 사용
• new column 생성 X = 차원증가 문제 해결
• 과적합 가능(교차 검증, Smoothing 기법을 함께 사용해 방지)