Eigendecomposition

로렌조·2020년 6월 9일

deeplearningbook

목록 보기

1/1

수학에 나오는 숫자, 행렬 등은 어떤 특성을 가진 구성물로 쪼개졌을때 좀 더 잘 이해할 수 있다. 예를 들면 12를 그냥 12로 써서 표현할 때보다, 12 = 2 x 2 x 3 으로 표현했을 때, "12는 3으로 나눠진다" 또는 "12는 5로 나눠지지 않는다" 와 같은 식으로 더 많은 정보를 알 수 있게 된다.

비슷하게 행렬의 고유 특성을 파악하기 위해서 행렬을 분해하는 방법이 여러개가 있는데,
그 중 모든 행/컬럼이 linearly independent한 square matrix에 자주 쓰이는 분해 방법이 eigen decomposition이다.

Eigen vector와 eigen value?

✏️ 개념

\mathbf{A} \mathbf{v}=\lambda \mathbf{v}

행렬 $\mathbf{A}$ 가 square matrix일때, 위 식을 만족하는 벡터 $\mathbf{v}$ , 상수값 $\lambda$ 가 있으면,

$\mathbf{v}$ 는 $\mathbf{A}$ 의 eigen vector
$\lambda$ 는 $\mathbf{A}$ 의 eigen value

라고 정의 할 수 있다. 말로 풀어서 해석해본다면 "어떤 벡터 $\mathbf{v}$ 앞에다가 $\mathbf{A}$ 를 곱함으로써, 벡터 $\mathbf{v}$ 에 transformation $\mathbf{A}$ 를 취했는데, 벡터 $\mathbf{v}$ 에 상수값 $\lambda$ 를 곱한 값이랑 같아졌다"고 할 수 있다.

🤯 특성

square matrix만 eigen vector와 eigen value가 존재한다
m x m 크기의 매트릭스는 최대 m개의 eigen vector를 가진다
symmetric matrix(대칭 행렬)의 모든 eigen vector들은 서로 수직이다
일반적으로, eigen value와 eigen vector는 내림차순으로 큰거부터 정렬되고, eigen vector는 unit length로 표현한다. 이렇게 표현했을때, 모든 eigenvalue가 unique하면 아래에서 설명할 eigendecomposition 결과도 unique하다.

Eigendecomposition?

✏️ 개념

만약에 정말 운이 좋아서 행렬 $\mathbf{A}$ 가 자기 차원 수만큼 linearly independent한 eigen vector를 가지고 있다고 가정해보면,
(실제로는 그렇지 않은 경우가 더 많을 것이기 때문에 운이 좋다고 표현했다)

\mathbf{A} \mathbf{v_1}=\lambda_1 \mathbf{v_1}

\mathbf{A} \mathbf{v_2}=\lambda_2 \mathbf{v_2}

\mathbf{A} \mathbf{v_3}=\lambda_3 \mathbf{v_3}

...

가 $\mathbf{A}$ 의 차원 개수만큼 있을때, 저 식에서 벡터 $\mathbf{v_i}$ 들을 옆으로 이어붙인다고 하면,

\mathbf{A} \mathbf{V}=\mathbf{V} \operatorname{diag}(\mathbf{x})

로 나타낼 수 있고, $\mathbf{V}$ 는 역행렬이 존재한다. (행렬 $\mathbf{V}$ 를 구성하는 벡터들은 eigen vector이고, eigen vector끼리는 linearly independent하므로)

\mathbf{A} =\mathbf{V} \operatorname{diag}(\mathbf{\mathbf{\lambda}}) \mathbf{V}^{-1}

이다.

만약 여기서 $\mathbf{A}$ 가 "symmetric" matrix라면,

$\mathbf{V}$ 의 column vector들은 linearly independent하므로, 아래 식을 만족한다.
다른 말로는, 두 벡터 $\mathbf{v_i}$ , $\mathbf{v_j}$ 가 orthogonal하다고 한다.

\mathbf{v_i}^T\mathbf{v_j}=0

$\mathbf{V}$ 의 column vector들은 위에서 봤듯이 $\mathbf{A}$ 의 eigen vector인데,
보통 eigen vector를 아래처럼 normal vector로 표시한다. $\mathbf{v_i}^T\mathbf{v_i}=1$

즉, $\mathbf{V}$ 의 모든 column vector들은 서로 orthogonal하고, normal vector이기 까지 하므로, orthonormal 하다고 한다. 그리고, 이 orthonormal한 column vector로 이루어진 $\mathbf{V}$ 를 orthogonal matrix라고 한다.

주의 할 점은 orthonormal한 벡터들을 가진 행렬인데 orthonormal matrix라고 안하고 orthogonal matrix라고 한다는 것이다.

Eigendecomposition은 unique하지 않을 수 있다. 만약 같은 eigenvalue를 여러개 가지고 있다면, 즉 여러 eigen vector가 같은 eigen value를 공유할 경우 $\mathbf{V}$ 는 unique하지 않게 된다. (같은 eigen value를 가지는 $\mathbf{V}$ 의 column vector들의 순서는 어떻게 하든 성립)

🤬 이걸 배워 어디에 쓰나?

Matrix singularity

\mathbf{A}의 \ eigen value들 \ 중에 \ 0이 \ 있다. \Leftrightarrow \mathbf{A}는 \ singular \ matrix이다

Singular matrix는 역행렬이 존재하지 않는 행렬이다. 기본적으로 eigen value에 관련된 개념이라 이것도 특성으로 넣은 것 같다.

Quadratic expression optimization

$\mathbf{A}$ 가 real symmetric matrix라고 하고,

f(x)= x^{T} A x, \ subject \ to \ \|x\|_{2} = 1

라는 제약조건이 있는(constrained) 이차식(quadratic formula)이 있다고 하면,

$f$ 는 $x$ 가 $\mathbf{A}$ 의 eigen value들 중, 가장 큰 eigen value에 대응하는 eigen vector일때 최대값을 갖는다.
$f$ 는 $x$ 가 $\mathbf{A}$ 의 eigen value들 중, 가장 작은 eigen value에 대응하는 eigen vector일때 최소값을 갖는다.

Positive definite

행렬 $\mathbf{A}$ 의 모든 eigen value가 양수면, 행렬 $\mathbf{A}$ 를 positive definite라고 한다.
행렬 $\mathbf{A}$ 의 모든 eigen value가 양수 또는 0이면, 행렬 $\mathbf{A}$ 를 positive semidefinite라고 한다.
행렬 $\mathbf{A}$ 가 positive definite/semidefinite이면, 모든 벡터 $\mathbf{x}$ 에 대해, 아래를 만족한다.

\mathbf{x^T} \mathbf{A} \mathbf{x} \ge 0

행렬 $\mathbf{A}$ 가 positive definite일 경우에는, 추가로 아래가 성립한다.

\mathbf{x^T} \mathbf{A} \mathbf{x} = 0 \Rightarrow \mathbf{x}=0

Positive definite특성을 사용하는 대표적인 예시로, 차원(dimension)보다 데이터 포인트 개수가 더 많을 때의 least square regression 문제를 보자. 이 경우에는 $\mathbf{A}$ 의 column벡터들이 linearly independent해도, $\mathbf{b}-\mathbf{A} \mathbf{x} = 0$ 이 성립할 수 없다. 그래서 least square error를 최소화 하는 파라미터 $\mathbf{x^*}$ 를 찾아야 한다.

\min _{\mathbf{x^*}} \|\mathbf{b}-\mathbf{A} \mathbf{x}\|^{2} \\

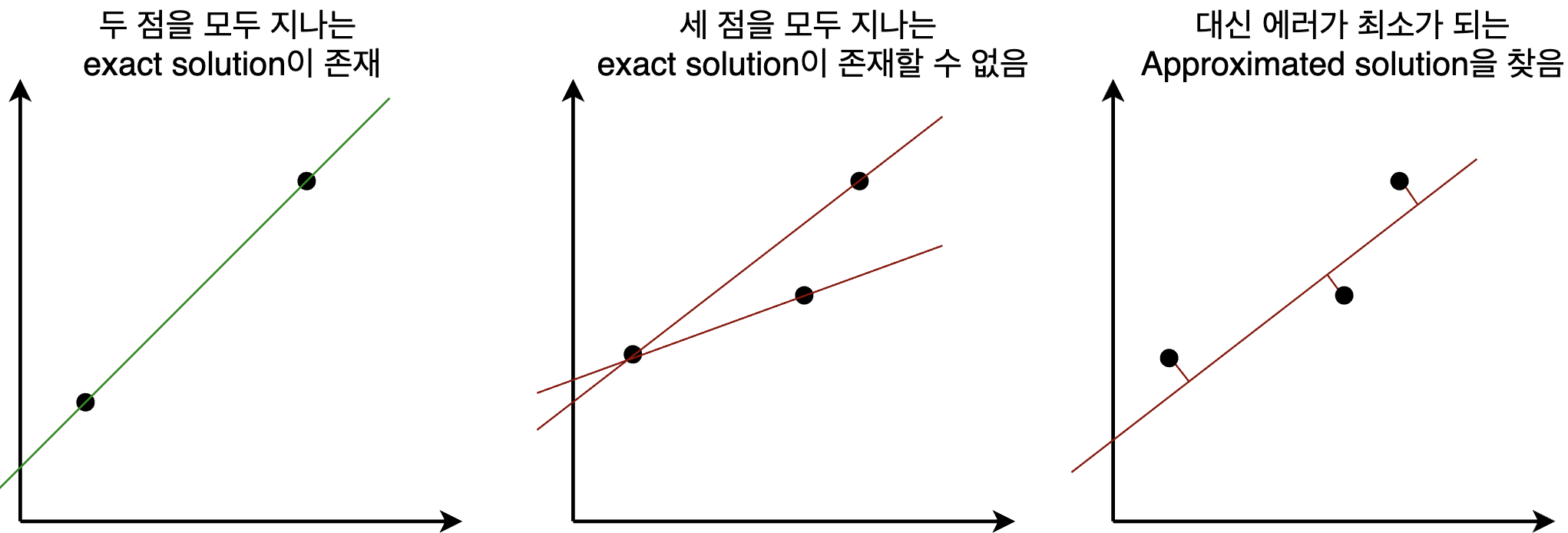
위의 식을 미분했을 때 0이 되는 $\mathbf{x^*}$ 를 찾기 위해, 아래와 같이 식을 정리할 수 있다.

\begin{aligned} & \min _{\mathbf{x^*}}\left\{E(\mathbf{x})=(\mathbf{b}-\mathbf{A} \mathbf{x})^{\top}(\mathbf{b}-\mathbf{A} \mathbf{x})\right\} \\ =& \min _{\mathbf{x^*}}\left\{\mathbf{b}^{\top} \mathbf{b}-2 \mathbf{x}^{\top} \mathbf{A}^{\top} \mathbf{b}+\mathbf{x}^{\top} \mathbf{A}^{\top} \mathbf{A} \mathbf{x}\right\} \\ \rightarrow & \frac{\partial E(\mathbf{x})}{\partial \mathbf{x}}=0 \\ \rightarrow &-2 \mathbf{A}^{\top} \mathbf{b}+2 \mathbf{A}^{\top} \mathbf{A} \mathbf{x^*}=\mathbf{0} \\ \rightarrow & \mathbf{A}^{\top} \mathbf{A} \mathbf{x^*}=\mathbf{A}^{\top} \mathbf{b} \end{aligned}

여기서 만약 $\mathbf{A}$ 의 column vector들이 linearly independent하면, $\mathbf{A^T}\mathbf{A}$ 가 positive definite이고, $\mathbf{A^T}\mathbf{A}$ 의 역행렬이 존재한다. (Eigendecomposition과 matrix orthogonality를 이용하면 쉽게 증명이 가능하다)
그러면 approximated solution인 $\mathbf{x^*}$ 를 구할 수 있게 된다.

Reference

로렌조

한탕을 꿈꾸는 대학원생

1개의 댓글

Jio

2020년 6월 25일

ㅠㅠㅠ 좋은 글 잘 보고 갑니다..!

답글 달기