Priority Queue & Heap

• 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료 구조

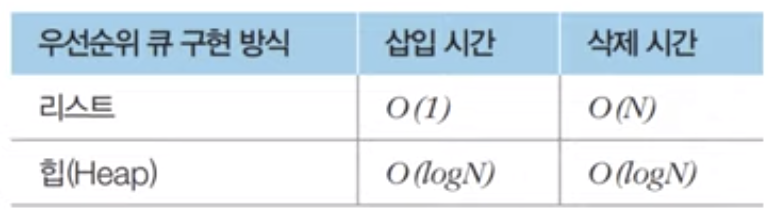
• list와 prioirty queue의 시간 복잡도 비교 내용
• 단순 N개 데이터를 힙에 넣었다가 꺼내는 작업은 정렬과 동일 (힙정렬)
  • O(NlogN)

Heap 특징

• 완전 이진 트리 자료구조의 일종
  • 완전 이진 트리 : 루트 노드부터 왼쪽 자식, 오른쪽 자식 노드 순서대로 데이터가 차례대로 삽입되는 트리
• 힙에서는 항상 루트 노드를 제거
• 최소 힙
  • 루트 노드가 가장 작은 값
  • 가장 작은 데이터가 우선적으로 제거
• 최대 힙
  • 루트 노드가 가장 큰 값
  • 가장 큰 데이터가 우선적으로 제거

Min-Heapify()

• 상향식

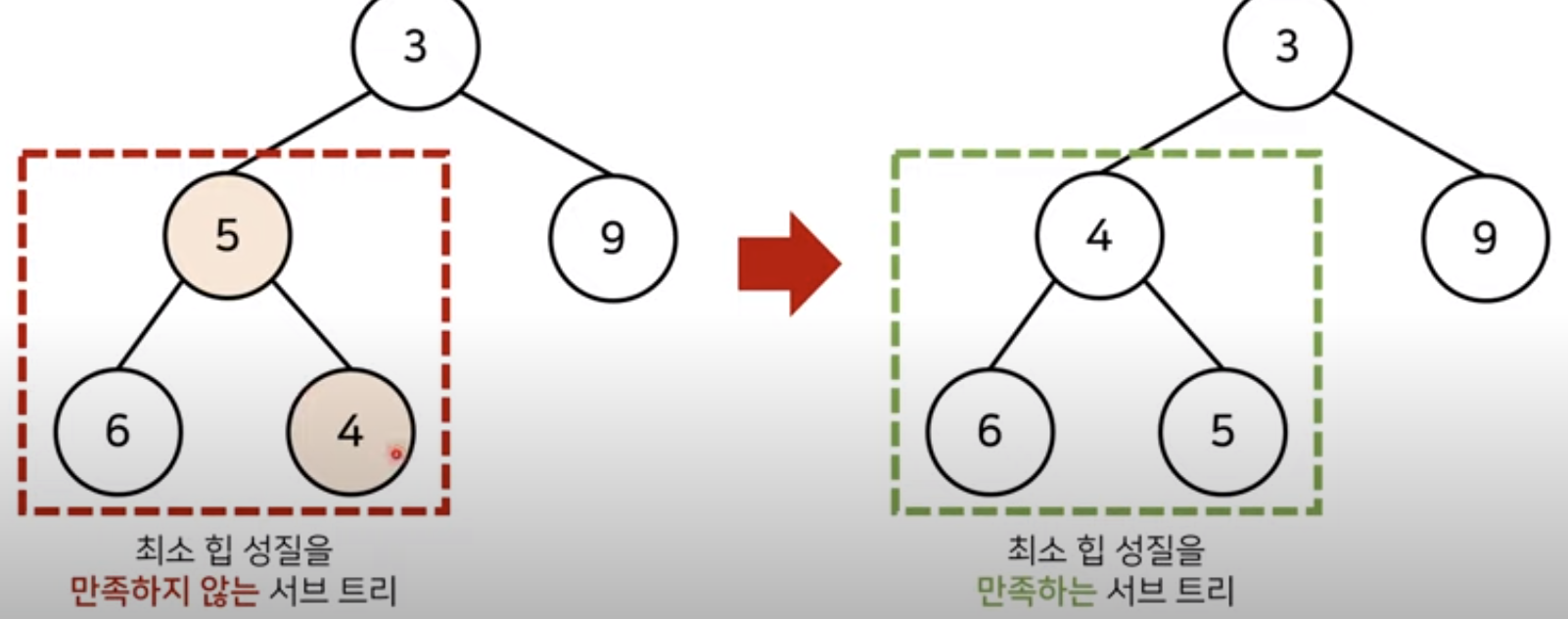
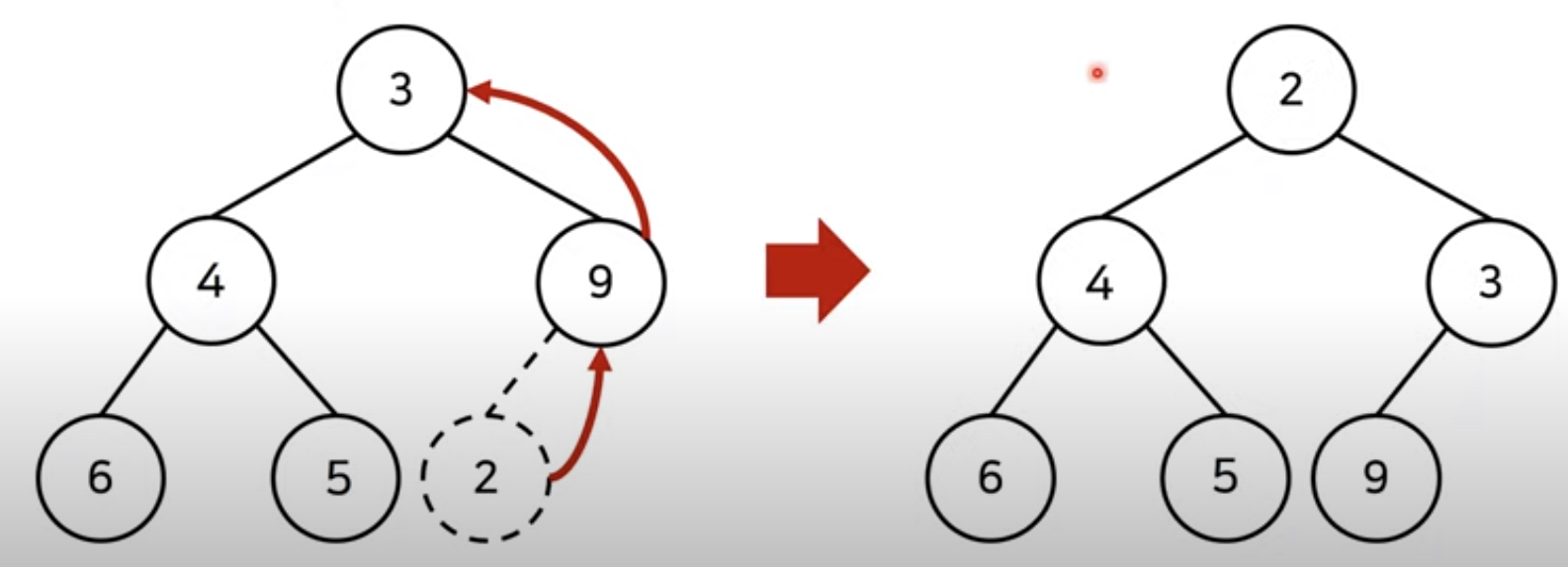
• 부모 노드로 거슬러 올라가며 부모보다 자신의 값이 더 작은 경우 위치를 교체
• 새로운 원소가 삽입되었을 때 O(logN)의 시간 복잡도로 힙 성질을 유지하도록 할 수 있다.

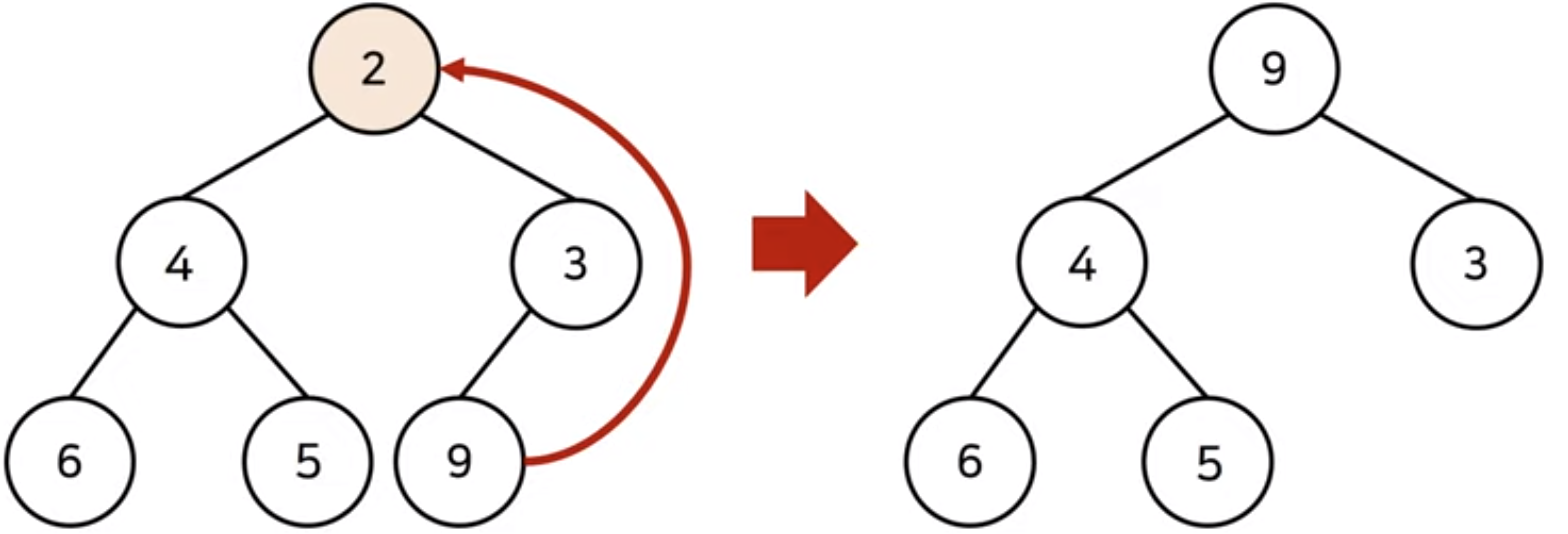
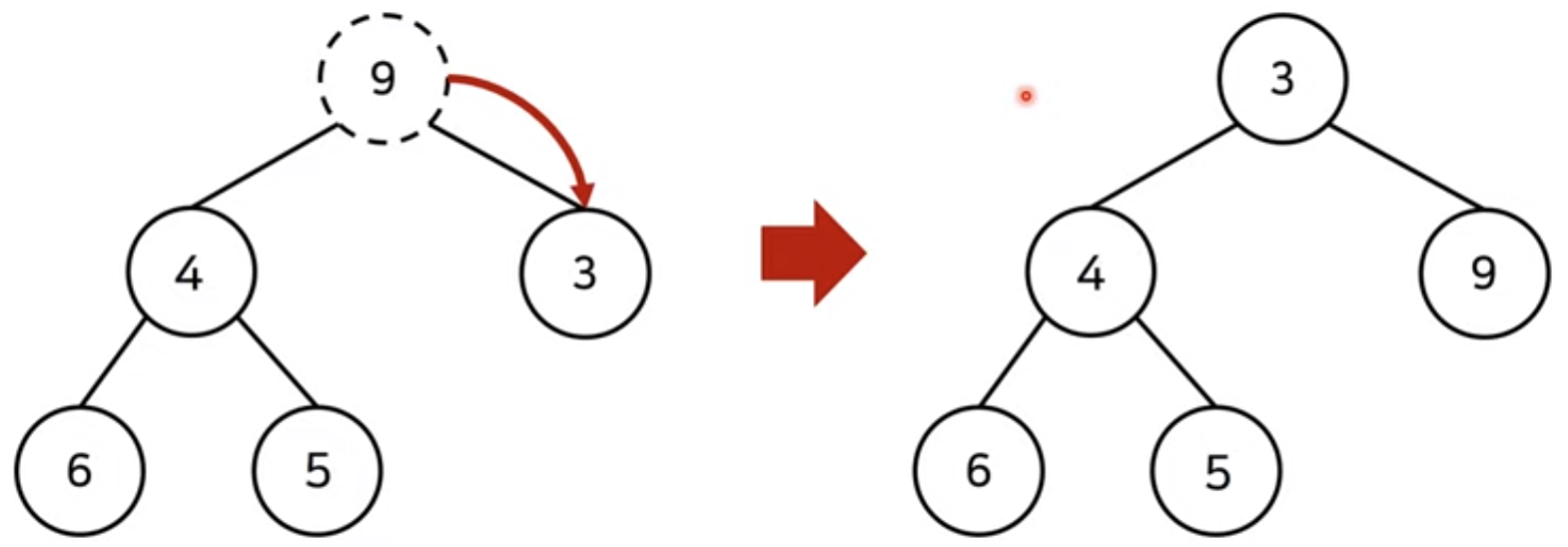
• 원소 제거 시에도 O(logN)
  • 가장 마지막 노드가 루트 노드의 위치에 오도록 한다.
  • 그 이후 하향식으로 더 작은 자식 노드로 Heapify() 진행

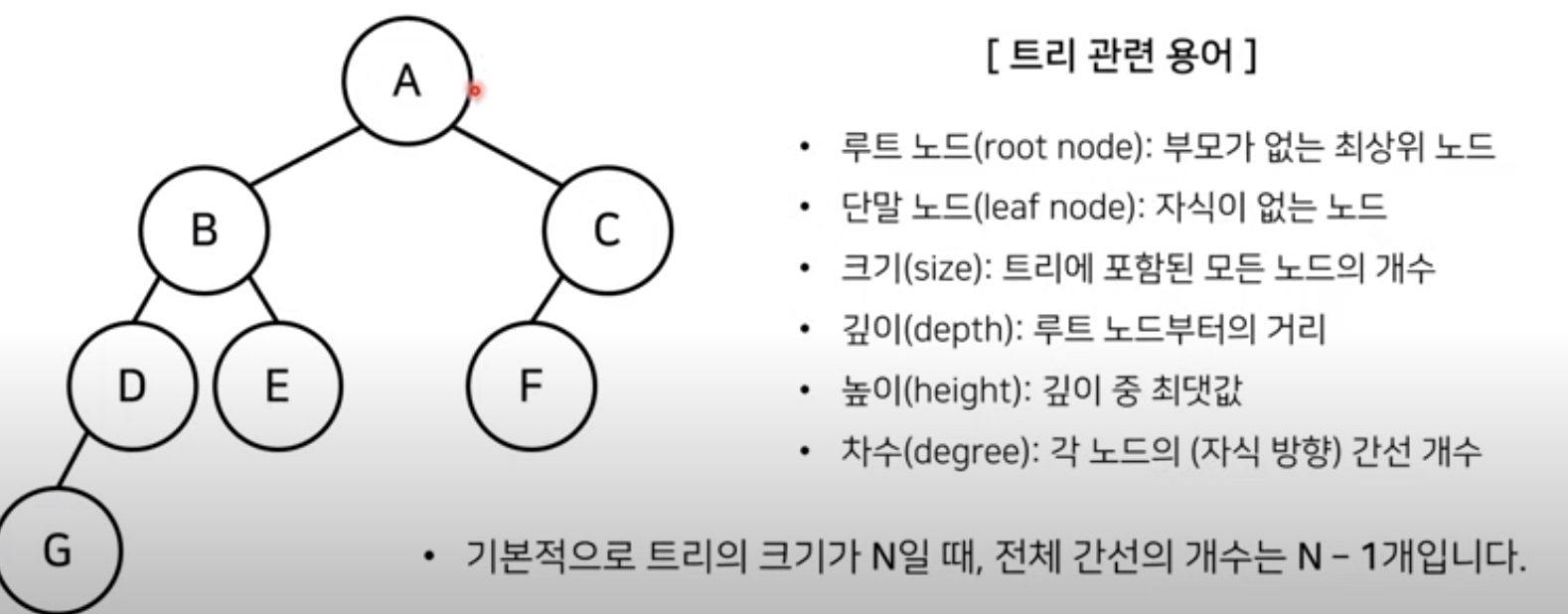
Tree

• 가계도와 같은 계층적 구조를 표현할 때 사용할 수 있는 자료 구조

이진 탐색 트리

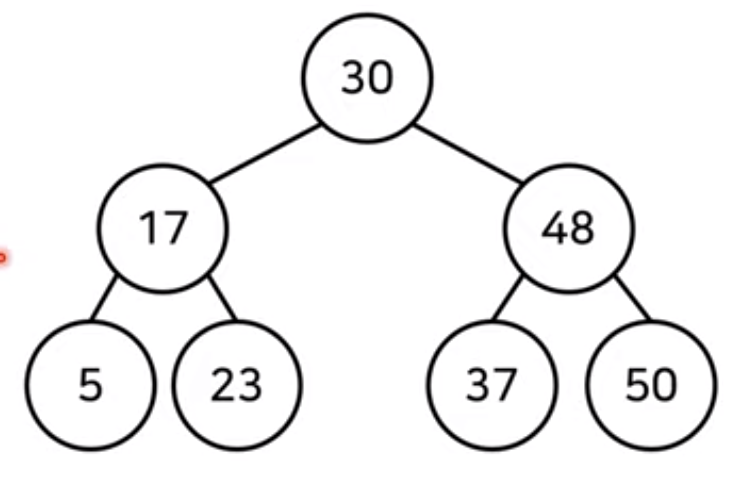
• 이진 탐색 트리 특징 : 왼쪽 노드 < 부모 노드 < 오른쪽 자식 노드
• 1. 루트 노드부터 방문 하여 탐색 진행
• 2. 찾는 원소가 더 작으면 왼쪽 자식노드, 더 크면 오른쪽 자식 노드로 방문
• 3. 현재 노드와 값을 비교 후 찾으면 탐색 종료

트리 순회

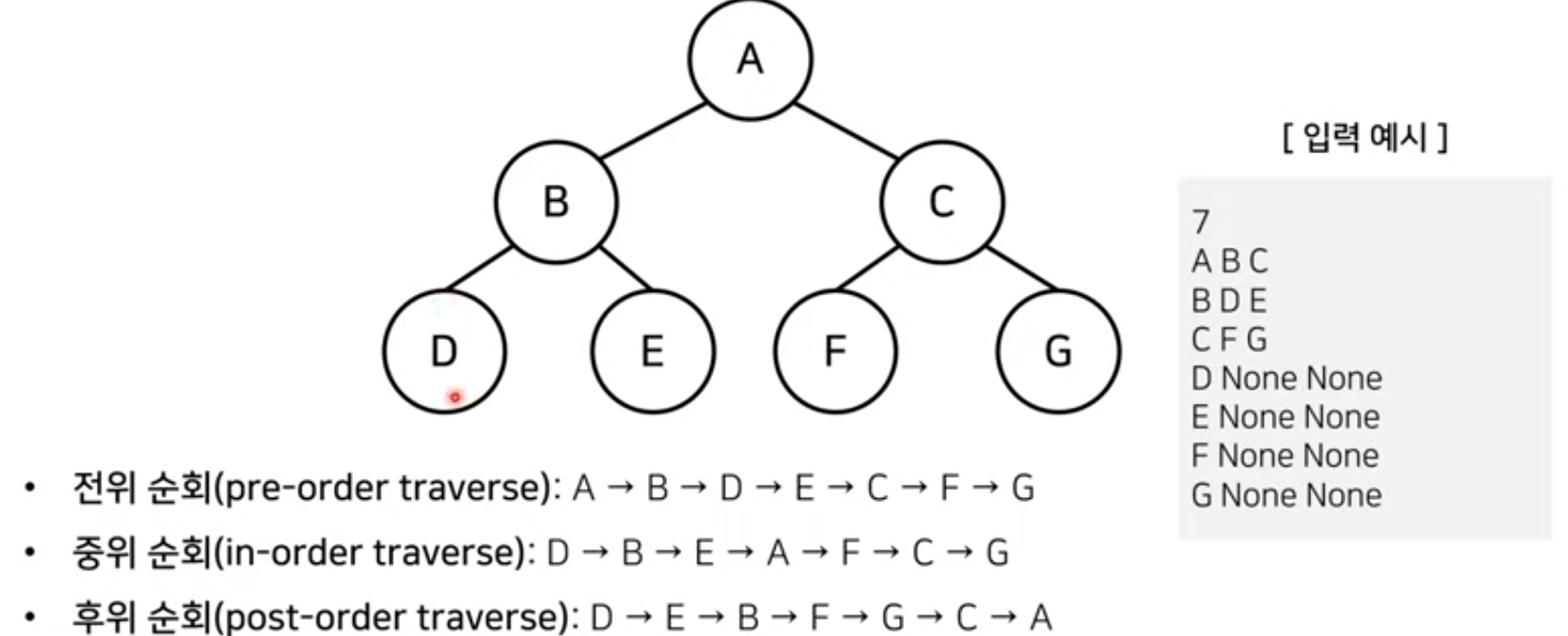
• 전위 순회 : 루트 먼저 방문
• 중위 순회 : 왼쪽 자식 방문 뒤 루트 방문
• 후위 순회 : 오른쪽 자식 방문 뒤 루트 방문

class Node:
	def __init__(self, data, left_node, right_node):
    	self.data = data
        self.left_node = left_node
        self.right_node = right_node

n = int(input())
tree = {}

for i in range(n):
	data, left_node, right_node = intput().split()
    if left_node == "None":
    	left_node = None
	if right_node = "None":
    	right_node = None
	tree[data] = Node(data, left_node, right_node)

벨만 포드 알고리즘

음수 간선이 포함된 상황에서 최단거리 문제

• 그래프에서 음수 간선의 순환이 포함된 경우 최단 거리가 음의 무한인 노드가 발생할 수 있다.
• 벨만 포드는 음의 간선이 포함된 상황에서도 사용할 수 있다.
  • 음수 간선의 순환을 감지할 수 있다.
  • O(VE)로 다익스트라 알고리즘에 비해 느리다.
• 1. 출발노드 설정
• 2. 최단 거리 테이블 초기화
• 3. 다음 과정 N-1번 반복
  • 1. 전체 간선 E개를 하나씩 확인
  • 2. 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
• 만약 음수 간선 순환이 발생하는지 체크하고 싶으면 3번 과정을 한 번 더 수행한다.
  • 최단 거리 테이블이 갱신되면, 음수 간선 순환이 존재하는 것이다.
• 다익스트라는 매번 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택한다. 음수 간선이 없다면 최적의 해를 찾을 수 있다.
• 벨만 포드는 매번 모든 간선을 전부 확인한다. 그러므로 다익스트라 최적의 해를 항상 포함한다. 하지만 간선을 전부 보므로 다익스트라보다 오래걸리지만 음수 간선 순환을 탐지할 수 있다.

import sys
input = sys.stdin.readline
INF = int(1e9)

def bf(start):
	dist[start = 0
    for i in range(n):
    	for j in range(m):
        	cur = edges[j][0]
            next_node = edges[j][1]
            cost = edge[j][2]
            
            if dist[cur] != INF and dist[next_node] > dist[cur] + cost:
            	dist[next_node] = dist[cur] + cost
                if i == n - 1: # n 번째 라운드에서도 값이 갱신되면 음수 순환 존재 
                	return True
	return False
    
n, m = map(int, input().split())
edges = []
dst = [INF] * (n+1)

for _ in range(m):
	a, b, c = map(int, input().split())
    edges.append((a, b, c) # a노드에서 b노드로 가는 비용이 c

negative_cycle = bf(1)

if negative_cycle:
	print("-1")
else:
	for i in range(2, n + 1):
    	if dist[i] == INF:
        	print('-1')
	else:
    	print(dist[i])

biary indexed Tree (잘 모르겠음)

• 데이터 업데이트가 가능한 상황에서 구간합 문제
• fenwick tree 라고도 한다.
• 2진법 인덱스 구조를 통해 구간합 문제를 효과적으로 해결해준다.
• 특정 숫자 K 0이 아닌 마지막 비트를 찾는 방법은 K & -K 연산을 하면된다.

• 대부분의 컴퓨터는 2의 보수를 따른다.
  • (-)는 모두 반전 후 1을 더한다.

n = 8

for i in range(n+1):
	print(i, '의 마지막 비트:', (i & -i))

트리구조 만들기

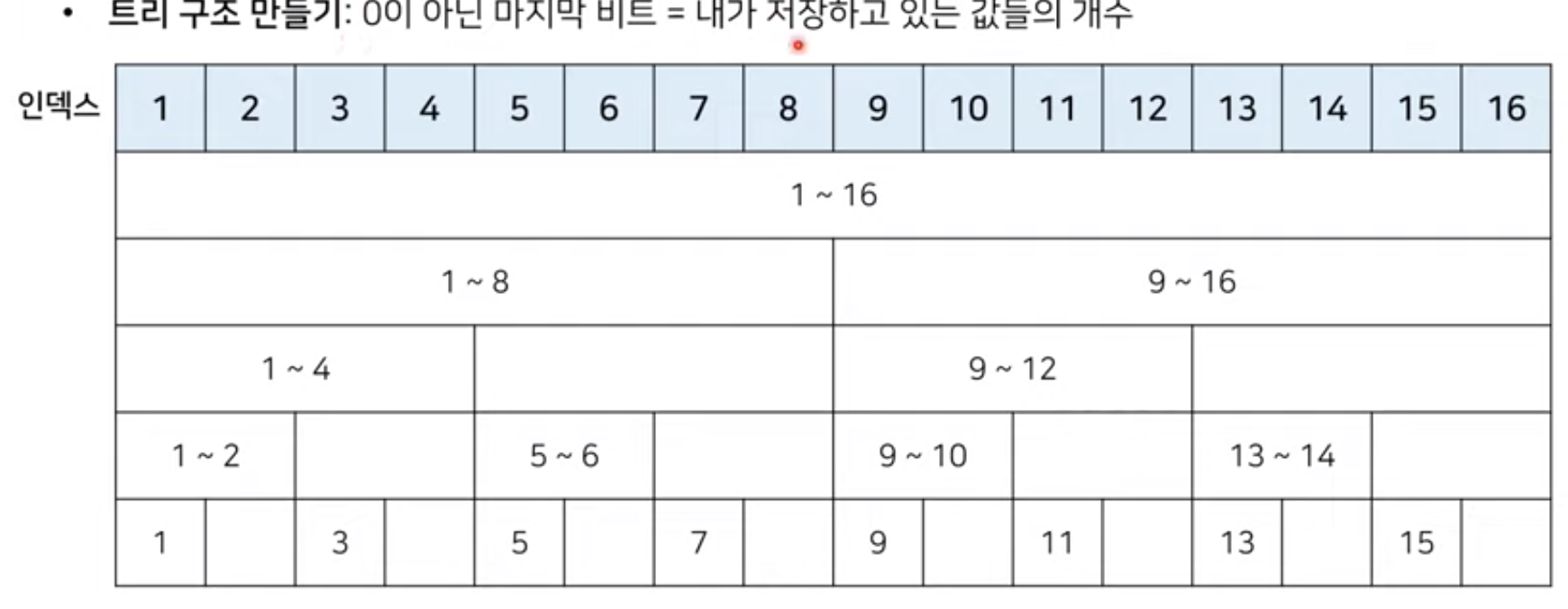
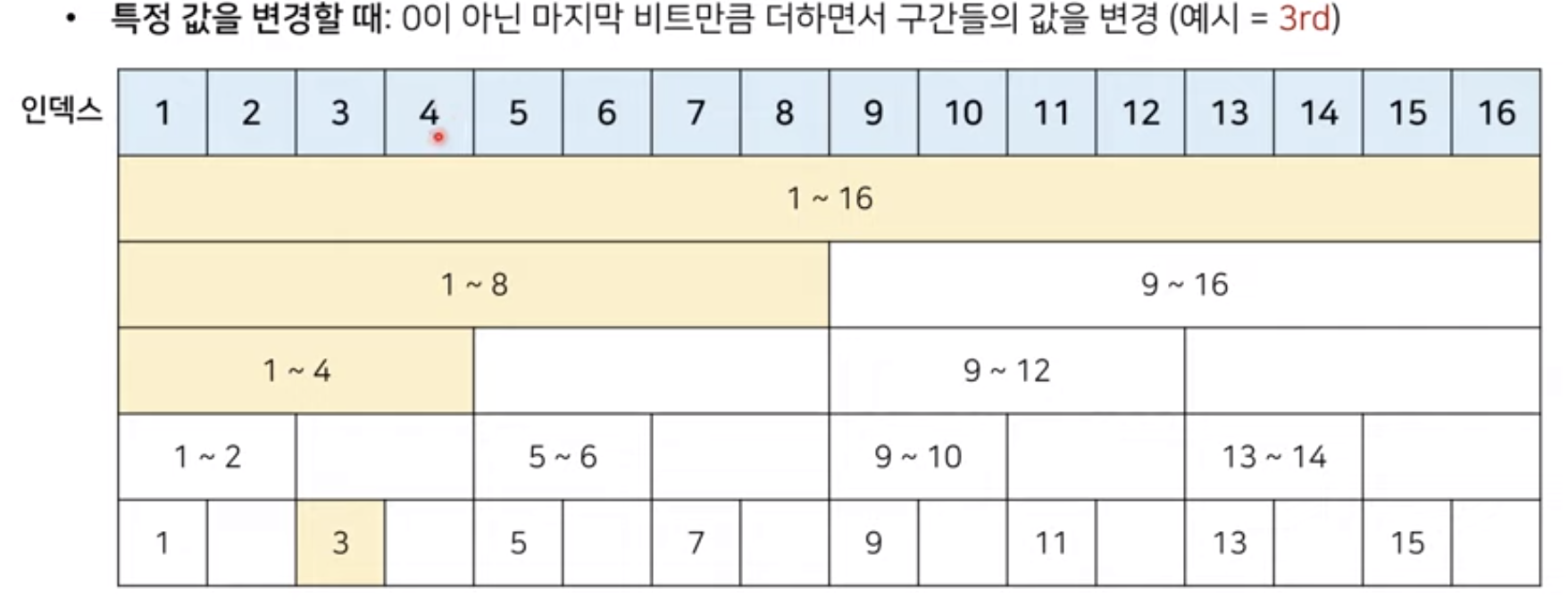
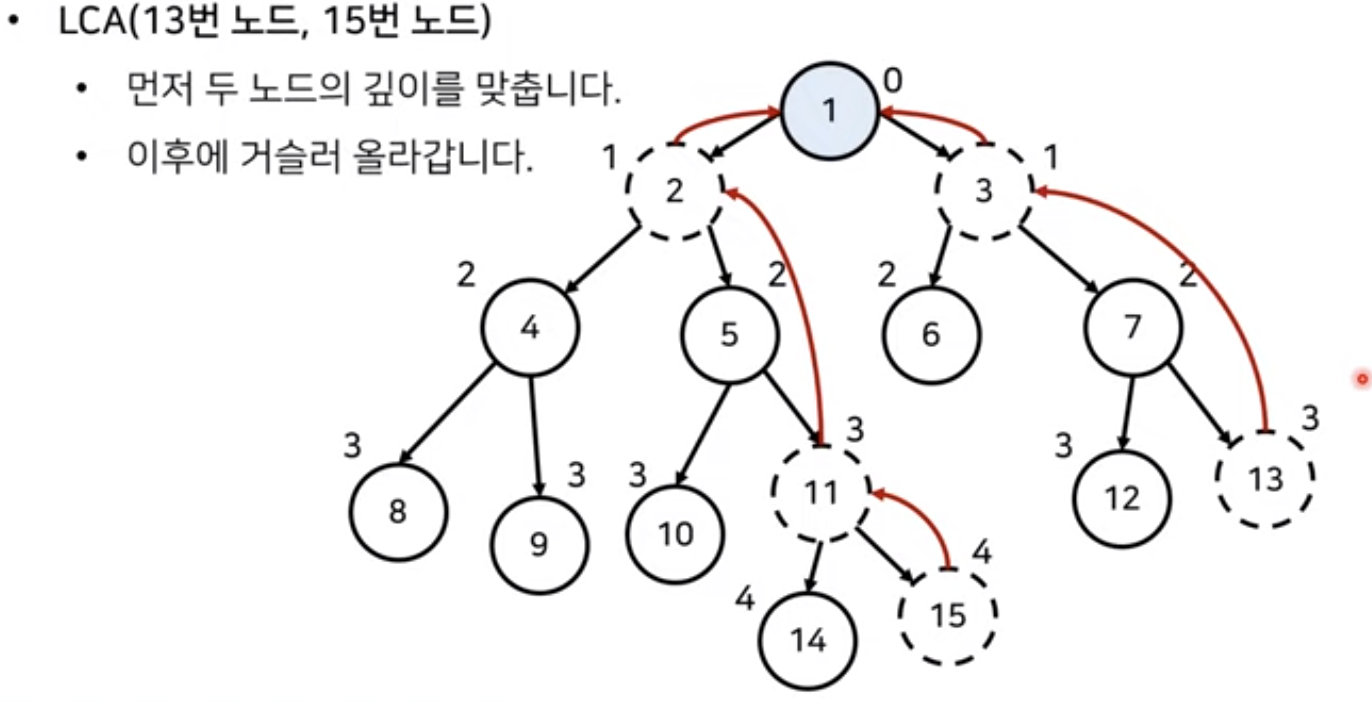
최소 공통 조상 (Lowest Common Ancestor)

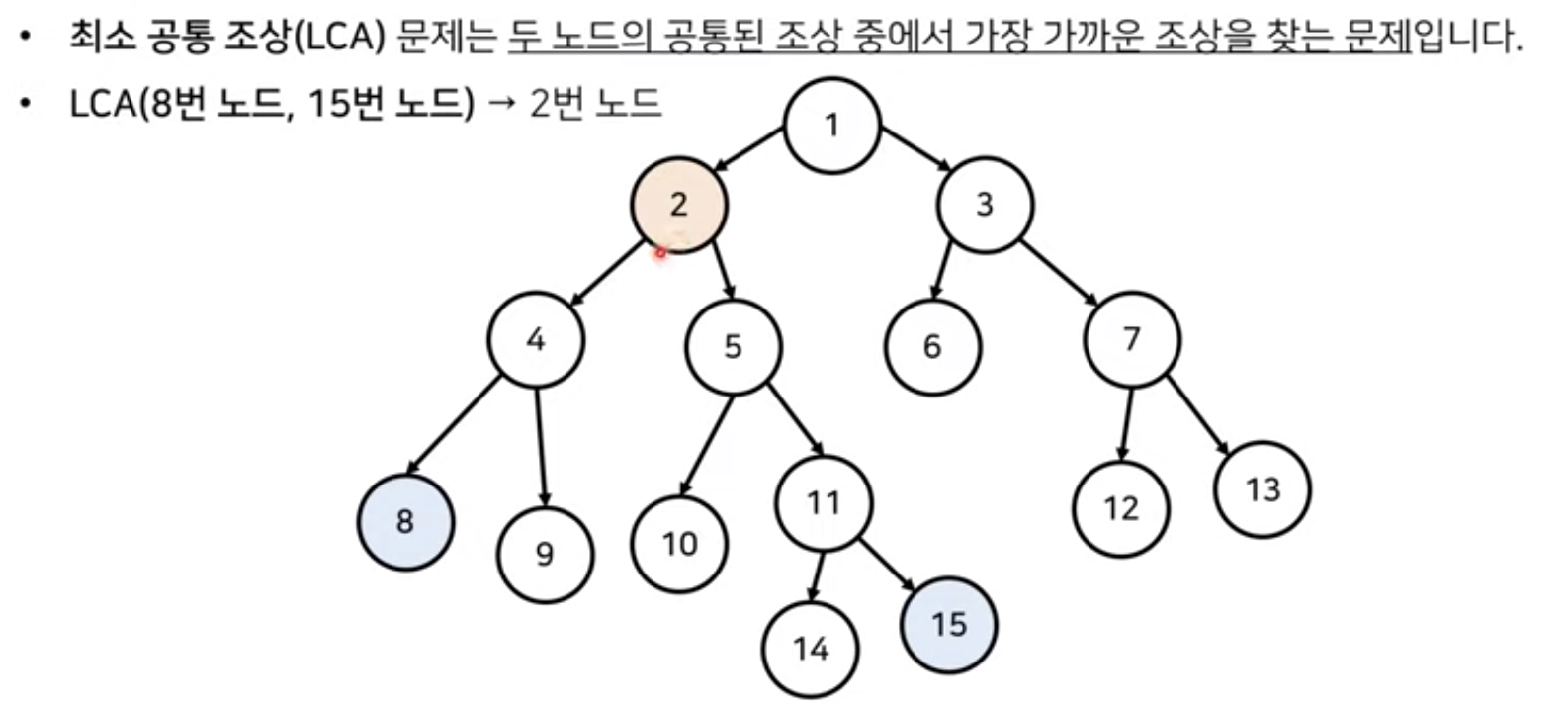
• 1. 모든 노드에 대한 깊이 계산
  • DFS 이용
• 2. 최소 공통 조상을 찾을 두 노드를 확인
  • 먼저 두 노드 깊이가 동일하도록 거슬러 올라간다.
  • 이후 부모가 같아질 때까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라간다.
• 3. 모든 LCA(a, b) 연산에 대해 2번 과정 반복

...

parnet = [0] * (n + 1)
d = [0] * (n+1) # 각 노드까지 깊이
c = [0] * (n+1) # 각 노드 깊이가 계산되었는지 여부
graph = [[] for _ in rnge(n+1)]

for _ in range(n - 1):
	a, b = map(int, input().split())
    graph[a].append(b)
    graph[b].append(a)
    
def dfs(x, depth):
	c[x] = True
    d[x] = depth
    for y in graph[x]:
    	if c[y]:
        	continue
            
		parent[y] = x            
    	dfs(y, depth + 1)

def lca(a, b):
	# 먼저 Depth가 동일하도록
	while d[a] != d[b]:
    	if d[a] > d[b]:
        	a = parent[a]
        else:
        	b = parent[b]
	
    # 노드가 같아지도록
	while a != b:
    	a = parent[a]
        b = parent[b]
	
    return a
    
dfs(1, 0) # 루트 노드는 1번 노드

m = int(input())

for i in range(m):
	a, b = map(int, input().split())
    print(lca(a, b))

• 매 쿼리마다 부모 방향으로 거슬러 올라가므로 최악의 경우 O(N)
  • 모든 쿼리 처리 시 O(NM)

최소 공통 조상 알고리즘 개선

• 메모리를 조금더 사용하여 각 노드에 대해 2^i번째 부모에 대한 정보 기록

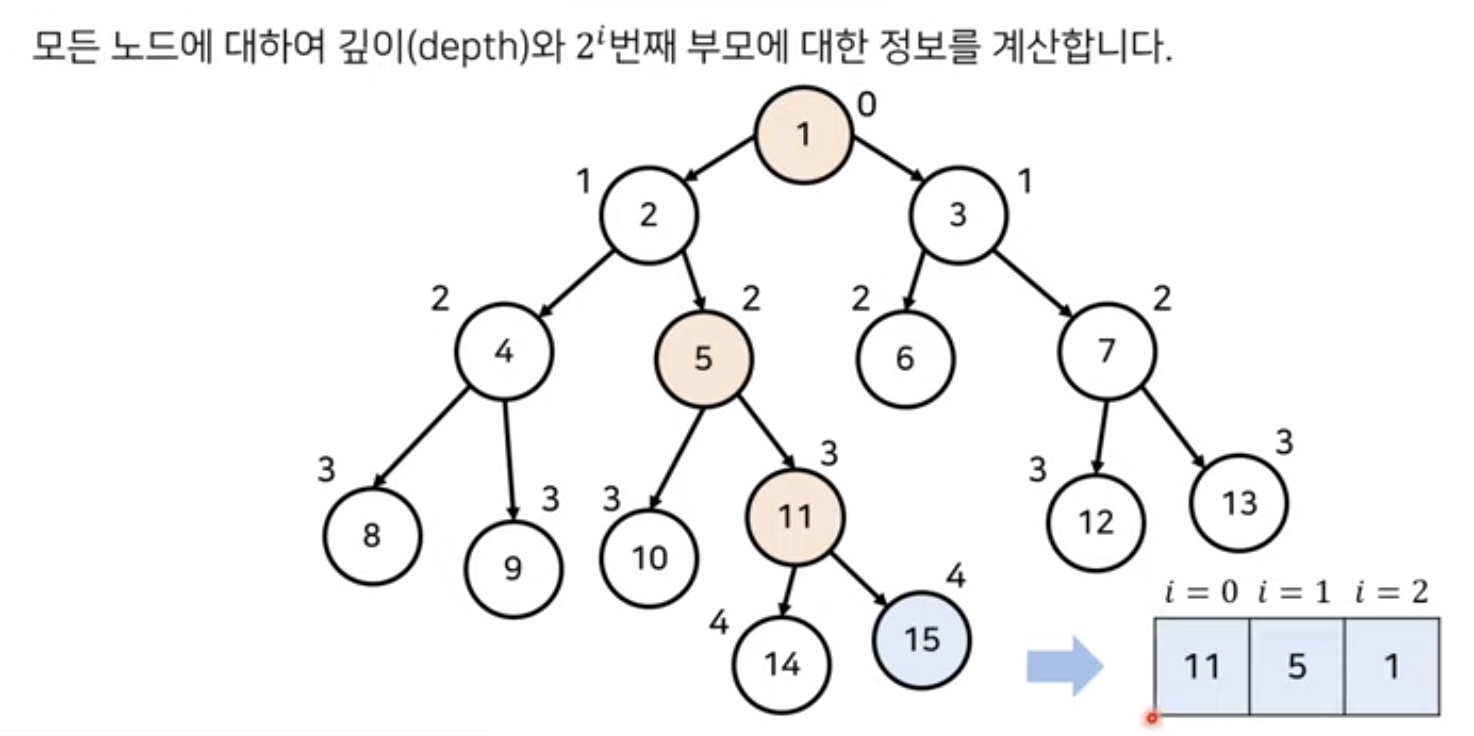
• 다이나믹 프로그래밍을 이오ㅛㅇ해 시간 복잡도 개선
• 매 쿼리마다 O(logN)
  • O(MlogN)

LO = 21
...

parent = [[0] * LOG for _ in range(n+1)]
...

def dfs(x, depth):
	c[x] = True
    d[x] = depth
    for y in graph[x]:
    	if c[y]:
        	continue
		parent[y][0] = x
		dfs(y, depth+1)

def set_parent():
	dfs(1, 0)
    for i in range(1, LOG):
    	for j in range(1, n+1):
        	parent[j][i] = parent[parent[j][i - 1]][i - 1]

def lca(a, b):
	if d[a] > d[b]:
    	a, b = b, a
	
    for i in range(LOG - 1, -1, -1):
    	if d[b] - d[a] >= (1 << i):
        	b = parent[b][i]
            
	if a == b:
    	return a
	for i in range(LOG - 1, -1, -1):
    	if parent[a][i] != parent[b][i];
        	a = parent[a][i]
            b = parent[b][i]
            
	return parent[a][0]
    
set_parent()

m = int(input())

for i in range(m):
	a, b = map(int, input().split())
    print(lca(a, b))