이것이 취업을 위한 코딩 테스트다 with 파이썬
1.Greedy

현재 상황에서 가장 좋아보이는 것만 선택하는 알고리즘그리디 알고리즘의 정당성을 고민하면서 문제 해결 방안을 떠올려야 한다.
2.Implementation

머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정 풀이는 쉽게 떠올리지만 소스코드로 옮기기 어려운 문제 시뮬레이션 완전 탐색 문제는 2차원 공간, 방향 벡터가 자주 활용된다.방향 벡터 : (dx, dy), (0, 1)동, (-1, 0)북, (0, -1)서, (1, 0)남
3.DFS & BFS

Search : 많은양의 데이터 중 원하는 데이터 찾는 과정반드시 숙지해야하는 유형First In Last OutFirst In First Out연산이 수학적으로 정의된 경우 코드가 더 간결해진다.두 개 자연수에 대한 최대 공약수를 구하는 대표적 알고리즘두 자연수 A,
4.Sort Algorithm

데이터를 특정 기준에 따라 순서대로 나열하는 것문제 상황에 따라 적절한 정렬 알고리즘이 공식처럼 사용된다.처리되지 않은 데이터 중 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸는 것을 반복선형 탐색 2중 반복문N번 만큼 가장 작은 수를 찾아 맨 앞으로 보내야
5.Binary Search Algorithm
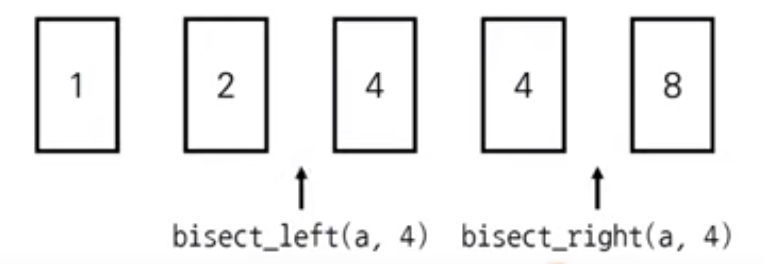
순차 탐색 : 데이터를 찾기위해 앞에서부터 데이터를 하나씩 확인이진 탐색 : 정렬되어있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정한다.단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는
6.Dynamic Programming
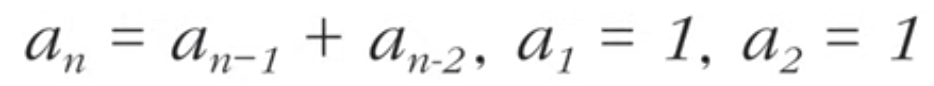
메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상 시키는 방법이미 계산된 작은 문제에 대한 결과는 별도 메모리 영역에 저장해 다시 계산하지 않는다.보통 선형 탐색문제를 이렇게 해결하면 비약적으로 시간 효율을 향상 시킬 수 있다.구현은 보통 탑다운, 바텀업으로
7.최단 경로
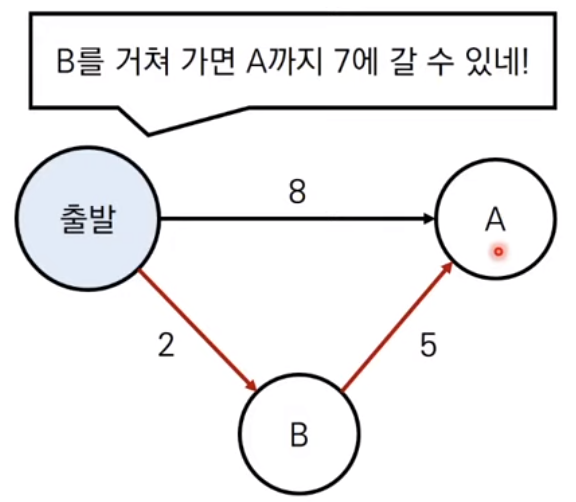
가장 짧은 경로 찾는 알고리즘다양한 상황한 지점에서 다른 한 지점까지의 최단 경로한 지점에서 다른 모든 지점까지의 최단 경로모든 지점에서 다른 모든 지점까지의 최단 경로그래프에서 노드로 표현, 연결된 것은 간선으로 표현특정 노드에서 출발하여 다른 모든 노드로 가는 최단
8.기타 그래프 이론
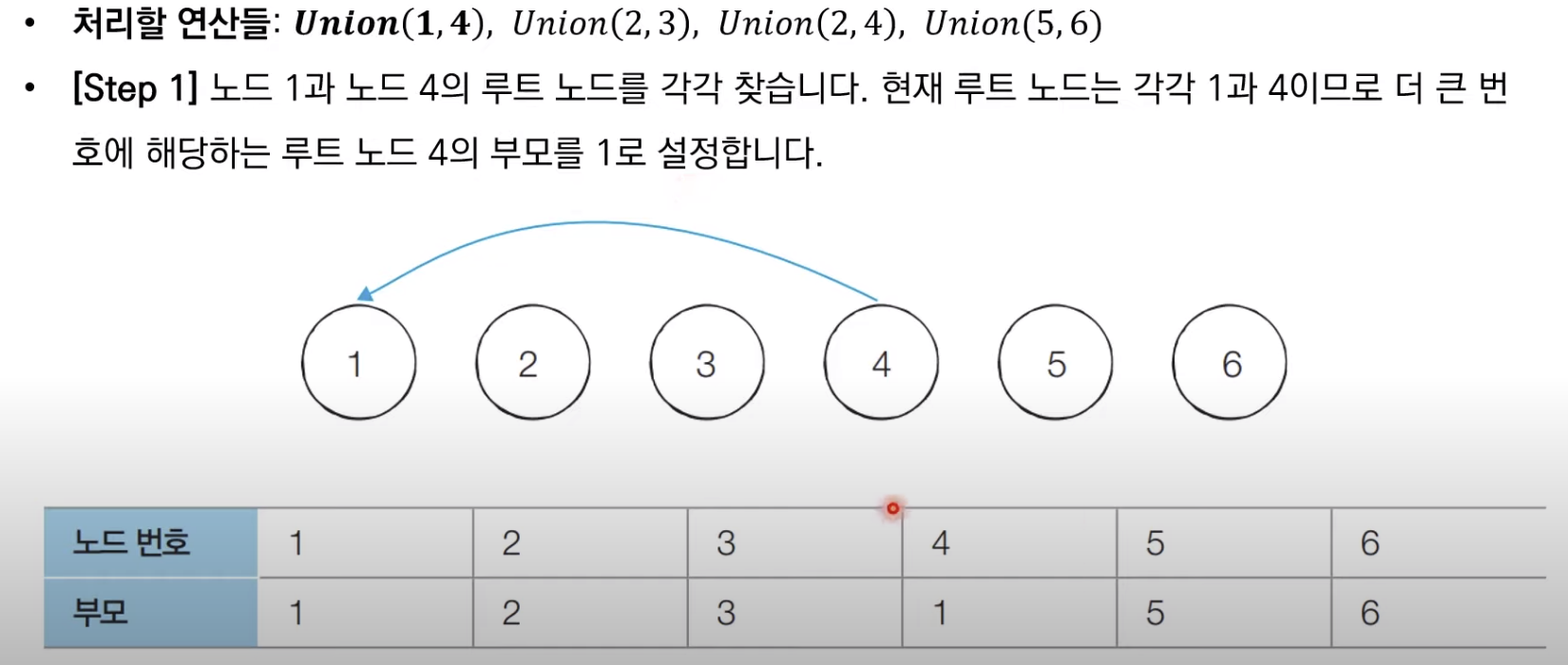
Disjoint Sets : 공통 원소가 없는 두 집합서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조두 종류의 연산 지원Union : 두 개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산Find : 특정 원소가 속한 집합이 어떤 집합인지 알
9.자주 출제되는 기타 알고리즘
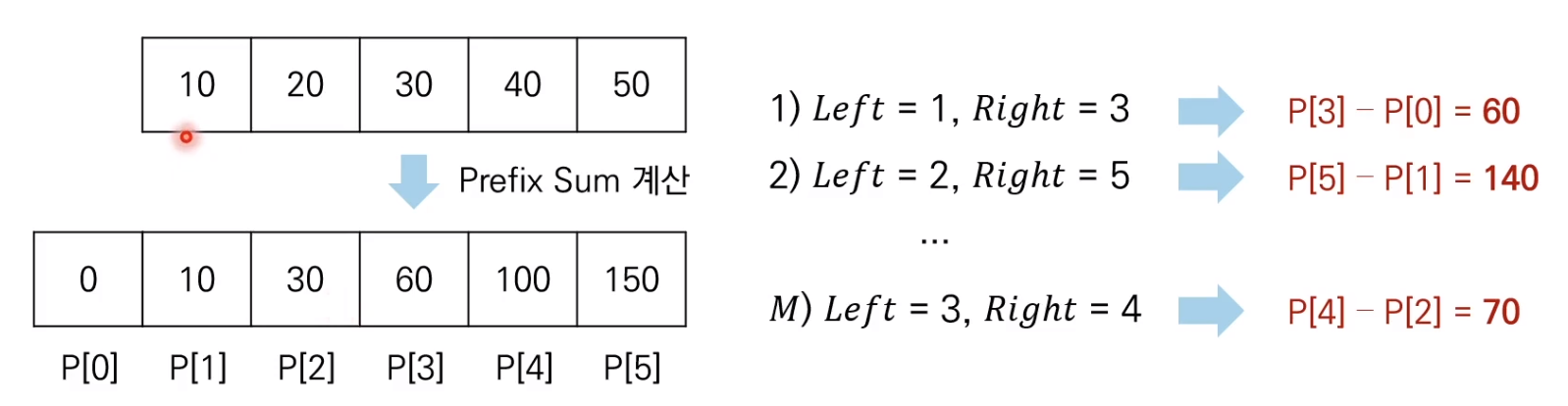
1보다 큰 자연수 중 1과 자기 자신을 제외한 자연수로는 나누어 떨어지지 않는 자연수2부터 X-1 까지 모든 자연수에 대해 연산 수행 => 시간 복잡도는 O(X)모든 약수가 가운데 약수를 기준으로 곱셈 연산에 대해 대칭을 이룬다.16의 약수 : 1, 2, 4, 8, 1
10.핵심 요약 시리즈
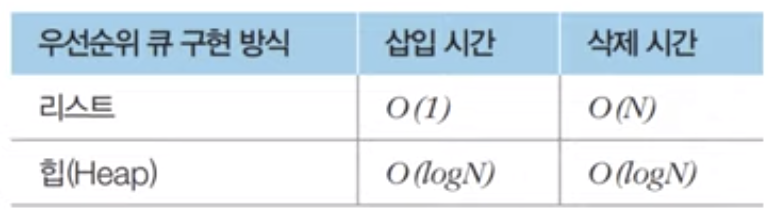
우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료 구조list와 prioirty queue의 시간 복잡도 비교 내용단순 N개 데이터를 힙에 넣었다가 꺼내는 작업은 정렬과 동일 (힙정렬)O(NlogN)완전 이진 트리 자료구조의 일종완전 이진 트리 : 루트 노드부터