Image Classification

Challenges

• Viewpoint variation
• Illumination
• Deformation
• Occlusion
• Background Clutter
• Intraclass variation

Data-Driven Approach 방법론

1. label이 있는 이미지 데이터들을 모은다.
2. 머신러닝을 이용해서 classifier를 train 한다.
3. 새로운 이미지를 대상으로 해당 classifier를 평가한다.

1. K-Nearest Neighbor

모든 train data들에 대하여 해당 데이터의 값들을 저장하고, test data와의 거리를 비교하여 가장 가까운 거리에 있는 label을 적용한다.

Hyperparameters of K-Nearest Neighbor

1. k (몇개의 점과 비교할 것인가)
   
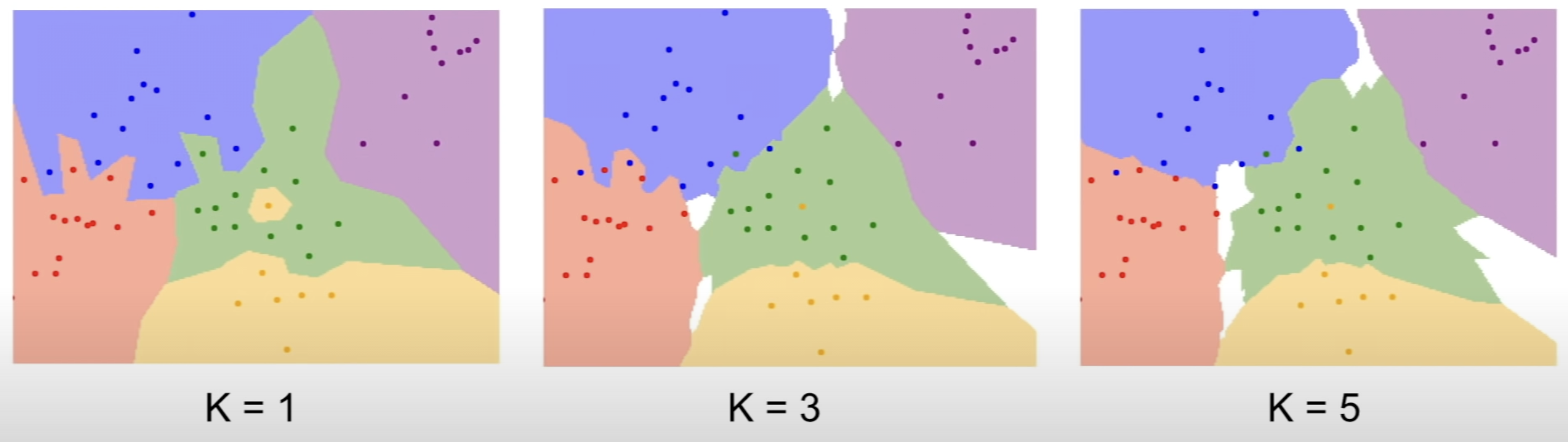
   출처 : cs231n Lecture2 | Image Classification

   그림에서 보듯이 k가 커지면 경계선이 평준화된다.

2. Distance Metirc

   두 점 $I_1, I_2$에 대하여, 거리를 비교하는 방법에는 두가지가 있다.

   • L1 Distance L1 distance는 차이의 절대값을 더해서 구한다.
     $d_1(I_1,I_2) = \sum_p|I_1^p - I_2^p|$
   • L2 Distance L2 distance는 차이의 제곱을 더한 후 해당 값을 제곱근 한 값을 이용한다.
     $d_1(I_1,I_2) = \sqrt{\sum_p(I_1^p - I_2^p)^2}$

Splitting Data

위와 같은 Hyperparameter들을 설정하기 위해서는

❗ **3단계가 필요하다.**

1. Train dataset으로 모델을 Train을 한다.
2. Validation dataset으로 Hyperparameter의 성능을 측정하고 최적의 Hyperparameter를 설정한다.
3. Test dataset으로 모델의 최종 성능을 확인한다.

이 3단계를 위해서는 data들을 3개로 분류할 필요가 있다.

그러므로 많은 상황에서 데이터들은 아래의 그림과 같이 분류된다.

출처 : cs231n Lecture2 | Image Classification

K-Nearest Neighbor의 한계점

하지만, K-Nearest Neighbor는 한계점이 있기 때문에 image에서는 잘 사용되지 않는다.

• 첫번째 한계점 데이터들 사이의 거리를 이용해서 test 이미지의 label을 예측하려면 해당 좌표계에 균등하게 데이터가 분포되어 있어야 된다. 이때, 데이터의 차원수가 커질수록 그것에 비례하여 많은 데이터들이 필요하기 때문에 rgb값을 이용하는 이미지에서는 사용하기에 한계가 크다.
  
• 두번째 한계점 데이터들과의 거리로 labeling을 하지만 그 거리들의 실질적인 의미가 없다.
  
• 세번째 한계점 모든 데이터들과 비교해야 되기 때문에 test time이 엄청나게 크다.
  

2. Linear Classification

Linear Classification은 $X$라는 이미지를 받았을때, $W$라는 weight와 $b$라는 bias를 이용해서 각 라벨별 확률을 구하게 된다.

이를 수식으로 표현하면

위와 같이 표현 할 수 있으며, 만약 이미지 x가 32323 사이즈로 구성되어있고, 3개의 카테고리로 분류 할 수 있으면,

W는 3 3072 행렬이고 x는 3072 1 행렬이며 b는 3 * 1 행렬이다.

위 수식을 그림으로 표현하면 아래와 같이 표현할 수 있다.

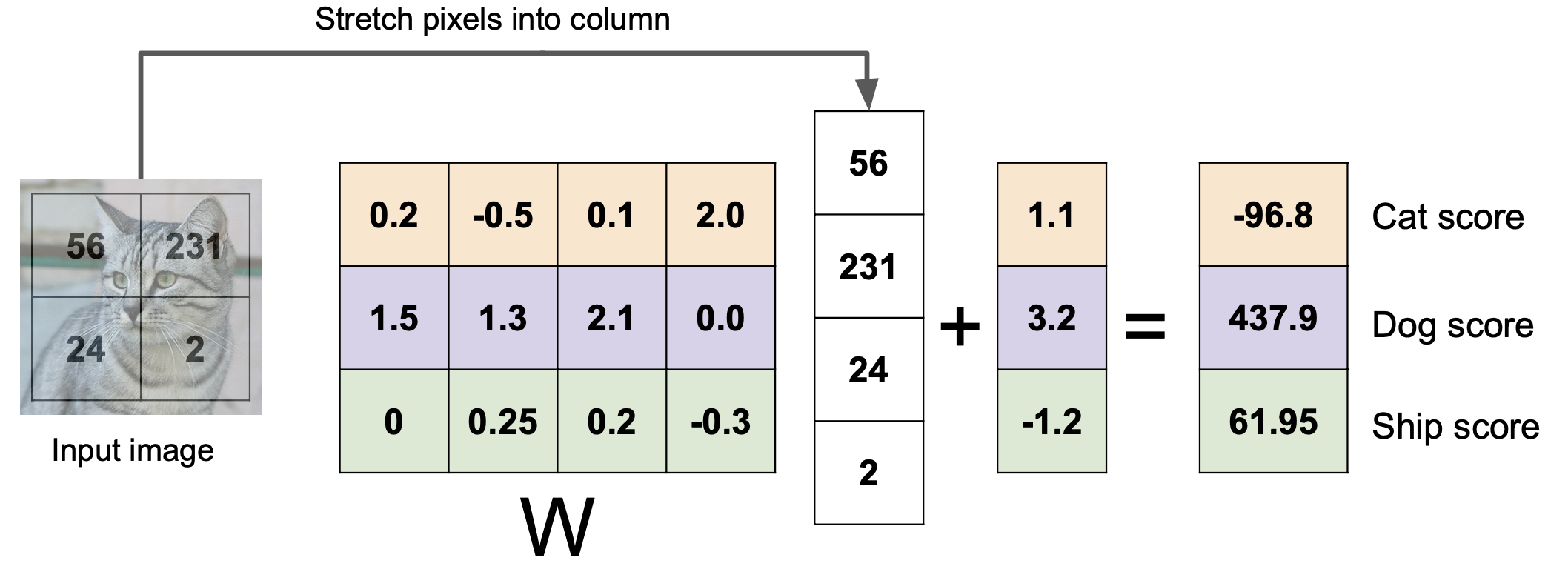
출처 : cs231n Lecture2 | Image Classification

이때, W 행렬의 row들은 각각의 label에 대한 템플릿이라고 생각 할 수 있으며, 해당 템플릿들에 대한 test 대상의 사진과의 유사도를 측정하는 방식이라고 이해 할 수 있다.

Linear Classification의 한계점

linear한 선으로 구분을 하는 방식으로 생각 할 수 있기 때문에 만약에 해당 label이 여러 군집으로 구성되어 있는 경우, 해당 label을 구분하기에는 힘들 수 있다.