Disjoint Set

용어

• Set은 개체들의 집합 (리스트 등과 달리 순서는 고려하지 않음)

• Set A의 모든 원소가 셋 B에 포함될 때 A를 B의 부분집합(subset)이라한다. 이 때 B는 A의 초월집합(superset)이라 한다.

• Set A와 셋 B가 공유하는 원소가 하나도 없을 때 A와 B를 mutually disjoint하다고 한다.

• 임의의 셋을 분할(partition)한다는 건 각 부분집합이 다음 두 가지 속성을 만족하는 Disjoint Set이 되도록 셋을 쪼개는 걸 뜻한다.

  1) 파티션된 부분집합을 합치면 원래의 셋이 된다.
  2) 파티션된 부분집합끼리는 mutually disjoint, 즉 겹치는 원소가 없다.

결론

Disjoint Set = 서로 중복되지 않는 부분 집합들 로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
즉, 공통 원소가 없는, 즉 “상호 배타적” 인 부분 집합들로 나눠진 원소들에 대한 자료구조이다.(서로소 집합)

---

Union Find

개념

• Disjoint Set을 표현할 때 사용하는 알고리즘

집합을 구현하는 데는 비트 벡터, 배열, 연결 리스트를 이용할 수 있으나 그 중 가장 효율적인 트리 구조를 이용하여 구현한다.
세 가지 연산을 이용하여 구현한다.

연산

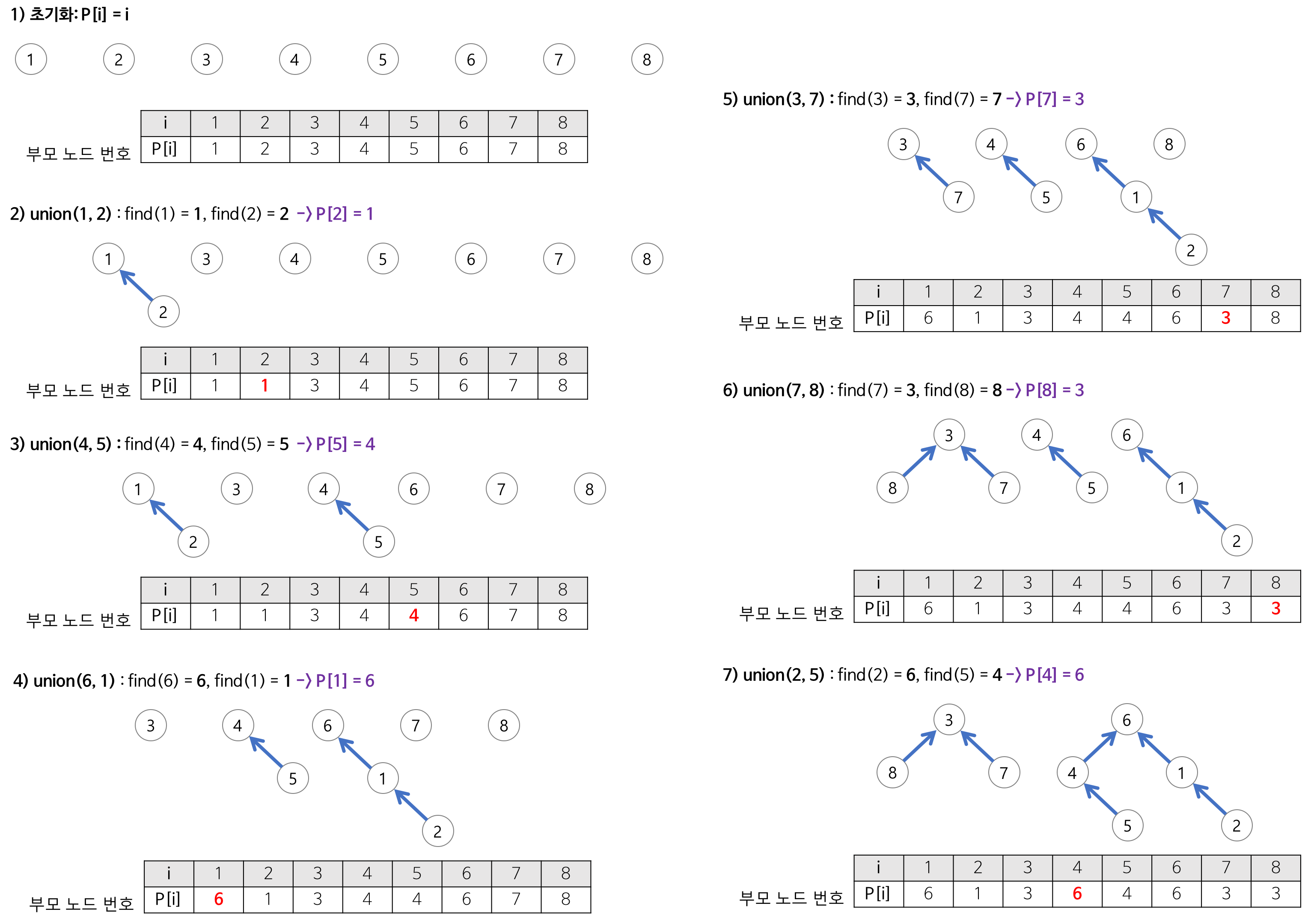
• make(x)
  • 초기화
  • 처음에 각각의 원소들은 연결된 정보가 없기 때문에 부모로 자기 자신을 가지게 한다.
• union(x,y)
  • 합하기
  • x가 속한 집합과 y가 속한 집합을 합친다. 즉, x와 y가 속한 두 집합을 합치는 연산
  • x와 y의 부모를 하나로 통일
• find(x)
  • 찾기
  • x가 속한 집합의 대표값(부모)을 반환한다. 즉, x가 어떤 집합에 속해 있는지 찾는 연산

Union Find의 과정

Union Find 사용처

집합에서 구성 요소가 겹치지 않게 분할할때 사용(서로소인지 판별)

대표

• Kruskal MST 알고리즘에서 새로 추가할 간선의 양끝 정점이 같은 집합에 속해 있는지(사이클 형성 여부 확인)에 대해 검사

구현-JAVA

public class Union_Find {
    static int arr[];
    public void union(int a,int b) {
        a = find(a);
        b = find(b);
        arr[b]=a   
    }
    public int find(int a) {
        if(arr[a]==a)
            return a;
        else
            return find(a);
    }

}

Union-Find 개선점

최악의 상황

• 트리 구조가 완전 비대칭인 경우

  연결 리스트 형태
  트리의 높이가 최대가 된다.
  원소의 개수가 N일 때, 트리의 높이가 N-1이므로 union과 find(x)의 시간 복잡도가 모두 O(N)이 된다.
  배열로 구현하는 것보다 비효율적이다.

Find 최적화

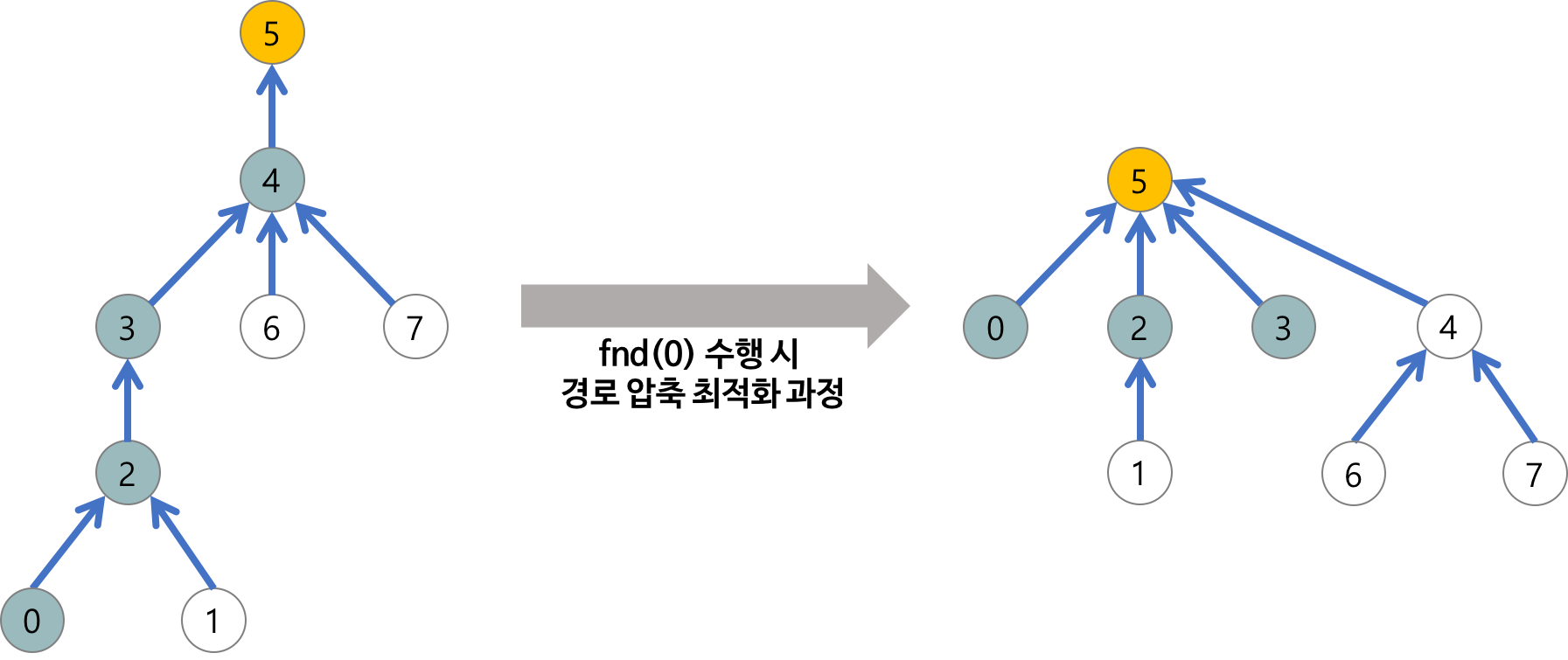
• 경로 압축

• 시간 복잡도: O(logN)

  
    public int find(int a) {
        if(arr[a]==a)
            return a;
        else
            return arr[a] = find(a);
    }

Union 연산 최적화

• union-by-rank(union-by-height)
• rank에 트리의 높이를 저장한다.
• 항상 높이가 더 낮은 트리를 높은 트리 밑에 넣는다.

    static int rank[]; //arr사이즈와 동일
    public void union(int a,int b) {
        a = find(a);
        b = find(b);
        if(a == b)
             return;
        if(rank[a] < rank[b]) {
             arr[a] = b; // x의 root를 y로 변경
           } else {
             arr[b] = a; // y의 root를 x로 변경
             if(rank[a] == rank[b])
                   rank[a]++;
        }
    }