다이나믹 프로그래밍

정의

특정 범위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘 설계 기법
'하나의 문제는 단 한 번만 풀도록 하는 알고리즘'

대상

• 최적 부분 구조(Optimal substructure)
  기본 문제의 최적해가 부분 문제의 최적해를 포함하고 있을 때, 그 문제는 최적 부분 구조를 가진다.
• 분할 정복 기법
  동일한 문제를 다시 푼다 ex) 피보나치 재귀

예시 - 피보나치

단순 분할 정복 피보나치

• 피보나치 수열의 점화식: D[i] = D[i - 1] + D[i - 2]
  
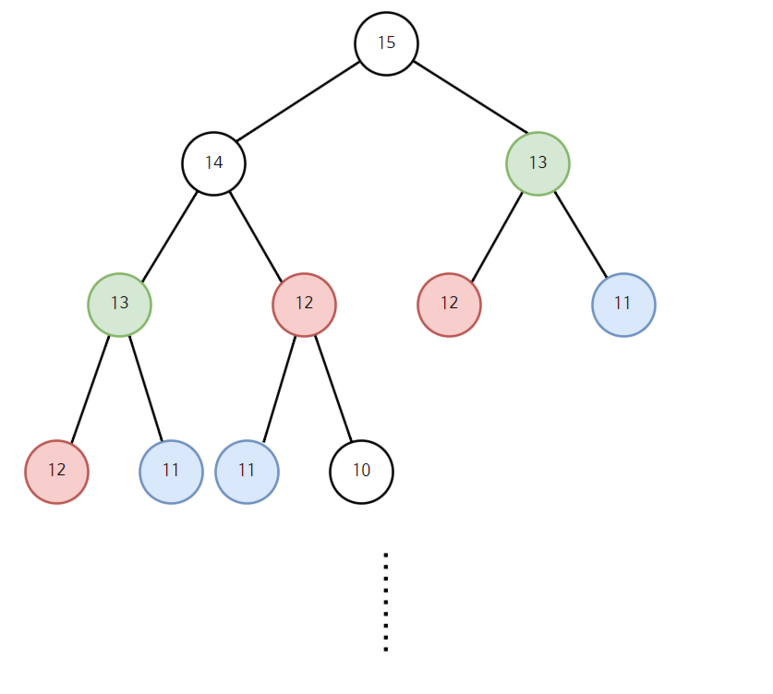
  위의 그림에서는 13, 12, 11과 같은 경우를 여러번 반복하여 풀게 된다.
  이러한 단순 피보나치를 코드로 표현하면 다음과 같다.

	public int fibonacci(int x){
        if(x==1)
            return 1;
        if(x==2)
            return 2;
        return fibonacci(x-1)+fibonacci(x-2);
        }

이미 구한 값을 또 연산하기에 굉장히 비효율적이다.
이를 해결하기 위해서는 Top-Down & Bottom-up 방식이 존재한다.
두 방식은 알고리즘 뿐만 아니라 소프트웨어 설계 등 다방면에서 사용되는 이론이지만, 현재는 알고리즘에 대해서만 작성해보도록 하겠다.

Top-Down 방식

큰 문제를 풀어 해결되지 않았다면 작은 부분을 호출하여 문제를 해결하는 방식

• 장/단점
  설계에서의 장단점과 동일하다.

  • 장점 : 설계가 쉽다. 재귀로 작성하는 코드라 보기 쉽고 따라서 함수의 점화식을 이해하기 쉽다.

  • 단점 : 재귀함수이기 때문에 퍼포먼스가 좋지 않을 수 있다. 재귀함수의 스택이 너무 많이 쌓이면 문제가 생긴다.

    (설계에서의 시작이 간단하지만 저수준에서의 복잡성이 최상위 수준에 영향을 미치게 되어 필요 이상으로 복잡해지는 문제점과 동일)

• 구현방법 : 각 구현에 중복된 값을 memoization 기법을 통해 처리하여 중복된 연산을 하지 않게 한다.

  • 메모이제이션?

    이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거

• 코드 - 피보나치

	static int memoization[];
    public int fibonacci(int x){
        if(x==1)
            return 1;
        if(x==2)
            return 2;
        if(memoization[x]!=0) return memoization[x];
        memoization[x] = fibonacci(x-1)+fibonacci(x-2);
        return memoization[x];
    }

Bottom-UP 방식

가장 작은 부분의 문제들 부터 해결하며 전체 문제를 해결하는 방식

Tabulation : 작은 문제들의 결과부터 테이블을 채워나가는 방식

• 장/단점

  • 장점 : 재귀 호출로 인한 퍼포먼스 저하, 메모이제이션을 통한 메모리 소모가 없다.

  • 단점 : 대부분의 사람들은 큰 개념으로 작은 개념을 만드는 것을 더 잘한다. -> 어렵다.

    ex) 레고를 조립할 때 항상 다 조립했는데 레고가 남는 문제

• 구현방법

  • 반복해야 할 작은 점화식을 찾아내서 반복문으로 구현한다.
  • 대부분의 알고리즘 문제를 풀 때 배열을 하나 만들어서 차곡차곡 쌓아가는 형태를 사용한다.

• 코드 - 피보나치

      static int dp[];
      public int fibonacci(int x){
          dp[0] = 0;
          dp[1] = 1;
          for (int i = 2; i <= x; i++)
              dp[i] = dp[i - 1] + dp[i - 2];
          return dp[x];
      }