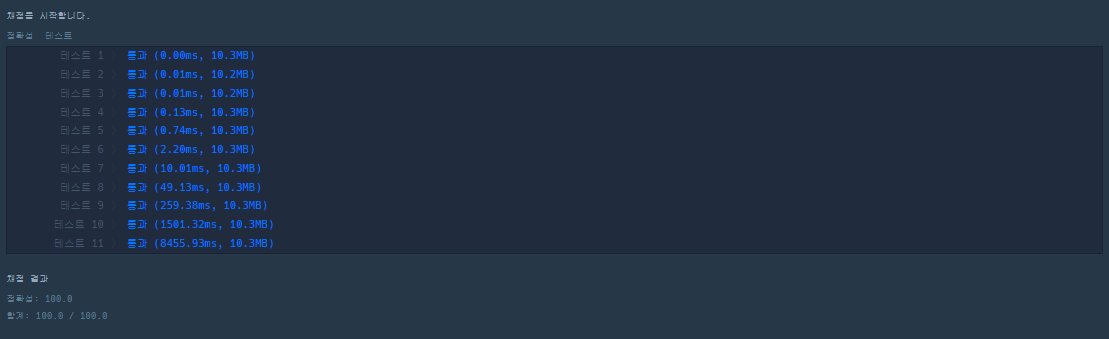
[출처] : https://programmers.co.kr/
문제
가로, 세로 길이가 n인 정사각형으로된 체스판이 있습니다. 체스판 위의 n개의 퀸이 서로를 공격할 수 없도록 배치하고 싶습니다.
예를 들어서 n이 4인경우 다음과 같이 퀸을 배치하면 n개의 퀸은 서로를 한번에 공격 할 수 없습니다.

체스판의 가로 세로의 세로의 길이 n이 매개변수로 주어질 때, n개의 퀸이 조건에 만족 하도록 배치할 수 있는 방법의 수를 return하는 solution함수를 완성해주세요.
제한사항
- 퀸(Queen)은 가로, 세로, 대각선으로 이동할 수 있습니다.
- n은 12이하의 자연수 입니다.
입출력 예
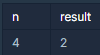
풀이
백트래킹 문제의 대표적인 예시이다.
백트래킹은 모든경우의 수를 탐색하는 과정에서 해답이 되지 않을것이라고 판단되면 그 즉시 해당 경우를 버리고 뒤로 돌아와서 다른 경우부터 탐색하는 전략이다.
보통 DFS로 구현을 하고 트리에서 해답이 될 가능성이 보이지 않으면 해당 가지를 처내고 부모노드로 와서 다른 노드부터 다시 탐색을 하게 된다.
문제로 돌아와서 N-Queen의 경우, 퀸을 특정위치에서 두었을때 나올수 있는 경우의 수를 전부 트리에 넣고 탐색을 하는 것이다.
이때 답이 될 가능성이 없다면 부모로 돌아와서 다른 경우를 따지게 된다.
아래의 그림은 N-Queen의 경우를 트리로 나타낸 예시이다.
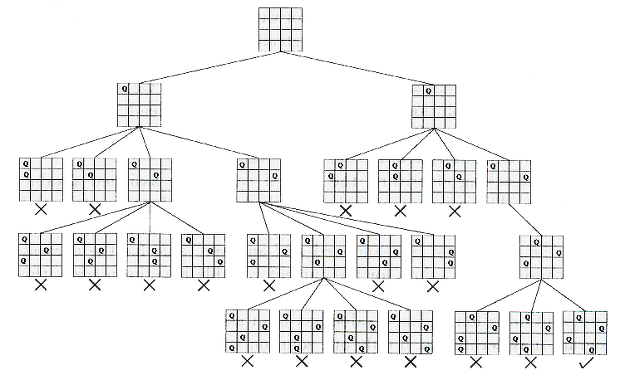
위의 그림처럼 체스판이 주어지고 첫번째줄부터 퀸을 놓고, 그로부터 파생되면 경우를 트리를 그려가며 찾게 된다.
다음 퀸을 두었을 때 조건에 해당하지 않으면 더 이상 해당경우는 탐색할 필요가 없어지기 때문에 더 볼것도 없이 부모로 이동해서 다른 경우를 탐색하여 경우의 수를 줄여가며 탐색하는 것이다.
이 문제의 접근은 위의 그림처럼 접근했다.
우선 퀸의 위치좌표를 담고 있을 리스트를 만들었다.
이를 1차원 리스트로 만들어서 인덱스가 column, 리스트의 값이 row가 된다
예를 들면 [1,2,3,4] => (0,1),(1,2),(2,3),(3,4) 이다
2차원 배열이 아닌 1차원으로 표시한 이유는 어차피 각 row에는 하나의 퀸만 위치 할수 있기 때문에 불필요하게 2차원 배열을 사용할 필요가 없어서 였다.
그 다음으로 bfs함수와 check 함수를 만들어준다.
bfs함수는 재귀적으로 트리를 탐색하게 될 함수이고, check 함수는 각 경우마다 조건에 부합하는지를 확인하는 함수이다.
check 함수는 퀸의 위치가 담긴 정보를 리스트로 받고, 가장 최근에 추가한 퀸의 위치중 row값을 인자로 받는다.
이 값들을 받아서 0번째 row(체스판에서 가장 윗줄)부터 인자로 받은 row값까지 탐색을 진행한다.
반복문을 이용해서 0부터 row 까지 하나씩 증가시켜가면서 인자로 받은 퀸의 위치정보가 담긴 queen 리스트에 인덱스로 값을 조회한다.
만약 이 값이 인자로 받은 row값을 인덱스로 조회한 값과 같다면(queen[i] == queen[row]) 동일한 column상에 있는 것이다.
그 다음으로 대각선을 확인한다.
대각선은 두 위치(queen[i] queen[row]) 세로길이(abs(queen[row]-queen[i]))와 가로길이(row-i)를 비교한다
이 두값이 같다면 서로 대각선에 위치한것이다.
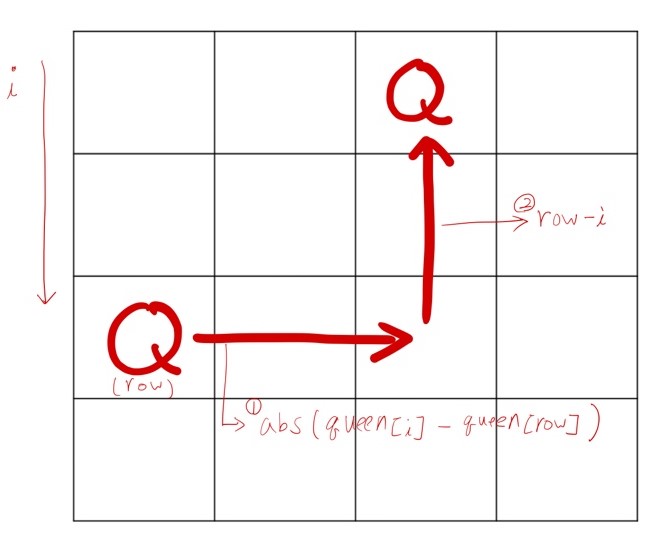
(조금이라도 이해가 잘 되었으면 해서 그림을 그려봤다.)
위의 그림처럼 i는 0부터 row의 위치까지 하나씩 탐색을 하게 된다.
그림의 ①==②이 같다면 같은 대각선에 놓이게 된다.
check를 통해서 조건에 부합하는 것을 확인하면 재귀함수의 row인자에 +1을 해서 다음 경우를 반복적으로 탐색하게 한다.
아래 코드에 주석을 달아놨으니 한번 읽어보면 이해하는데 도움이 될것이다.
#현재상태가 조건을 만족하는지(퀸이 서로 공격을 할수 없는지) 체크하는 함수
#False면 조건을 만족하지 않음
def check(queen:list,row:int)->bool:
#주어진 row => 좌표상 맨위(row가 0) 부터 하나씩 차근차근 채워내려가기 때문에 주어진 row를 인덱스로 하는 queen의 값이 최근에 추가된 퀸의 위치
#따라서 0부터 해당 row까지 비교하면서 서로 공격할수 있는 위치인지 확인
#퀸은 가로세로 대각선으로 이동이 가능하다.
for i in range(row):
#queen리스트에서 i번째와 row번째가 같으면 동일 컬럼에 있기 떄문에 퀸이 서로 공격가능, 즉 놓을수 없음
#row-i => 두 좌표의 세로로 떨어진 정도 , queen[row] - queen[i] => 두 좌표의 가로로 떨어진 정도
#위의 두 값이 같으면 같은 대각선상에 있음, 예를 들면 (1,1) (3,3)은 가로,세로가 각각 2씩 떨어져 있다. 즉 같은 대각선 상에 있음
#row-i=> 이경우는 항상 row가 크거나 i와 같기 때문에 그대로 빼면되지만, queen[row] - queen[i] 이 경우는 row인덱스의 위치가 더 왼쪽에 있으면 음수가 나옴
#따라서 절댓값을 취해줌
if queen[i] == queen[row] or abs(queen[row]-queen[i]) == row-i:
return False
return True
#재귀함수 - 각 경우에 대해서 탐색하는 함수
def bfs(queen:list,row:int) -> int:
length = len(queen)
#배치할 퀸의 개수 카운트
count = 0
#계속탐색하다 탐색하는 row가 좌표평면의 끝에 도달하면 종료
if length == row:
return 1
#좌표평면의 끝이 아니면 row+1 해서 자기 자신호출에서 탐색을 계속 함
for i in range(length):
#퀸을 주어진 row에서 컬럼을 바꿔가면서 넣어봄
queen[row] = i
#퀸을 넣어보고 check함수를 돌려서 조건에 맞게 퀸이 안겹치는지 확인
if check(queen,row):
#조거네 맞으면 row를 하나 증가시켜서 반복하고 발새한 count값을 계속 더함
count+=bfs(queen,row+1)
return count
def solution(n:int)->int:
#퀸의 위치를 담을 리스트 - 같은 row에는 하나의 퀸밖에 올수 없어서 인덱스를 row로 함,
#예를들어 [1,2,3,4]이면 (0,1),(1,2),(2,3),(3,4) => 같은 row에는 어차피 퀸이 하나 밖에 오지못함
queen_location = [0]*n
#0번째 row부터 시작하기 떄문에 row 위치에 0을 넣음
answer = bfs(queen=queen_location,row=0)
return answer결과
백트래킹으로 경우의 수를 줄이지 않고 dfs로 완전탐색을 했다면 시간초과가 났을것이다.