[출처] : https://programmers.co.kr/
문제
회사원 Demi는 가끔은 야근을 하는데요, 야근을 하면 야근 피로도가 쌓입니다. 야근 피로도는 야근을 시작한 시점에서 남은 일의 작업량을 제곱하여 더한 값입니다. Demi는 N시간 동안 야근 피로도를 최소화하도록 일할 겁니다.Demi가 1시간 동안 작업량 1만큼을 처리할 수 있다고 할 때, 퇴근까지 남은 N 시간과 각 일에 대한 작업량 works에 대해 야근 피로도를 최소화한 값을 리턴하는 함수 solution을 완성해주세요.
제한사항
- works는 길이 1 이상, 20,000 이하인 배열입니다.
- works의 원소는 50000 이하인 자연수입니다.
- n은 1,000,000 이하인 자연수입니다.
입출력 예 설명
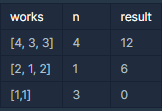
입출력 예 #1
n=4 일 때, 남은 일의 작업량이 [4, 3, 3] 이라면 야근 지수를 최소화하기 위해 4시간동안 일을 한 결과는 [2, 2, 2]입니다. 이 때 야근 지수는 22 + 22 + 22 = 12 입니다.
입출력 예 #2
n=1일 때, 남은 일의 작업량이 [2,1,2]라면 야근 지수를 최소화하기 위해 1시간동안 일을 한 결과는 [1,1,2]입니다. 야근지수는 12 + 12 + 22 = 6입니다.
접근(1)
이 문제는 제곱의 합을 최소화 하는 문제였다.
제곱의 합이 최초가 되려면 모든 값의 편차가 최소가 되어야 한다.
남은 일의 작업량이 [4,3,3],[5,2,3],[5,1,4]인것들로 예를 들어보겠다
각각의 제곱의 합은 34,38,41이다
이를 보면 각 값들의 차이가 작은 [4,3,3]이 작은 것을 볼수가 있다.
따라서 야근지수를 최소화 하기 위해서는 남은 일의 작업량들의 차이가 최소가 되게 만들어 주어야 한다.
아래 코드를 보게 되면, 우선 남은 일의 총량이 퇴근시간보다 작으면 계산할 필요 없이 0을 반환하도록 했다.
남은 일의 총량이 퇴근시간보다 많으면 반복문을 돌면서, 매 반복마다 남은 일의 작업량(works)중에서 가장 큰수를 골라서 남은 시간인 n이 0이 될때까지 -1을 해준다.
그렇게 되면 각각의 남은 일의 작업량들의 크기가 비슷해지게 되어 야근지수를 계산하면 최소가 되게 된다.
이를 구현하기 위해서 max함수를 이용해서 가장 큰수를 선택했는데 max 함수의 시간복잡도가 O(N)이다 보니 효율성에서 시간초과가 걸리게 되었다.
def solution(n, works):
answer = 0
total_works = sum(works)
#남은 일의 총량이 퇴근시간보다 작으면 0
if total_works <= n:
return 0
#남은 시간만큼 works 중에 최대값을 찾아서 -1 씩함(남은 시간을 다 쓸때까지)
for _ in range(n):
#최대값이 있는 인덱스를 찾아서 빼줌
works[works.index(max(works))] -= 1
for i in works:
answer += i*i
return answer접근(2)
max함수를 이용한 접근은 시간초과로 인해서 효율성을 통과하지 못했다
max함수의 시간복잡도가 O(n)이므로 이를 좀 더 줄일수 있는 자료구조인 heap구조를 이용해서 시간복잡도를 좀더 줄여보았다(힙은 O(logn)이다)
힙을 구현하기 위해서 파이썬의 heapq라이브러리를 사용했는데, heapq라이브러리의 경우 루트에 최소값이 오는 minheap이다
문제에서 원하는 것은 최대 값이므로 maxheap을 구현하기 위해서 heap에 넣을 값에 -1을 곱해서 넣어주고 pop한 후에 다시 -1을 곱해주면 maxheap처럼 사용할수 있다.
def solution(n, works):
answer = 0
#남은 일의 총량이 퇴근시간보다 작으면 0
if sum(works) <= n:
return 0
#힙 자료구조
queue = list()
#works를 heap에 넣어줌 -> max으로 동작시키기 위해서 -1을 곱해서 넣음
for i in works:
heapq.heappush(queue,i*(-1))
#works를 균등하게 나누기 위해서 반복문을 돌면서 가장 큰값 -1을함
for _ in range(n):
#힙에서 뻄
temp = heapq.heappop(queue)
#뺀값에 +1을해서(원래-1인데 최대힙으로 만들기 위해서 -1을 곱해줬으니 +1을 해줌)
#+1을 하고 다시 힙에 넣음
heapq.heappush(queue,temp+1)
#최종적으로 나열된 값들을 야근지수공식에 맞게 계산함
for i in queue:
answer += i*i
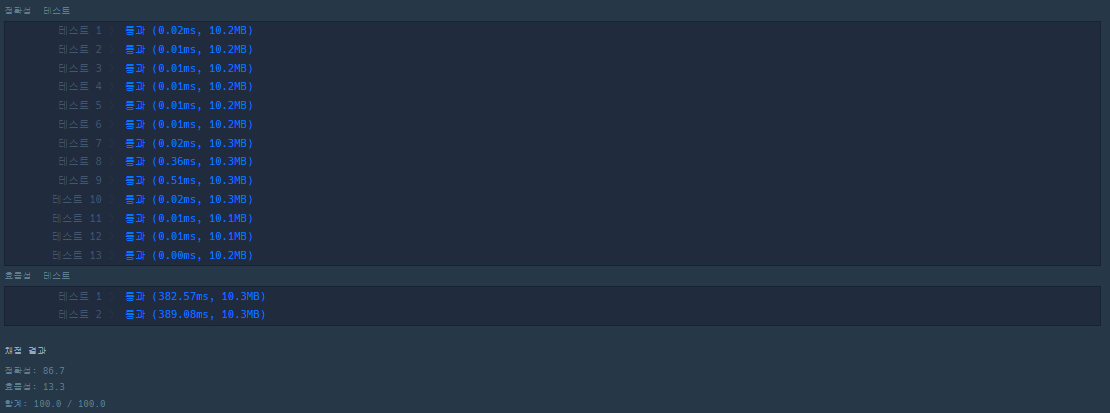
return answer결과
힙으로 구현을 하니 효율성을 통과하는 모습을 볼수 있다.