[프로그래머스 - Level 3] 정수 삼각형

lsh9672·2022년 2월 4일

programmers

목록 보기

10/13

문제

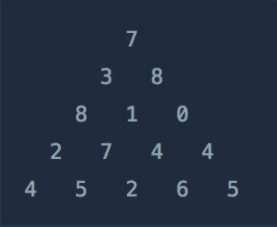
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

제한사항

삼각형의 높이는 1 이상 500 이하입니다.
삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.

입출력 예

접근(1)

삼각형의 맨위에서 부터 아래로 내려갈수 있는 경로중에 가장 값이 큰 경우를 찾는 문제이다
아래로 내려갈때는 대각선방향으로 왼쪽또는 오른쪽으로 한칸만 이동할수 있다.

이 문제는 다음과 같은 순서로 접근했다.

1. 맨위에서 부터 아래로 더해나감
2. 더한값을 그대로 저장함
3. 더할떄는 옆의 값이 더해졌을때 더 클수도 있으니 비교함
4. 가장 마지막줄에 최종적으로 더해진 값들이 있고, 그중에서 가장 큰 값 선택

우선 삼각형이 2차원배열로 주어지기 때문에 왼쪽 대각선 이동은 배열에서 보면 바로 아래로 한칸이동하는 것으로 생각했다.

처음으로 삼각형의 높이가 1이라면 숫자가 하나 있는 것이므로 그대로 1개있는 수를 출력하도록 했다.

만약 2이상이라면 삼각형의 제일 맨위부터 한줄씩 내려가면서 숫자를 더해나갔다.

각값들은 왼쪽대각선아래 오른쪽 대각선아래에 더하게 되는데, check변수를 두어서 True이면 왼쪽대각선아래에 값을 더하고 False 이면 더하지 안도록 했다
이는 바로전에 있는 값이 더 커서 이 값을 오른쪽아래에 더했으면 그 다음 값은 왼쪽에 더할필요가 없기 때문이다

간단한 예를 들어보겠다.

8 3
8 1 0

다음과 같은 경우에서 반복문의 위치가 8,3에 위치했다고 가정하겠다.
처음 8을 오른쪽 대각선에 더하면 9가 되고, 다음 수인 3을 왼쪽대각선에 더한수는 4가 된다.
즉, 8일때가 더 크기 때문에 8이 오른쪽 대각선에 더해지면, 3은 왼쪽대각선에 더할필요가 없다.

이를 8부분에서 계산시에 바로 옆의 값인 3과 비교를 해서 check 변수를 False로 바꿔주면, 3은 왼쪽대각선에 덧셈을 하지 않게 된다.

이 과정을 반복하면서 마지막 열에 최종값이 더해지고 이중 가장 큰것을 선택해주면 된다.

def solution(triangle:list) -> int:
    
    #삼각형의 높이가 1이면 그대로 출력
    if len(triangle) == 1:
        return triangle[0][0]


    #첫번째 줄 부터 순차적으로 내려가면서 탐색
    for i in range(len(triangle)-1):
        
        #check변수가 True이면 왼쪽에 값을 더하고
        #False이면 왼쪽에 값을 더하지 않음
        #이것을 사용한 이유는 현재 값에서 다음 줄의 오른쪽에 더했을떄 값이 다음 값에서 다음줄의 왼쪽에 더했을떄 값보다 크다면 
        #다음 값은 왼쪽에 더할필요가 없기 때문이다.
        check = True
        #한줄에 있는 값들을 꺼내서 다음 값들에 더함
        for j in range(len(triangle[i])):

            #왼쪽, 즉 인덱스상으로 바로 아래에 더하는 값(+1,0)
            if check == True:
                triangle[i+1][j] += triangle[i][j]

            '''
            오른쪽대각선에 더하는 값(인덱스로 따지면 (+1,+1))
            이경우에는 옆에 있는 값과 비교해야됨
            옆(컬럼+1)에 있는 값이 더 크면 그냥 패스함
            인덱스의 끝이면 멈춤
            '''
            
            #마지막 값이면 그냥 오른쪽에 더하고 아래 연산 실행안하도록 패스
            if j == len(triangle[i])-1:
                triangle[i+1][j+1] += triangle[i][j]
                break

            #오른쪽아래에 더했을때
            temp_right_value = triangle[i+1][j+1] +triangle[i][j]

            #오른쪽값이 왼쪽아래에 더했을때
            temp_next_left_value = triangle[i+1][j+1] + triangle[i][j+1]

            #두 값중에 오른쪽아래에 더한값이 더 크면 check를 False로 만들어서 다음 연산에서 왼쪽에 안더하도록함
            if temp_right_value >= temp_next_left_value:
                triangle[i+1][j+1] = temp_right_value
                check = False

            else:
                check = True

    #제일 마지막줄에 최종적인 숫자의 합이 저장됨
    #이를 정렬하고 제일 뒤의 값 출력(가장 큰수이므로)
    #max를 쓰지 않는 이유는 시간복잡도가 O(n)이고 정렬은 O(nlogn)이다

    result = sorted(triangle[-1])
    
    return result[-1]

접근(2)

위의 풀이가 좀 지저분해서 다른 풀이도 생각해보았다.
원리는 동일하다
다른점은 3가지 경우로 나눠서 계산하게 했다.
왼쪽 끝에 있다면 왼쪽아래(배열에서 바로 아래)에 더하고, 오른쪽 값과 비교해서 오른쪽 아래 대각선에 더하도록 했다.

오른쪽 끝이라면 오른쪽 대각선 아래에만 더하도록 했다.
이경우는 전의 값에서 비교해서 왼쪽아래는 이미 연산이 끝났기 때문이다.

마지막 경우는 둘다 아닐때이고 이경우는 다음값과 비교해서 오른쪽 아래 대각선에 더하도록 했다.

코드를 보면 바로 이해가 될것이다.

def solution2(triangle:list) -> int:

        #삼각형의 높이가 1이면 그대로 출력
    if len(triangle) == 1:
        return triangle[0][0]

    #첫번째값은 미리 업데이트
    triangle[1][0] += triangle[0][0]
    triangle[1][1] += triangle[0][0]

    for i in range(1,len(triangle)-1):

        for j in range(len(triangle[i])):

            #왼쪽 끝일때
            if j==0:
                triangle[i+1][0] += triangle[i][0]
                triangle[i+1][1] += max(triangle[i][0],triangle[i][1])

            #오른쪽 끝일때
            elif j==(len(triangle[i])-1):
                triangle[i+1][-1] += triangle[i][-1]

            #둘다 아닐때 - 다음값과 비교해서 더큰값을 더함.
            else:
                triangle[i+1][j+1] += max(triangle[i][j],triangle[i][j+1])

    result = sorted(triangle[-1])
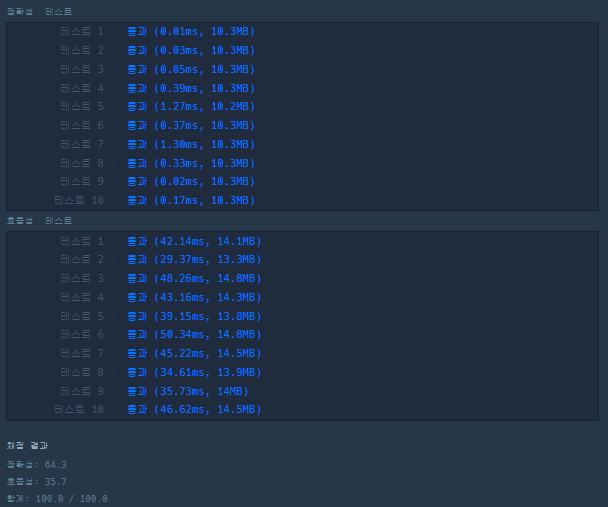
    return result[-1]