문제

프렌즈 블록이라는 신규 게임이 출시되었고, 어마어마한 상금이 걸린 이벤트 대회가 개최 되었다.

이 대회는 사람을 대신해서 플레이할 프로그램으로 참가해도 된다는 규정이 있어서, 게임 실력이 형편없는 프로도는 프로그램을 만들어서 참가하기로 결심하고 개발을 시작하였다.

프로도가 우승할 수 있도록 도와서 빠르고 정확한 프로그램을 작성해 보자.

게임규칙
아래 그림과 같이 1×1 크기의 블록을 이어 붙여 만든 3 종류의 블록을 회전해서 총 12가지 모양의 블록을 만들 수 있다.

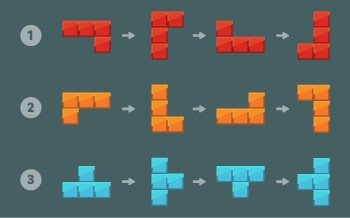
1 x 1 크기의 정사각형으로 이루어진 N x N 크기의 보드 위에 이 블록들이 배치된 채로 게임이 시작된다. (보드 위에 놓인 블록은 회전할 수 없다). 모든 블록은 블록을 구성하는 사각형들이 정확히 보드 위의 사각형에 맞도록 놓여있으며, 선 위에 걸치거나 보드를 벗어나게 놓여있는 경우는 없다.

플레이어는 위쪽에서 1 x 1 크기의 검은 블록을 떨어뜨려 쌓을 수 있다. 검은 블록은 항상 맵의 한 칸에 꽉 차게 떨어뜨려야 하며, 줄에 걸치면 안된다. 이때, 검은 블록과 기존에 놓인 블록을 합해 속이 꽉 채워진 직사각형을 만들 수 있다면 그 블록을 없앨 수 있다.

예를 들어 검은 블록을 떨어뜨려 아래와 같이 만들 경우 주황색 블록을 없앨 수 있다.

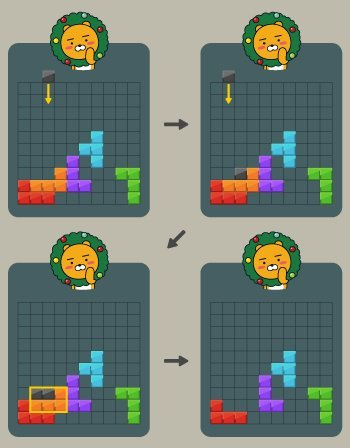
빨간 블록을 가로막던 주황색 블록이 없어졌으므로 다음과 같이 빨간 블록도 없앨 수 있다.

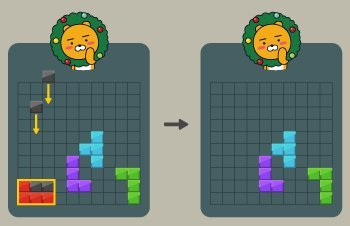
그러나 다른 블록들은 검은 블록을 떨어뜨려 직사각형으로 만들 수 없기 때문에 없앨 수 없다.

따라서 위 예시에서 없앨 수 있는 블록은 최대 2개이다.

보드 위에 놓인 블록의 상태가 담긴 2차원 배열 board가 주어질 때, 검은 블록을 떨어뜨려 없앨 수 있는 블록 개수의 최댓값을 구하라.

제한 사항

• board는 블록의 상태가 들어있는 N x N 크기 2차원 배열이다.
• N은 4 이상 50 이하다.
• board의 각 행의 원소는 0 이상 200 이하의 자연수이다.
• 0 은 빈 칸을 나타낸다.
• board에 놓여있는 각 블록은 숫자를 이용해 표현한다.
• 잘못된 블록 모양이 주어지는 경우는 없다.
• 모양에 관계 없이 서로 다른 블록은 서로 다른 숫자로 표현됩니다.
• 예를 들어 문제에 주어진 예시의 경우 다음과 같이 주어진다.

풀이

이것도 풀다가 못풀어서 구글링을 한 다음에 풀이를 본 다음에 풀었다.
이 풀이는 vector 인자 하나하나마다 검사하는 방식이다.
do ~ while 반복문을 사용했는데 중간에 블록이 없어지면 다시 처음부터 돌아가서 검사한다.
검사하는 방식은 블록을 2x3, 3x2로 분리하여 검사한다.
입력받는 int형 벡터는 전역변수인 tmp에다 복사했다.
블록을 채울 수 있는지는 판단하는 함수는 다음과 같다.

ㄴ자 블록이 3x2 블록에 채워져 있다고 가정하자 그럼 그 블록 안에서 (1,2), (1,3)에 검은 블록을 채워야 하는데, 이 컬럼 위에 다른 블록으로 막혀져 있다면(지워지지 못한 블록들) 이 3x2블록은 직사각형으로 채울 수 없다.

코드

#include <string>
#include <vector>
#include <iostream>
using namespace std;

vector<vector <int>> tmp;

bool ft_isok(int r, int c)	// 블록 내 빈 공간 위에 다른 블록으로 막혔는지 판단.
{
	for (int i = 0; i < r; i++)
		if (tmp[i][c] != 0)
			return false;
	return true;
}

bool ft_check(int r, int c, int h, int w) {
	int emp = 0;
	int default_value = -1;

	for (int i = r; i < r + h; i++) {
		for (int j = c; j < c + w; j++) {
			if (tmp[i][j] == 0) {
				if (!ft_isok(i, j))	// 빈 공간인데  위에 막혀있다면 이는 블록 채우기가 불가능하다.
					return false;
				if (++emp > 2)	// 블록 내에 빈 공간이 2개를 넘기면 직사각형으로 블록을 채울 수 없다.
					return false;
			}
			else {
				if (default_value != -1 && default_value != tmp[i][j])
					return false;
				default_value = tmp[i][j];
			}
		}
	}
	for (int i = r; i < r + h; i++)
		for (int j = c; j < c + w; j++)
			tmp[i][j] = 0;
	return true;
}

int solution(vector<vector<int>> board) {
	int answer = 0;
	tmp = board;
	int cnt, n = board.size();
	bool ret;

	do {
		cnt = 0;
		ret = false;
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				if (i <= (n - 3) && j <= (n - 2) && ft_check(i, j, 3, 2)) {
					cnt++;
					ret = true;
					break;
				}
				else if (i <= (n - 2) && j <= (n - 3) && ft_check(i, j, 2, 3)) {
					cnt++;
					ret = true;
					break;
				}
			}
			answer += cnt;
			if (ret)
				break;
		}
	} while (cnt);

	return answer;
}