배열(array)
배열은 타입이 같은 데이터들을 하나로 묶는 방법으로 인덱스와 데이터의 쌍의 집합이라고 할 수 있다.
배열에서 가능한 연산은 다음과 같다.
create(n) => n개의 요소를 가진 배열 생성 => int A[n]
retrieve(A,i) => 배열 A의 i번째 요소 반환 => A[i]
store(A,i,item) => 배열의 i번째 위치에 item 저장 => A[i] = item
배열의 i번째 요소의 저장 위치
retrieve()와 store()를 위해서는 A[i]가 저장되어 있는 위치를 알아야 접근 가능하다.
C언어를 비롯한 여러 언어에서 배열은 연속적인 메모리 공간에 할당되고 우리는 이러한 특징을 이용하여 배열의 특정 위치에 접근하는 것이 가능하다.
1차원 배열의 주소
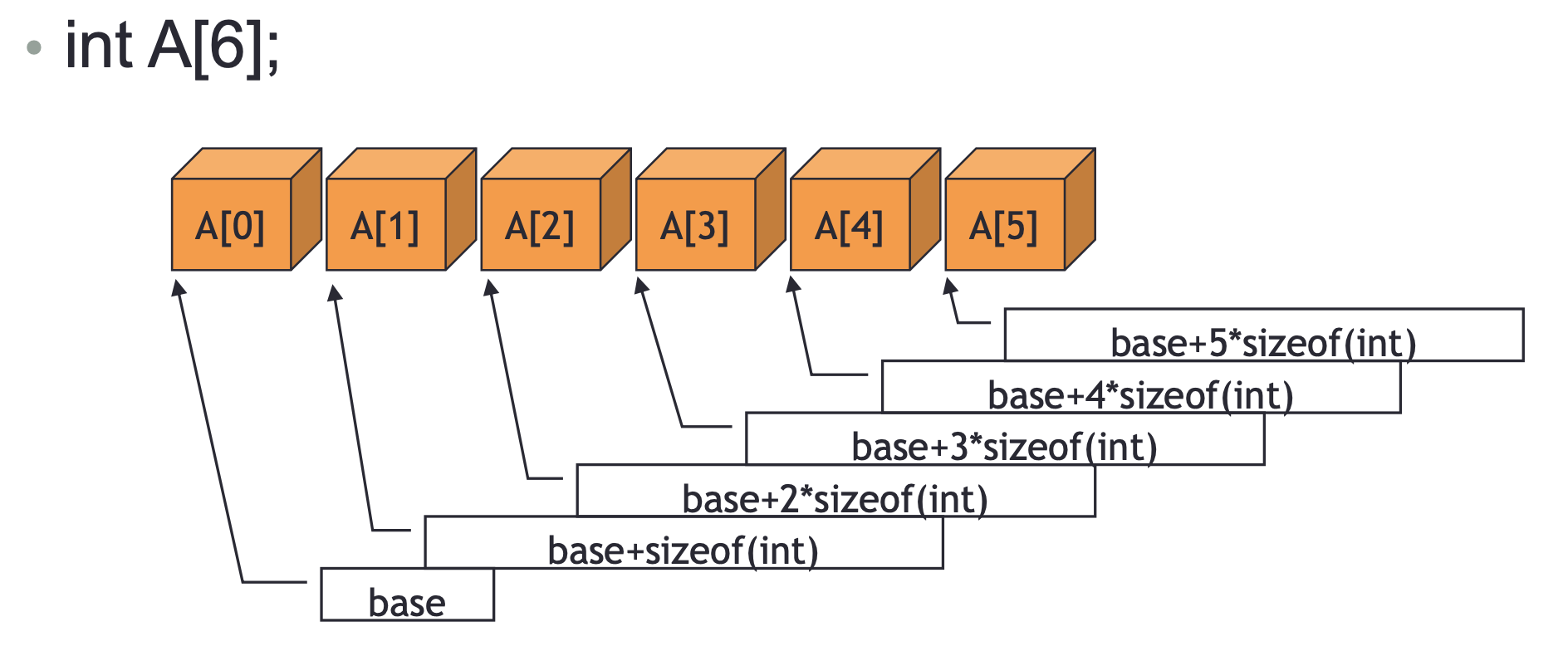
A[0]의 위치를 안다고 가정하에 base 주소라고 해보자.
그렇다면 int형 배열에서 A[0]의 다음인 A[1]의 주소는 int형의 메모리 공간만큼 이동하게 된다. 차례대로 A[2], A[3]....A[n]까지 마찬가지로 int의 메모리 공간만큼 주소가 이동될 것이다.
위와 같은 원리로 배열의 주소값을 구하는 공식은 다음과 같다.
base+n*sizeof(int)
다른 데이터 타입의 배열을 선언했다면 sizeof 연산자 안에 그 데이터 타입을 넣으면 된다.
2차원 배열의 주소
2차원 배열의 주소는 어떻게 계산할까.
사실 프로그램에서 2차원일지라도 실제 메모리상에서는 1차원적인 주소를 가지고 있다. 그렇기 때문에 2차원 배열의 주소를 구할 때는 행단위로 잘라서 한 줄로 생각하여 구하면 된다.
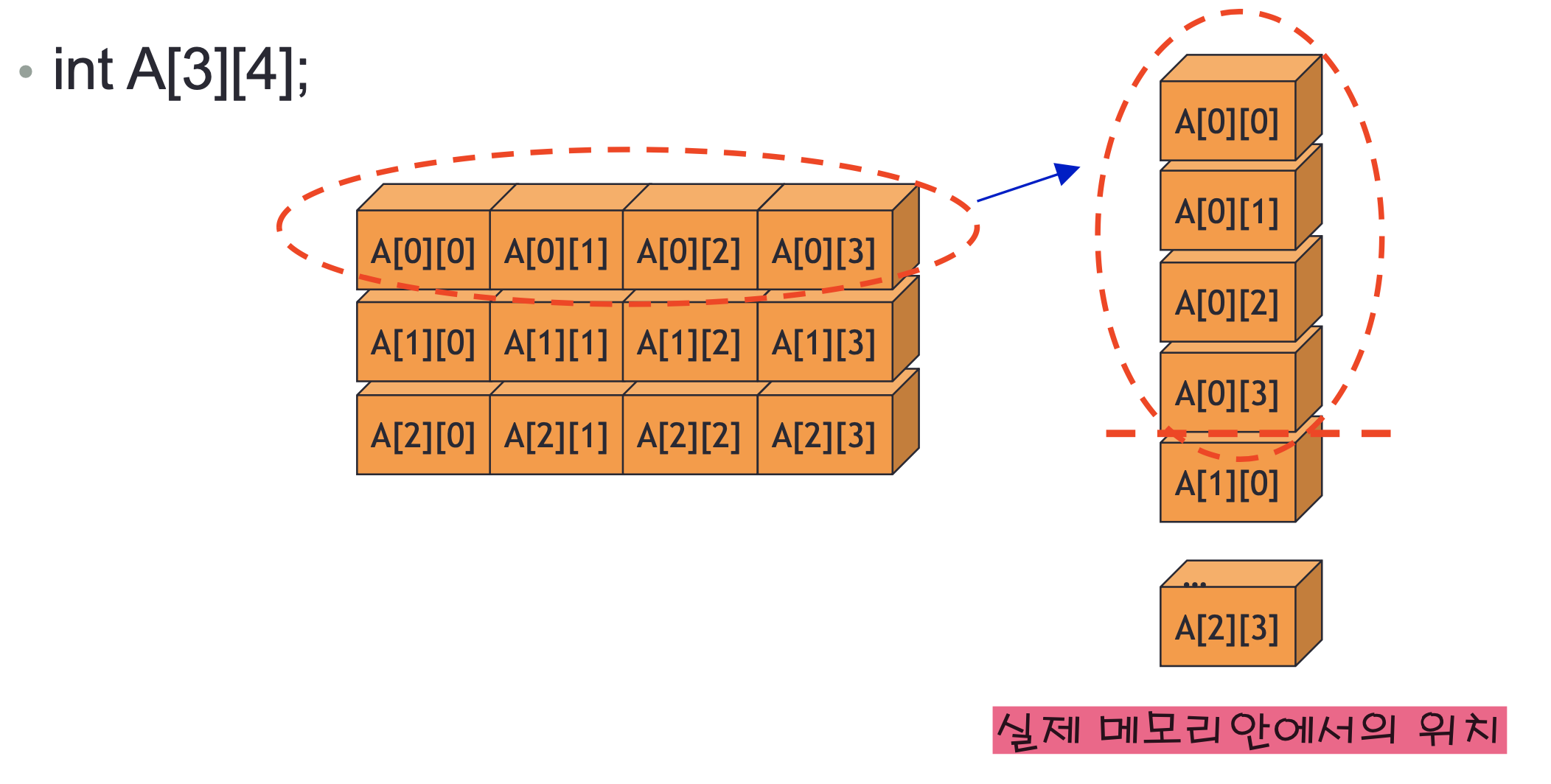
예시로 A[3][4] 배열에서 A[2][3]의 주소를 구해보자.
행 index가 2이므로 앞에 행이 2개가 더 있을 것이란 걸 알 수 있다.
또 열이 4개로 구성된 배열이기 때문에 행 하나당의 길이는 4가 될 것이다.
=> 2*4
열 index는 3이므로 앞에 열도 3개가 더 있을 것이란 걸 알 수 있다.
=> +3
위와 같은 과정으로 A[2][2]의 위치는 base+(2*4+3)sizeof(int)가 된다.
A[i][j]의 주소 => base + (i*n+j)sizeof(int)
여기서 n은 열의 개수 즉, 행의 길이를 말하는 것이다. 마찬가지로 데이터타입은 선언한 배열의 자료형에 따라 바꾸는 것이다.
n차원 배열의 주소
배열 A[upper 0][upper 1] ... [upper n-1] 에 대해, A[0][0]...[0]의 주소를 base라고 한다면
A[i0][i1]...[in-1] = base + i0 • ( upper1 • upper2 ... • upper n-1 )
+i₁ • ( upper2 • upper3 ... • upper n-1 )
+i₂ • ( upper3 • upper4 ... • upper n-1 )
....+ in-2 • ( upper n-1 )
+in-1
[응용] 2차원 배열의 모든 요소의 합 구하기
#define ROWS 2
#define COLS 3
int calc_sum(int list[], int rows, int cols)
{
int sum = 0;
for (int i = 0; i < rows; i++)
for (int j = 0; j < cols; j++)
sum += list[i * cols + j]; //2차원 배열이지만 1차원 배열로 접근 가능
return sum;
}
int main(void)
{
int num[ROWS][COLS] = { { 2, 3, 5} , {7, 9, 11} };
int sum = calc_sum((int *) num, ROWS, COLS);
printf("합 = %d \n", sum);
return 0;
}
여기서 가장 기억해야 할 것은 배열의 이름은 첫 번째 배열의 주소를 나타내는 포인터로서 쓰인다는 것.
cal_sum 함수에서는 2차원 배열을 1차원 배열로 접근하도록 설정하였다.
이러한 방법을 이용하면 배열의 차원과 크기에 상관없이 합산 함수를 사용할 수 있다는 장점이 있다. 즉, 배열의 크기를 미리 알지 못하는 상황에서 유용하게 쓸 수 있는 합산 함수이다.
그냥 이런 방식이 있다는 것 정도 알아두면 좋을 듯...
[참고자료]
교재: C언어로 쉽게 풀어쓴 자료구조
