
2.1 일차식과 일차 함수
선형 대수학 = 일차식(가장 높은 차수가 1인 다항식)이나 일차 함수를 공부하는 학문
2.2 일차 함수 표기법
일차함수의 예시)
f(x,y) = 3x + 6y + 4
2.3 행렬과 벡터
행렬 (Matrix)

행렬의 가로줄을 행(row), 세로줄을 열(column)이라고 부름
위의 행렬은 3x4행렬이라고 부른다
A21 = 2행 1열에 있는 원소
Aij = i행 j열에 있는 원소
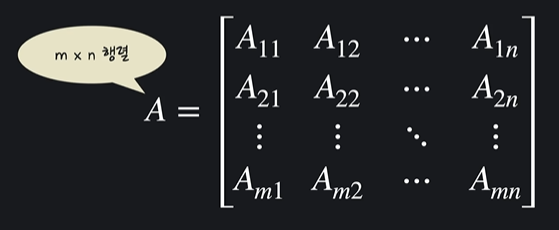
벡터 (Vector)
: 행이나 열이 하나밖에 없는 행렬
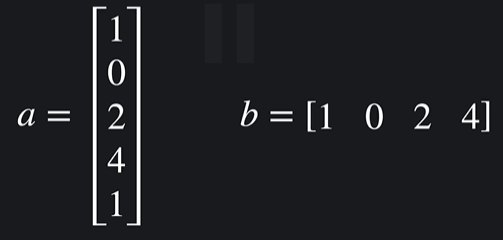
a = 열 벡터, b = 행 벡터 (열 벡터가 엄청 많아서 벡터는 그냥 열벡터라고 보면 됨)
벡터의 차원 : 원소의 개수를 얘기하면 됨
a = 5차원 벡터, b = 4차원 벡터
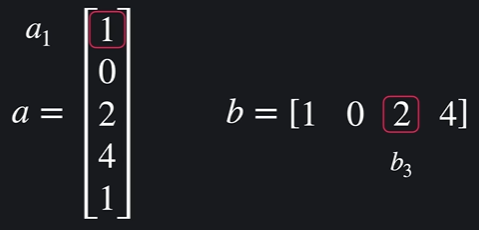
행렬은 대문자, 벡터는 소문자로 나타냄
2.4 행렬과 벡터 노트
위의 내용과 같아서 스루
2.5 numpy로 행렬 사용하기
numpy로 행렬을 만들 때에는 np.array()를 사용하고 괄호 안에 이차원 배열을 넣어주면 된다 !
4x3 배열
import numpy as np
A = np.array([
[1,-1,2],
[3,2,2],
[4,1,2],
[7,5,6]
])
Aoutput
array([[ 1, -1, 2],
[ 3, 2, 2],
[ 4, 1, 2],
[ 7, 5, 6]])3x2 배열
B = np.array([
[0,1],
[-1,3],
[5,2]
])
Boutput
array([[ 0, 1],
[-1, 3],
[ 5, 2]])랜덤하게 받아올 수도 있다 !!
이럴땐 np.random.rand(a,b)를 쓰면 되는데 a와 b는 몇차원인지 쓰면 됨
C = np.random.rand(3,5)
Coutput
array([[0.70574664, 0.80396351, 0.60129675, 0.25850687, 0.95703811],
[0.79411106, 0.73206658, 0.83526124, 0.30063362, 0.64658086],
[0.68838502, 0.37036249, 0.89833774, 0.47062098, 0.67363962]])모든 원소를 0으로 만들기
D = np.zeros((2,4))
Doutput
array([[0., 0., 0., 0.],
[0., 0., 0., 0.]])그럼 행렬의 원소를 불러오는 방법은?
ㄴ 파이썬에서 하던것처럼 A[][]로 불러오자
Aoutput
array([[ 1, -1, 2],
[ 3, 2, 2],
[ 4, 1, 2],
[ 7, 5, 6]])불러오기
A[0][2]output
22.6 (실습) numpy 행렬 연습
code
import numpy as np
# 1: 행렬 A를 정의해보세요
A = np.array([
[0,1,-1],
[1,2,3],
[2,1,0],
[-1,2,-4]
])
# 2: 행렬 B를 정의해보세요
B = np.array([
[0,2],
[1,1],
[-1,-2]
])
print(A)
print(B)
print(A[1][1]) # 3: 여기서 A의 2행 2열 원소에 접근해보세요
print(A[3][0]) # 4: 여기서 A의 4행 1열 원소에 접근해보세요2.7 행렬 연산 I (덧셈, 스칼라곱)
- 행렬 덧셈
행렬끼리 더할 땐 두 행렬의 차원이 같아야 한다 !!

- 행렬 곱셈
행렬에서 일반수는 스칼라라고 부름
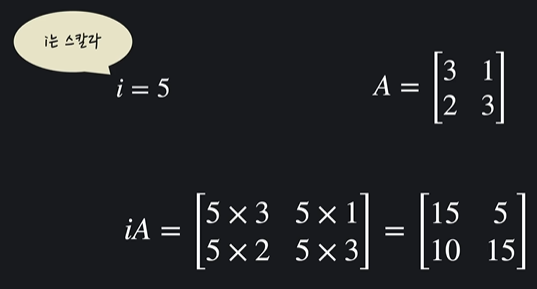
2.8 행렬 연산 I (덧셈, 스칼라곱) 노트
위와 같아서 스루
2.9 행렬 연산 II (두 행렬의 곱)
내적곱과 외적곱으로 나뉘는데 여기선 내적곱만 보겠음
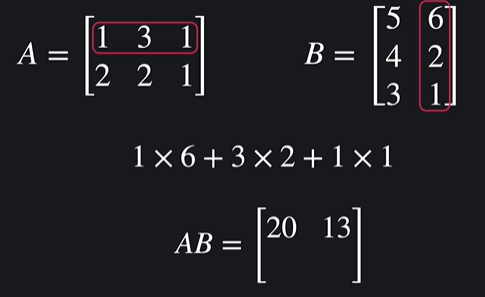
이렇게 행과 열을 곱해준 값을 더하고 넣어주면 됨

완성 !
행렬 A와 B를 곱하려면, A의 열과 B의 행의 수가 같아야함!

행렬은 AB와 BA는 다른 값이 나온다 그리고 아예 곱셈을 할 수 없을수도 있다
= 교환법칙이 성립하지 않음
2.10 행렬 연산 II (두 행렬의 곱) 노트
위와 같아서 스루
2.11 요소별 곱하기
요소별 곱하기에서는 표기를 동그라미 (∘)를 써서 표기한다
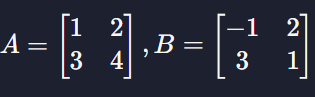
= A∘B
요소별 곱하기 = 같은 행과 열에 있는 요소들끼리 곱해서 새로운 행렬을 만드는 연산
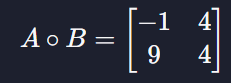
numpy로 요소별 곱하기
import numpy as np
A = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
B = np.array([
[0, 1, 2],
[2, 0, 1],
[1, 2, 0]
])A * Boutput
arrray([0, 2, 6]
[8, 0, 6]
[7, 16, 0])2.12 (실습) 행렬 연산 퀴즈
#1
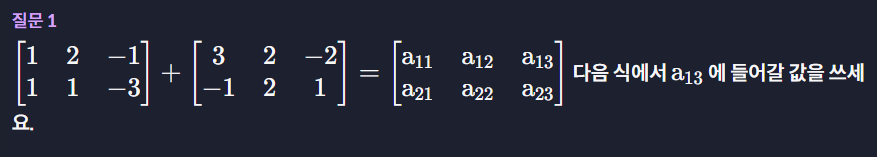
답 : -3
#2

딥 : 3
#3

답 : 5
#4

2.13 numpy로 행렬 연산하기
행렬 두개를 만들어준다
import numpy as np
A = np.array([
[1,-1,2],
[3,2,2],
[4,1,2]
])
B = np.random.rand(3,3)
A
Boutput
array([[ 1, -1, 2],
[ 3, 2, 2],
[ 4, 1, 2]])
array([[0.01491503, 0.3809792 , 0.29096529],
[0.18282684, 0.530019 , 0.00382462],
[0.1218102 , 0.03689107, 0.86506169]])행렬의 덧셈은 그냥 + 기호를 사용하면 된다
A + Boutput
array([[ 1.01491503, -0.6190208 , 2.29096529],
[ 3.18282684, 2.530019 , 2.00382462],
[ 4.1218102 , 1.03689107, 2.86506169]])스칼라 곱은 스칼라 * 행렬 형식으로 쓰면 된다
5 * Aoutput
array([[ 5, -5, 10],
[15, 10, 10],
[20, 5, 10]])행렬의 곱셈은 np.dot(행렬1, 행렬2)를 사용한다
np.dot(A,B)output
array([[ 0.07570858, -0.07525766, 2.01726404],
[ 0.65401916, 2.27675773, 2.61066848],
[ 0.48610734, 2.12771794, 2.89780915]])하지만 이것보다 더 쉬운 방법이 있는데 바로 행렬1 @ 행렬2 형식이다
A @ Boutput
array([[ 0.07570858, -0.07525766, 2.01726404],
[ 0.65401916, 2.27675773, 2.61066848],
[ 0.48610734, 2.12771794, 2.89780915]])행렬의 연산이 여러개로 있을 때에는 사칙연산 순서와 동일하게 진행된다
A @ B + (A + 2 * B)output
array([[ 1.10553863, -0.31329925, 4.59919463],
[ 4.01967285, 5.33679573, 4.61831771],
[ 4.72972774, 3.20150007, 6.62793252]])2.14 (실습) numpy로 행렬 연산 연습하기
이번 과제에서는 numpy를 사용해서 행렬 연산을 해보겠습니다. 지금 템플릿에는 행렬 4개, 각각 A,B,C,D 의 행렬이 정의되어 있는데요. 이 행렬들을 이용해서 다음과 아래 행렬 연산을 해보세요.
2A x -B x (3C + D)
code
import numpy as np
A = np.array([
[1, -1, 2],
[3, 2, 2]
])
B = np.array([
[0, 1],
[-1, 1],
[5, 2]
])
C = np.array([
[2, -1],
[-3, 3]
])
D = np.array([
[-5, 1],
[2, 0]
])
# 행렬 연산 결과를 result에 저장하세요
result = 2 * A @ (-1 * B @ (3 * C + D))
resultresult를
result = 2*A @ -B @ (3*C + D)이렇게도 쓸 수 있다
2.15 전치 행렬, 단위 행렬, 역행렬
-
전치행렬 (transposed matrix)

-
단위행렬(indentity matrix)

어떤 행렬이던 간에 단위행렬을 곱하면 기존 행렬이 유지됨
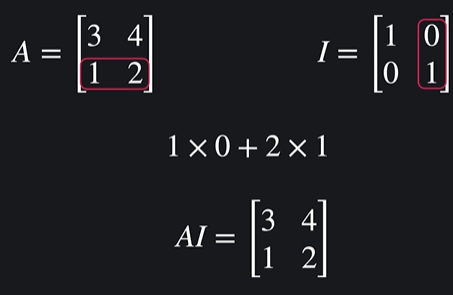
-
역행렬 (inverse matrix)
: 곱했을 때 단위행렬I가 나오게 하는 행렬
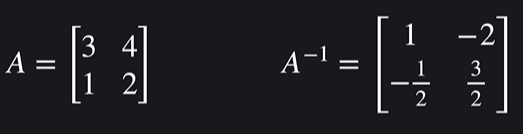
주의! 모든행렬에 역행렬이 있는 것은 아니다
2.16 전치 행렬, 단위 행렬, 역행렬 노트
위와 같아서 스루합니다요
2.17 numpy로 전치, 단위, 역행렬 사용하기
행렬 하나 만들어줌
A = np.array([
[1,-1,2],
[3,2,2],
[4,1,2]
])전치행렬을 만들때는 np.transpose()를 쓰자
A_transpose = np.transpose(A)
A_transposeoutput
array([[ 1, 3, 4],
[-1, 2, 1],
[ 2, 2, 2]])하지만 np.transpose()보다 더 간편한 방법이 이뜸 !! 바로 .T이다
A.Toutput
array([[ 1, 3, 4],
[-1, 2, 1],
[ 2, 2, 2]])ㄴ 역시 같은 값이 나온다
단위행렬은 np.identity(차원수)로 만들 수 있다
I = np.identity(3)
Ioutput
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])확인해보기 !!
A @ Ioutput
array([[ 1., -1., 2.],
[ 3., 2., 2.],
[ 4., 1., 2.]])역행렬을 만들 때에는 np.linalg.pinv()를 쓰면 된다
A_inverse = np.linalg.pinv(A)
A_inverseoutput
array([[-0.2, -0.4, 0.6],
[-0.2, 0.6, -0.4],
[ 0.5, 0.5, -0.5]])하지만 여기서 pinv()는 역행렬이 없는 경우에도 역행렬과 가장 비슷한 값을 내보내준다
역행렬이 맞는지 아닌지 확인하는 방법은 원래 행렬과 역행렬을 곱했을 때 단위행렬이 나오나 보는 것 !!
A @ A_inverseoutput
array([[ 1.00000000e+00, 5.55111512e-16, -8.88178420e-16],
[ 0.00000000e+00, 1.00000000e+00, -8.88178420e-16],
[ 0.00000000e+00, 3.33066907e-16, 1.00000000e+00]])여기선 나오지 않았는데 왜냐? pinv()의 특성 때문 ~~
2.18 (실습) numpy로 전치, 단위, 역행렬 연습
이번 과제에서는 지금까지 배운 모든 내용들을 종합해서 복잡한 행렬 연산을 numpy를 사용해서 계산해 보겠습니다. 행렬
A,B,C,D 는 저희가 이미 정의해놨고요. 여러분들은 지금까지 배운 내용을 종합하셔서 아래 행렬 연산을 numpy로 작성하시면 됩니다.
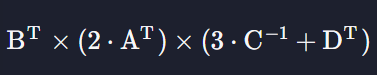
code
import numpy as np
A = np.array([
[1, -1, 2],
[3, 2, 2]
])
B = np.array([
[0, 1],
[-1, 1],
[5, 2]
])
C = np.array([
[2, -1],
[-3, 3]
])
D = np.array([
[-5, 1],
[2, 0]
])
A_trans = np.transpose(A)
B_trans = np.transpose(B)
C_inverse = np.linalg.pinv(C)
D_trans = np.transpose(D)
result = B_trans @ (2 * A_trans) @ (3 * C_inverse + D_trans)
resultresult 값을
result = B.T @ (2*A.T) @ (3*np.linalg.pinv(C) + D.T)이렇게 할 수도 있구나 !!
2.19 선형대수학과 행렬/벡터

일차식이 아무리 많아도 행렬과 벡터를 쓰면 하나의 식으로 요약할 수 있다 !
2.20 선형대수학이 머신 러닝에 필요한 이유
ex) 아파트 가격 예측
집값 = 크기 x a1 + 지하철 역 거리 x a2 + 층수 x a3

이 일차식들을 행렬과 벡터로 나타낼 수 있다 !
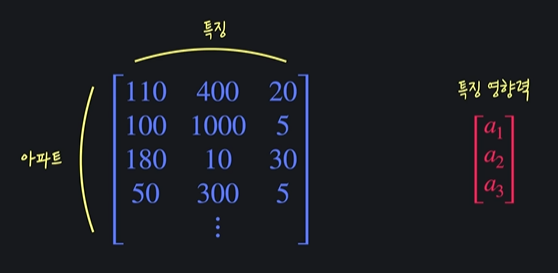
ㄴ 여기서 왼쪽 행렬을 X, 오른쪽 벡터를 a라고 하면
모든 집값은 Xa가 된다 !

