
3.1 함수
함수
ex) y = 3x + 6
-> 10이라는 input이 들어가면 36이라는 output이 나온다
주의! 하나의 input에 대해서 하나의 output만 나온다 !!
함수가 아닌 경우 )

하나의 인풋에 두개의 아웃풋이 나오기 때문에 함수가 아닌 경우이다
인풋이 여러개일 수도 있다 !

이런 함수는 다변수함수라고 한다
- 현실 세계에서의 함수

3.2 그래프
그래프 = 수학 식을 시각적으로 표현하는 방법
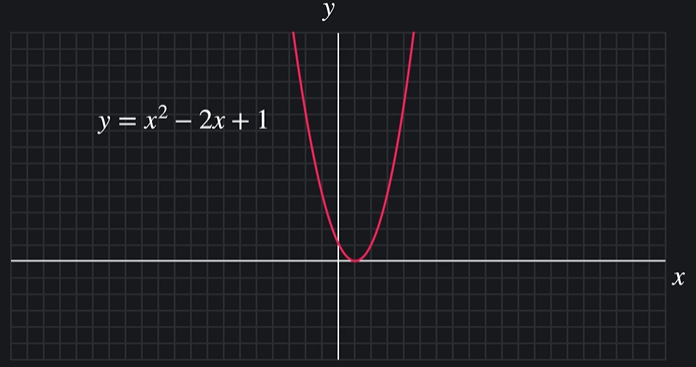
그래프를 그리는 이유 : 함수의 특징들을 간편하게 보기 위해서
3.3 평균 변화율
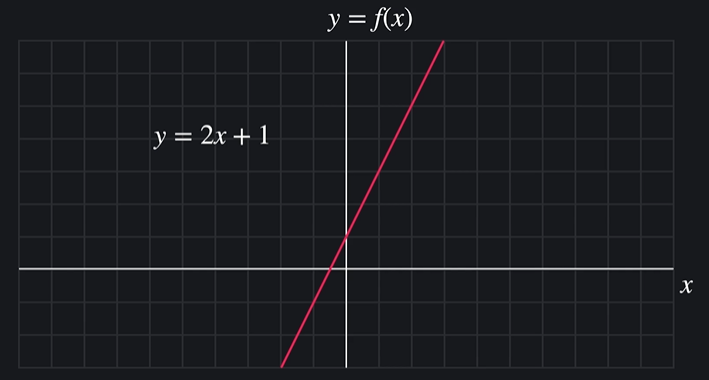
ㄴ 그래프에서 기울기는 x가 변화할 때, y는 얼마나 빠르게 변하는지 나타냄
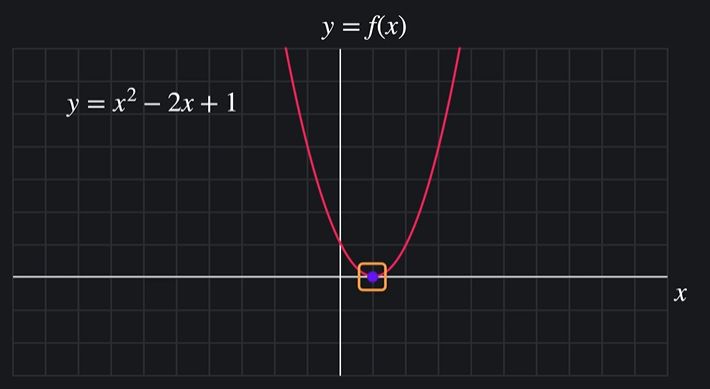
이 함수의 기울기는 함수가 곡선이라 구하기가 애매함
지점에서의 기울기를 구할 때에는 그 지점에 직선을 그어서 기울기를 구한다
ex)
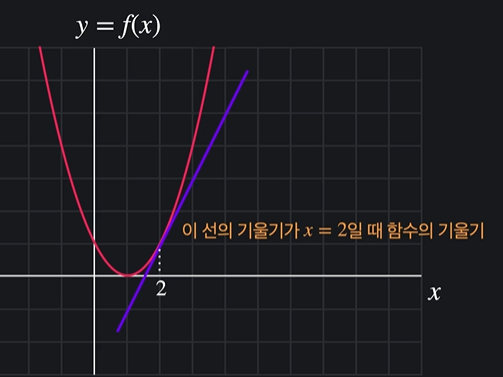
이러기 위해선 순간 변화율을 알아야 하고 순간 변화율을 알기 위해서는 평균 변화율을 알아야 한다.
평균 변화율 = f(b) - f(a) / b - a = f(a+h) - f(a) / h
3.4 순간 변화율
limit으로 표현 가능
순간 변화율 = 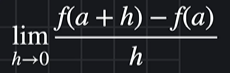
3.5 미분
f(x) = x^2 - 2x + 1 의 순간 변화율은 2x - 2 이다
이를 f'(x) 라고 부른다. 이는 기존 f(x) 의 미분이다 !
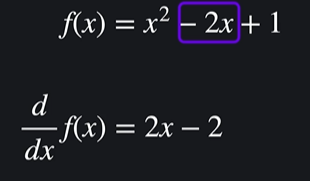
ex) f(x) = -x^4 + 2x^3 + 2x^2 + 1 의 미분은
f'(x) = -4x^3 + 6x^2 + 4x 가 된다 !
3.6 미분 노트
위와 같아서 스루한다 !!
3.7 가장 가파른 방향 (2차원)
기울기가 양수면 x가 커질 때 y가 커진다
그래프를 가장 가파르게 올라가고 싶으면 어떻게 해야할까?
기울기가 양수일 때는 양의 방향으로 움직이면 가장 가파르게 갈 수 있고
기울기가 음수일 때는 음의 방향으로 움직이면 가장 가파르게 갈 수 있다 !
ㄴ 이걸 이해하는게 머신러닝에서 핵심적이라는데.. 음.. 왤까?
3.8 가장 가파른 방향 (2차원) 노트
위와 같으니 넘긴당
3.9 극소점, 극대점
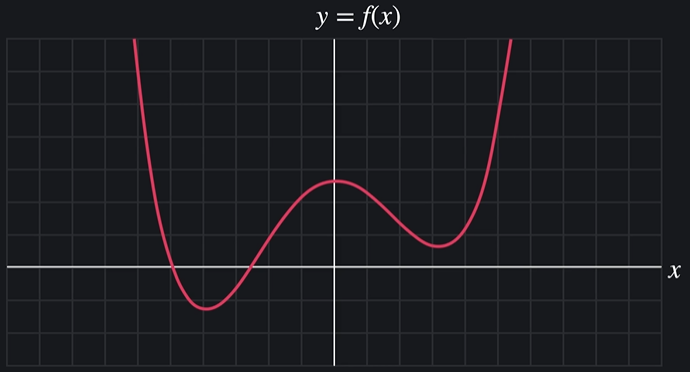
극소점 : 그래프에서 아래로 튀어나온 부분 (기울기의 양음이 바뀌는 부분)
극소점은 여러개 있을 수 있고 그 중에 가장 극소인 점을 최소점이라고 한다

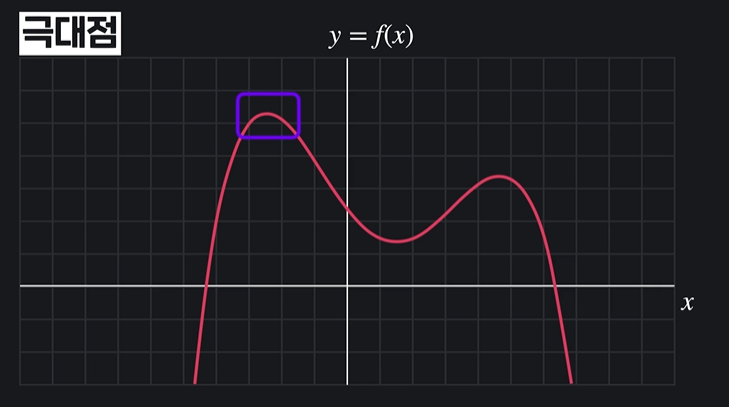
극대점은 그래프에서 위로 튀어나온 부분
극대점 역시 여러개 있을 수 있고 그 중에 가장 극대인 점을 최대점이라고 함
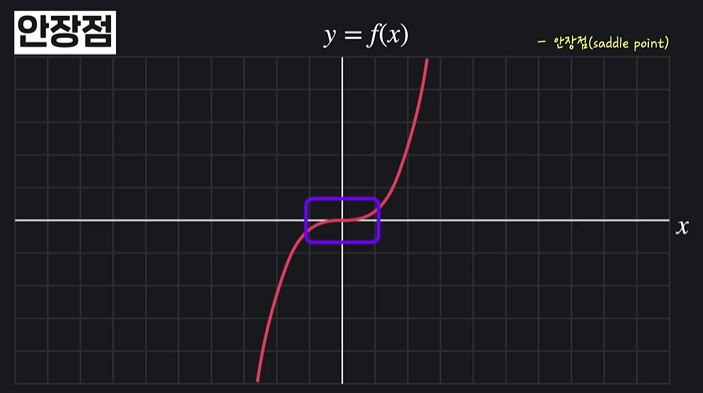
극소도, 극대도 없는 그래프도 있을 수 있는데 이런 그래프에서도 기울기의 음,양이 바뀌는데 이 점을 안장점이라고 한다
3.10 극소점, 극대점 노트
위와 같아서 스루
3.11 고차원에서 미분
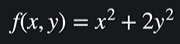
이렇게 식이 돼있다면 편미분을 해야함
편미분 : 함수를 변수 하나에 대해서만 미분
x에 대해 편미분 )
y를 상수처럼 취급해줌
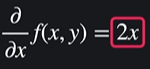
y에 대해 편미분 )
x를 상수로 취급해준다
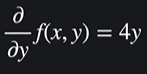
이 두 결과를 합쳐서 벡터를 만들어주고 이 벡터가 함수 f의 기울기이다
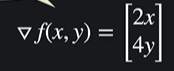
x,y가 1인 지점의 기울기를 알고싶다면 여기에 1을 대입하면 된다 !
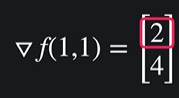
그럼 이렇게 되는데 여기서 2는 y = 1이 고정되어있고, x가 1일 떄의 함수 f의 기울기가 2라는 뜻
4는 x = 1이 고정되어있고, y가 1일 때의 함수 f의 기울기가 4라는 뜻
3.12 가장 가파른 방향 (고차원)
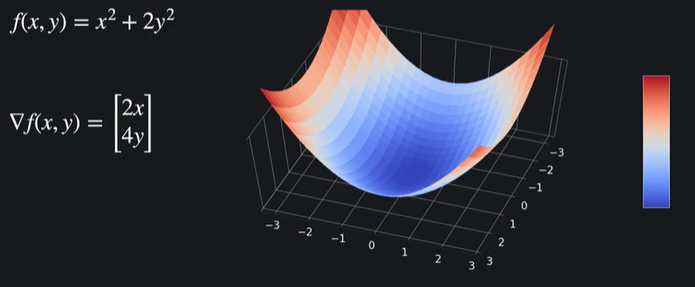
이 벡터는 해당 지점의 기울기를 알려주기도 하지만 다른 것도 알려주는데 바로 그래프가 가장 가파른 방향이 어디인지 알려줌
가장 가파르게 올라가는 방법
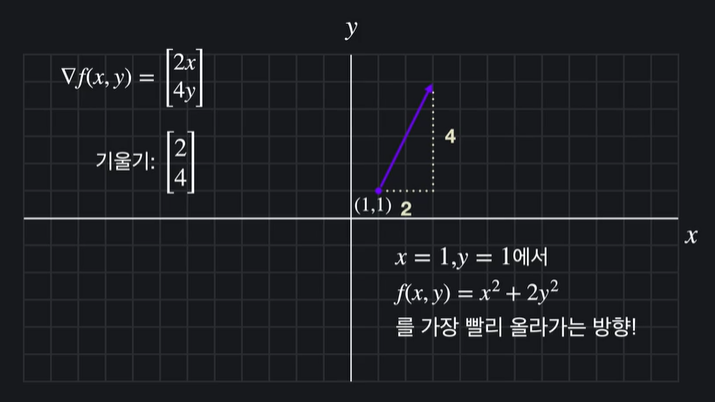
가장 가파르게 내려가는 방법은 기울기 벡터에 - 붙이기
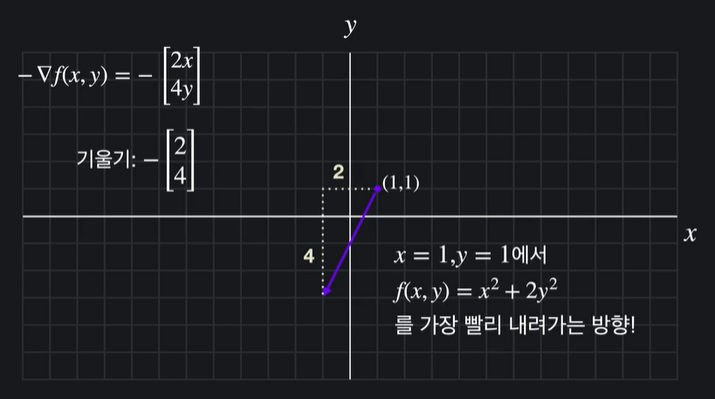
편미분 -> 기울기 벡터 -> 가장 가파른 방향
3.13 머신러닝에 미분이 필요한 이유
머신러닝 : 경험을 통해 특정 작업에 대한 성능이 좋아지는 프로그램
성능평가 ? 최적화 ? -> 함수를 통해 나옴
머신러닝을 최적화 시키려면 함수의 극소점, 극대점을 알아야하는데 이는 미분을 알아야 할 수 있다 !
