AlexNet

Lucia·2023년 7월 24일
논문리뷰
0

Article.log

목록 보기
1/4

논문링크: ImageNet Classfication with Deep Convolutional Neural Networks

AlexNet은 2012년에 열린 ILSVRC(ImageNet Large Scale Visual Recognition Challenge)에서 우승한 CNN(Convolutional Neural Networks) 모델에 대한 논문이다. 논문 저자인 Alex Krizhevsky의 이름을 딴 이 AlexNet은 CNN기반 모델의 발전에 큰 영향을 주었다고 한다.
논문의 흐름대로 내용을 정리해보고자 한다.

Abstract

ILSVRC-2010 데이터 학습
AlexNet은 ImageNet ILSVRC-2010 대회의 이미지 분류 task를 진행하며, 이 대회에서의 이미지를 학습했다. 120만 개의 이미지에서 1,000가지 종류를 분류하는 task였다.

모델 개요
6천만 개의 파라미터를 사용했고, max-pooling layer를 포함한 5개의 CNN layers, 마지막 1000-way의 softmax layer를 포함한 3개의 FC layers를 사용하여 65만 개의 뉴런으로 구성된 모델이다. 빠른 훈련을 위해 Non-saturating 뉴런을 사용하였고, overfitting을 방지하기 위해 Dropout을 사용했다. 연산은 GPU를 이용했다. 그 결과 top-1 error는 37.5%, top-5 error는 17.0%를 달성했다.

ILSVRC-2012 최종 성적
여기서 조금 변형된 모델을 사용하여 ILSVRC-2012 대회에서 top-5 error 15.3%를 달성하며 2위인 26.2% 보다 월등한 성적으로 1위를 차지했다.

1. Introduction

모델이 나오게 된 배경
큰 데이터셋을 모을 수 있게 되면서, 큰 용량의 모델이 필요하게 되었다.
이 때 CNN 모델은 깊이와 너비를 다양하게 조절할 수 있고, 이미지에 대해 정확한 예측을 한다. 따라서 기존의 비슷한 크기의 신경망에 비해 CNN은 더 적은 연결과 파라미터로 훈련이 가능하고 이론상 더 나은 효과를 보인다. 그러나 여전히 고해상도의 큰 데이터셋에 적용하기에는 힘들었으나, 다행히 GPU는 2D 합성곱 연산에 최적화되어있다.

논문의 성과

  • 매우 큰 CNN을 이용하여 ILSVRC-2010, 2012에서 기존의 기록보다 훨씬 높은 점수를 기록했다.
  • 2D 합성곱에 최적화된 GPU를 훈련에 사용하여 공식적으로 이것이 가능함을 증명했다.
  • 성능을 올리고 훈련시간을 줄일 수 있는 새로운 특징을 발견했다.
  • 논문의 신경망은 매우 커서 과대적합이 문제였지만 이를 막기 위한 다양한 기술들을 사용했다.
  • 5개의 합성곱 레이어와 3개의 FC layer를 사용했는데, 이 깊이가 매우 중요하다는 것을 알았다.
    단 하나의 합성곱 레이어를 제거했는데 (전체 파라미터의 1%도 차지하지 않음) 더 열등한 성능을 보였다.
  • GTX580 3GB GPU 2개를 사용해 5~6일 동안 훈련을 진행했고, 더욱 빠른 GPU와 큰 데이터셋이 있다면 더욱 향상될 것으로 기대된다.

2. The Dataset

ImageNet 데이터
22,000개의 카테고리로 이루어진 150만 개의 라벨링된 고해상도 이미지 데이터셋을 사용했다.
웹상에서 수집되었고, 사람에 의해 라벨링 되었다.

ILSVRC 데이터
1,000개의 class가 존재한다. 120만 개의 train data, 5만 개의 validation data, 15만 개의 test data를 사용했다.

성능평가는 top-1 error, top-5 error를 기준으로 삼았다.

전처리 작업
256 X 256 크기의 이미지로 다운 샘플링을 진행했고, 각 픽셀에 train set의 평균을 빼는 것을 제외하고는 다른 전처리 작업은 진행하지 않았다. RGB 이미지들로 학습을 진행했다.

3. The Architecture

3.1. ReLU Nonlinearity


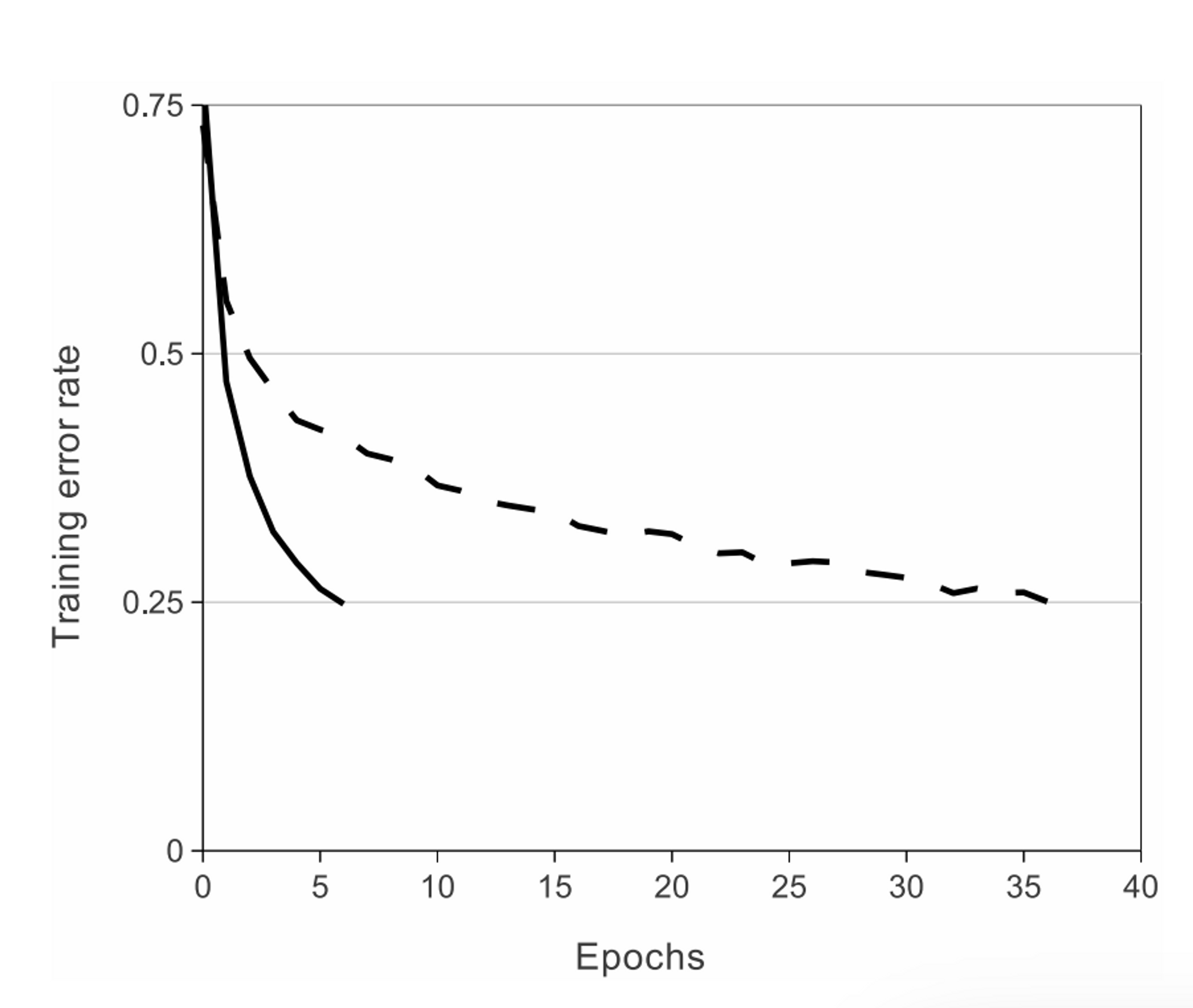
Figure 1: 기존 연구들의 방법인 tanh를 사용한 에러율과 ReLU를 사용한 에러율 비교

기존의 방법: f(x)=tanh⁡(x) or f(x)=(1+e−x)−1f(x)=\tanh(x) \ or \ f(x)=(1+e^{-x})^{-1}
연구에서는 ReLU 사용: f(x)=max⁡(0,x)f(x) = \max(0, x)

ReLU는 tanh보다 몇 배 빠른 훈련이 가능하다. ReLU 4개를 이용한 CNN 계층 4개만으로 CIFAR-10 데이터에 대해 6번의 epoch만에 25% 에러율을 달성했다. (Figure 1)

3.2. Training on Multiple GPUs

GPU 2개 사용
각 GPU에 특정 레이어만 할당함으로써 각각 절반의 뉴런들만을 할당했다.
예) layer 3의 입력은 모든 커널의 layer 2에서 받지만, layer 4의 입력은 같은 GPU에 있는 layer 3에서만 받는다. (Figure 2 참고)
이러한 방법은 교차검증에서 문제가 되지만 방대한 양의 계산이 가능하게 되었다.
→ 그 결과 에러율을 더욱 낮아졌고, 학습 시간을 축소했다.

3.3. Local Response Normalization

ReLU는 saturating을 방지하기 위해 input 정규화가 필요하지 않다.
그러나 연구에서는 다음의 local normalization이 generalization에 도움이 된다는 것을 발견했다.

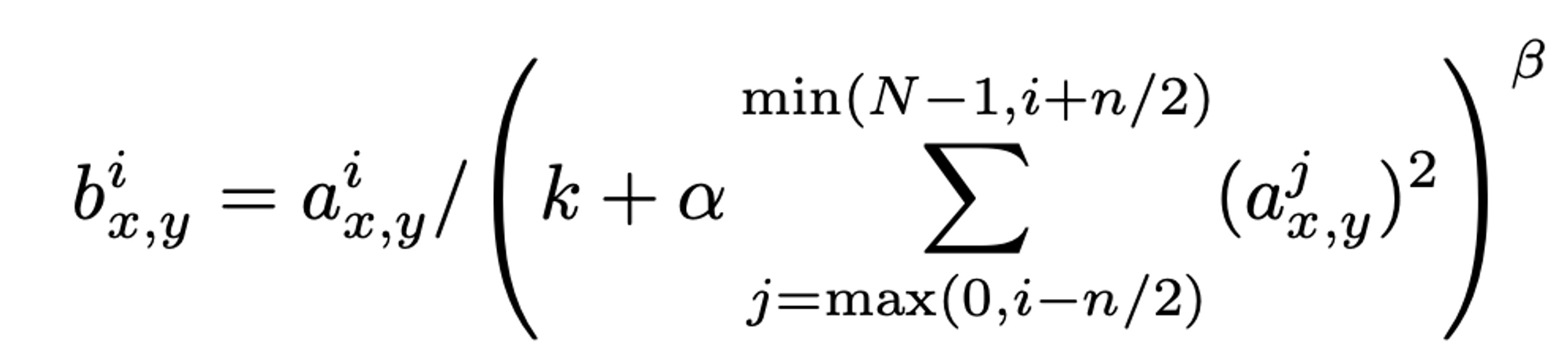
위치 (x, y)에서 커널 i를 적용한 다음 ReLU 비선형성을 적용하여 계산된 뉴런의 활동 αx,yi\alpha^i_{x,y}로 표시하는 response normalization activity bx,yib^i_{x,y}

  • 상수 k, n, α, β: validation set을 사용하여 값이 결정되는 하이퍼 파라미터
  • k = 2, n = 5, α = 10-4, β = 0.75 사용
  • 특정 계층에서 ReLU를 사용한 후 이 정규화를 적용했다. (3.5. 참조)

이를 brightness normalization라고 부른다.

→ top-1, top-5 에러율 1.4%, 1.2% 감소시켰다. CIFAR-10 데이터셋에 대해 비정규화 13%, 정규화 11%의 에러율을 달성했다.

3.4. Overlapping Pooling

기존의 방식
인접한 뉴런들은 중복되지 않게 풀링 계층을 통과시킨다.
s 픽셀 단위로 이루어진 풀링 그리드가 중심에서 x, y, z 크기의 인접 뉴런들을 요약한다.
만약 s = z로 설정한다면 CNN의 전통적인 풀링 방식이 된다.

논문의 방식
s = 2, z = 3으로 s < z가 되게 설정하여 풀링되는 뉴런들의 중복을 허용했다.
(= 풀링할 때 겹쳐지도록 설정했다는 뜻)

→ top-1, top-5의 에러율을 각각 0.4%, 0.3%만큼 낮췄다. 또한 이러한 방식이 과적합을 방지한다는 것도 발견했다.

3.5. Overall Architecture


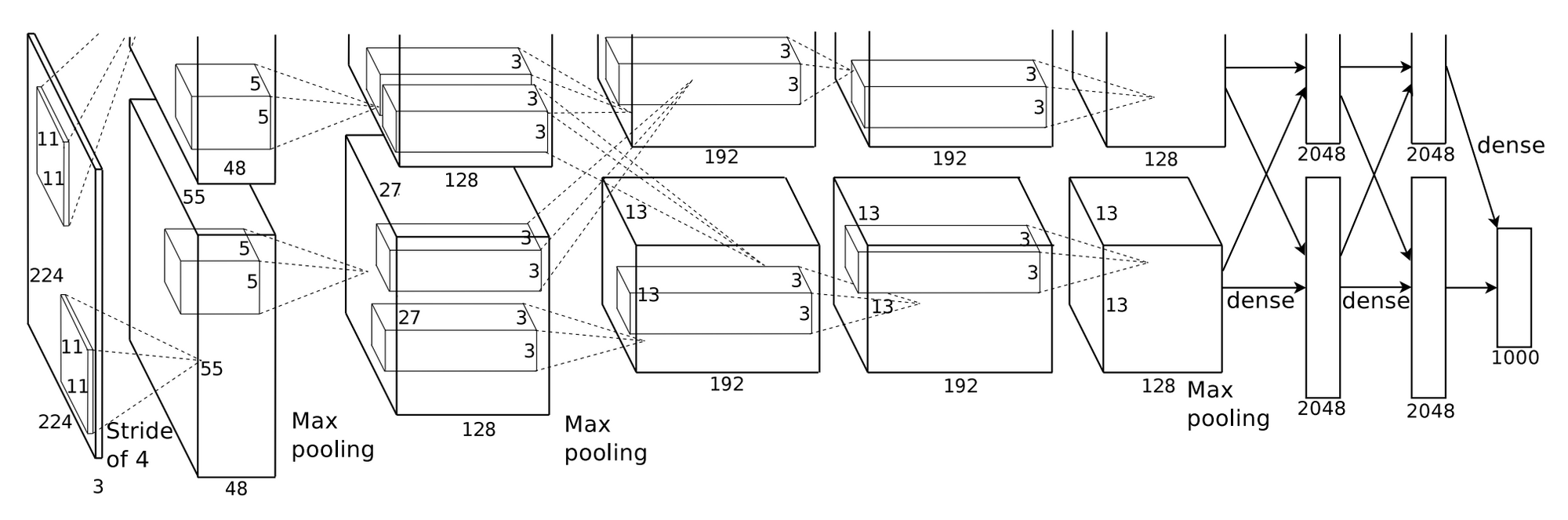
Figure 2

구성 개괄

  • 5개의 합성곱 layer와 3개의 FC layer로 총 8개의 layer로 구성된다.
  • 마지막 softmax layer는 1,000개의 클래스를 구별하기 위해 1000-way로 구성했다.
  • 2, 4, 5번째 합성곱 layer의 커널은 같은 GPU에 있는 이전 layer만 연결된다.
  • 3번째 layersms 2번째 layer와 연결된다.
  • FC layer 역시 이전 레이어의 모든 뉴런들과 연결된다.
  • response-normalization layer는 1, 2번째 레이어 뒤에 있고, 풀링 레이어는 response-normalization과 5번째 레이어 뒤에 있따.
  • ReLU는 모든 layer에 적용된다.

구성 세부

  1. 첫번째 합성곱 레이어는 224 X 224 X 3의 이미지 데이터를 입력으로 받아, stride = 4, 11 X 11 X 3 커널로 컨볼루션 한다. 96장의 55 X 55 피처맵이 산출된다.

    • 여기서 224 X 224 X 3으로 입력 받으면 55 X 55 X 96이 될 수 없다.
    • 추후에 227 X 227 X 3으로 수정되었다는 이야기와 zero padding을 적용했다는 이야기가 있다.
    • zero padding을 했을 경우에도 226 X 226 X 3일텐데 의문이 남는다.

  2. 두번째 합성곱 레이어는 response-normalizatoin과 풀링 레이어를 통과한 첫번째 합성곱 레이어를 입력으로 받아 5 X 5 X 48 크기의 커널로 컨볼루션한다. 256개의 피처맵을 출력한다.

  3. 세번째 합성곱 레이어는 정규화, 풀링을 통과한 두번째 레이어를 입력으로 받아 3 X 3 X 256 크기의 커널로 컨볼루션한다. 384개의 피처맵을 산출한다.

  4. 네번째 합성곱 레이어는 3 X 3 X 192 크기의 커널로 컨볼루션하고 384개 피처맵을 산출한다.

  5. 다섯번째 합성곱 레이어는 3 X 3 X 192 크기의 커널로 컨볼루션한고 256개 피처맵을 산출한다.

  6. 각각의 FC layer는 4,096개의 뉴런들로 구성되어 있다.

4. Reducting Overfitting

이 절에서는 과적합을 방지하는 두 가지 기법을 설명한다.

4.1. Data Augmentation

원본 데이터에 약간의 변형만 주어 디스크에 적재할 필요 없이 변환된 이미지를 생성했다.
GPU가 학습 중일 때 python 코드를 이용하여 CPU를 이용해 이미지를 생성하도록 구현했기 때문에 데이터 증강을 위한 계산 비용은 들지 않는다.

  1. image translations, horizontal reflections
    256 X 256 크기의 이미지에서 랜덤하게 224 X 224 크기를 추출하고 여기에 horiznotal reflections을 적용하여 학습시켰다.
    학습 샘플들은 높은 상호의존성을 보였지만 학습세트는 2,048배 증가했다.
    테스트시에는 각 모서리 4곳과 중앙의 1곳, horizontal-reflections까지 합한 총 10개로 증강된 이미지의 예측을 softmax 계층에서 평균함으로써 예측했다.

  2. 학습 데이터의 RGB 채널의 강도 변경
    학습 데이터 세트의 RGB 값에 PCA를 수행했다.
    각 학습 이미지에 평균이 0이고, 표준편차가 0.1인 가우시안 값에 비례하는 크기의 랜덤 변수와 이미지에서 발견된 주요 구성 요소의 배수를 더한다.
    따라서 각 RGB 픽셀 Ixy=[IxyR,IxyG,IxyB]TI_{xy} = [I_{xy}^R, I_{xy}^G,I_{xy}^B]^T에 [p1,p2,p3][α1λ1,α2λ2,α3λ3]T[\bold p_1,\bold p_2,\bold p_3][\alpha_1\lambda_1,\alpha_2\lambda_2,\alpha_3\lambda_3]^T를 더한다.
    pi,λi\bold p_i, \lambda_i는 i번째 고유벡터와 RGB 픽셀의 3 X 3 공분산 행렬의 고유값이다.
    αi\alpha_i는 램덤 변수다. 특정 학습 이미지가 다시 학습될 때 모든 픽셀에 대해 한 번만 그려진다.
    이 방법은 원본 이미지에 대해 대략적으로 중요한 특성을 뽑아내고 조명의 세기와 색상의 변화에 대해 변하지 않는다. 또한 top-1 error rate를 1% 넘게 낮췄다.

4.2. Dropout

각 은닉층의 뉴런들을 0.5의 확률로 0을 출력하게 한다.
드롭아웃된 뉴런들은 순전파와 역전파에 모두 관여하지 않는다.

그러므로 신경망에 입력값이 전달될 때마다 다른 구조를 띄지만 동일한 weight를 공유한다.
드롭아웃은 특정 뉴런이 다른 뉴런에 의존할 수 없기 대문에 뉴런들의 복잡한 의존성을 감소시킨다.

테스트 시에는 출력된 뉴런들에 50%만 사용했다. 이는 많은 드롭아웃 네트워크에 의해 생성된 예측 분포의 기하학적 평균을 취하는 것에 대한 합리적인 근사치다.

5. Details of learning

  • 확률적 경사하강법: batch_size = 128, momentum = 0.9, weight_decay = 0.0005
    weight_decay를 작게 사용하는 것은 단순히 규제 작용을 할 뿐만 아니라 모델의 train error도 줄인다.

  • 가중치 w의 업데이트
    vi+1:=0.9⋅vi−0.0005 ⋅ ϵ ⋅ wi−ϵ ⋅ ⋅⟨∂L∂w∣wi⟩Div_{i+1} := 0.9\cdot v_i - 0.0005\ \cdot \ \epsilon \ \cdot \ w_i- \epsilon \ \cdot \ \cdot \langle \frac{\partial L}{\partial w}|_{w_i}\rangle_{D_i}
    wi+1:=wi+vi+1w_{i+1} := w_i +v_{i+1}

    • ii: 반복횟수
    • ww: 모멘텀 변수
    • ϵ\epsilon: 학습률
    • ⋅⟨∂L∂w∣wi⟩Di\cdot \langle \frac{\partial L}{\partial w}|_{w_i}\rangle_{D_i} : wiw_i에서 계산된 목적 도함수 ww에 대하여 ii번째 배치의 평균인 DiD_i

  • 각 레이어에 대해 평균이 0이고 표준편차가 0.01인 가우시안 분포로 가중치를 초기화했다.
    2, 4, 5번째 합성곱 계층과 완전연결계층의 biases를 상수 1로 초기화했다.
    이는 ReLU에 양수의 입력을 주어 초기 단계의 학습을 가속시킨다.
    나머지 계층의 biases는 모두 0으로 초기화했다.

  • 모든 계층에 동일한 학습률을 적용했고, 훈련 내내 수동으로 조정했다.
    vaildation error가 현재 학습률에서 더 나아지지 않을때 학습률을 10으로 나누는 휴리스틱을 따랐다.
    학습률은 0.01로 시작해 종료되기까지 3회 감소했다.

  • 2개의 NVIDIA GTX 580 3GB GPUs를 이용해 5~6일에 걸쳐 120만 개의 이미지를 90epochs 정도로 학습시켰다.

6. Results

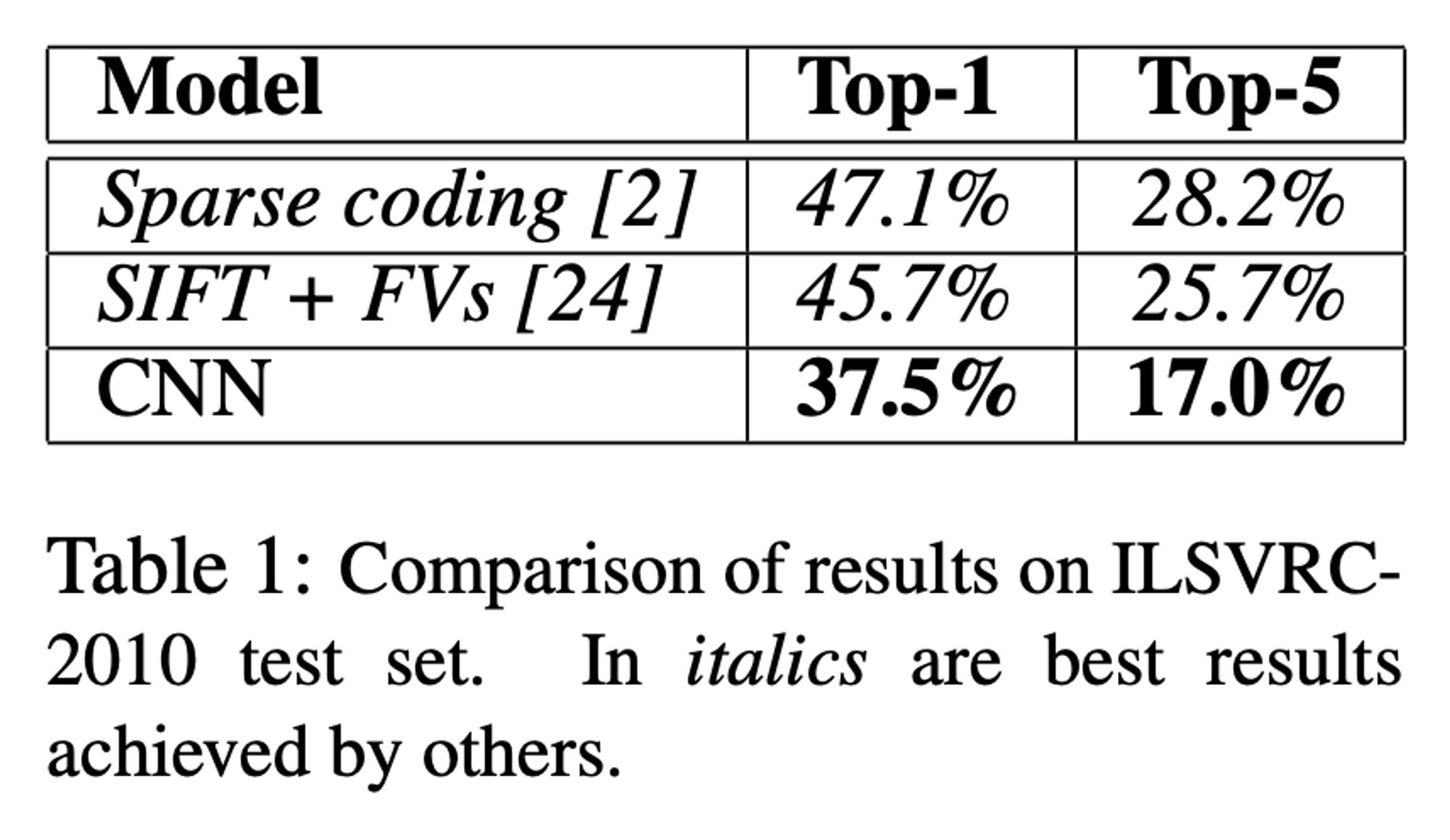
Table1: ILSVRC-2010의 결과, 이텔릭체는 다른 팀, 볼드체는 논문 저자의 팀이다.

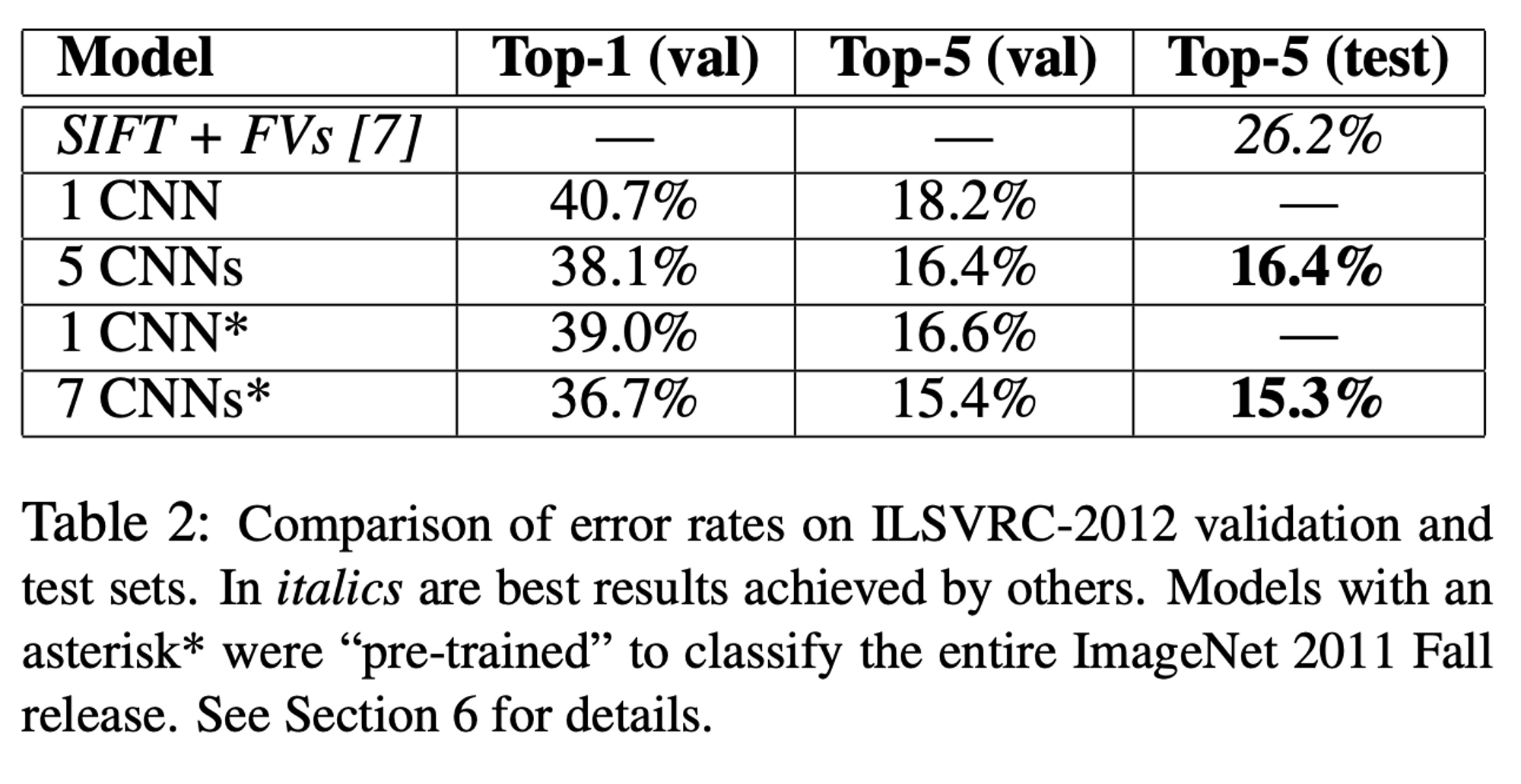
Table2: ILSVRC-2012의 결과, 이텔릭체는 다른 팀, *표시가 있는 모델은 ImageNet2011 대회에서 사전학습된 모델

  • 1 CNN의 top-5 에러율은 18.2%를 기록했고, 비슷한 CNN 5개의 예측을 평균한 모델은 16.4%를 기록했다.
  • ImageNet 2011 Fall 데이터를 분류하기 위해 만든 풀링계층 이후에 6개의 합성곱 계층을 추가한 CNN 모델을 미세조정(fine-tunning) 시켰을 때 16.6% 에러율을 달성했다.
  • 미세조정 모델과 CNN 5개의 예측을 평균한 모델을 더해 다시 예측을 평균했더니 15.3%의 에러율을 기록했다.
  • 다양한 종류의 밀접한 특성을 이용하여 Fisher Vectors를 계산해 여러 분류기의 예측을 평균한 모델은 26.2% 에러율을 기록하며 2위를 달성했다.

ImageNet Fall 2009의 에러율

  • 10,184 클래스, 890만 개의 이미지
  • 데이터의 절반은 학습에, 절반은 테스트에 사용했다.
  • 공식적인 테스트셋이 없기 때문에 이전 저자들이 사용한 데이터셋과 다르지만 결과에 미치는 영향은 없다,.
  • 위에서 언급한 풀링계층 이후 6개의 추가적인 합성곱 계층을 이은 모델로 top-1 error: 67.4%, top-5 error: 40.9%를 기록했다.
    (기존 에러율은 78.1% / 60.9%)

6.1. Qualitative Evaluations


Figure 3: 신경망 내 2개의 데이터가 연결되는 계층에서의 합성곱 커널을 보여준다.

  • 224x224x3의 이미지를 입력으로 받아 11x11x3 크기의 96개의 커널을 가진 첫 번째 합성곱 계층을 통과한 것이다. 위 48개는 GPU 1에서, 아래 48개는 CPU 2에서 작동한 것이다.

  • 여기서는 다양한 주파수, 방향, 색상들을 학습했다.

  • GPU 1은 색 정보가 거의 없지만, CPU 2는 다양한 색상을 담고 있다.

  • 이러한 특성은 랜덤한 가중치 초기화와는 무관하게 실행마다 발생한다.

  • 왼쪽: ILSVRC-2010 테스트 이미지에 대해 모델이 예측한 가장 유력한 5가지 라벨
    정답은 각 이미지의 아래에 표시되어있고, 그에 대한 확률은 빨간색 바로 표시했다.

  • 오른쪽: 첫 번째 사진은 ILSVRC-2010의 테스트 이미지, 나머지는 모델의 마지막 은닉층에서 유클리드 최소거리를 이용하여 얻은 학습 이미지

  • 왼쪽 1번 사진: 왼쪽에 있는 진드기도 신경망에서 감지할 수 있다.

  • 대부분의 top-5는 일리있는 예측을 보인다.
    (예: 고양이 종에 속하는 다른 것들이 표범의 하위 라벨들로 예측된다.)

  • 테스트 이미지가 애매모호한 경우가 존재한다. (강아지와 체리가 한 사진에 들어가 있는 것)

  • 4096개의 은닉층에서 이미지에 유도된 특성 활성화
    만약 두 이미지가 작은 Euclidean separation으로 특성이 활성화 되었다면, 우리는 신경망이 높은 수준으로 그 둘이 비슷하다고 할 수 있다.
    Figure 4의 오른쪽 사진들이 이 방법에 따라 테스트 셋의 5개의 이미지가 6개의 학습 이미지와 매우 비슷하다는 것을 보여준다.
    (두 개의 4096 차원에서 실수값 벡터의 유클리드 거리 유사도를 계산하는 것은 비효율적이지만, 오토 인코더를 이용해 짧은 이진코드로 벡터를 압축하여 훈련하면 효율적일 것)

7. Discussion

  • 깊이의 중요성
    하나의 합성곱 계층을 제거해도 결과가 나빠지는 것을 발견했다.
    (중간 1개 계층 제거했을 때 top-1 에러율 2% 증가)
  • 네트워크를 더 크게 만들고 더 오래 훈련 시킴으로 성능이 올라가지만 아직 노력이 더 필요하다.
  • 궁극적으로 정적이거나 일시적인 형태에서 많은 정보를 주는 비디오 시쿼스에서 크고 넓은 CNN을 적용하고 싶다.

ReLU나, Dropout 등 지금은 익숙한 방법들이 신선한 내용으로 나와서 신기해하며(?) 읽었습니다. CNN과 깊이의 중요성에 대해 짚어준 논문이었는데, 그래서 이 다음으로는 VGG 논문 리뷰를 올리려고 합니다.
해석이나, 내용 중 틀린 점이 있다면 댓글로 알려주세요!💡
읽어주셔서 감사합니다.😊

profile
Lucia
Data Scientist
다음 포스트

VGG

2개의 댓글

comment-user-thumbnail
happy
2023년 7월 24일

잘 읽었습니다. 좋은 정보 감사드립니다.

1개의 답글