[Lucid] Lucid vs. PyTorch 비교: LeNet-5 훈련

안암동컴맹·2025년 12월 22일

Lucid Development

목록 보기

16/20

🧪 Lucid vs. PyTorch 비교: LeNet-5 훈련

이번 개발 일지에서는 Lucid의 완성도/사용성을 현실적인 기준으로 점검하기 위해, 고전적인 CNN인 LeNet-5로 MNIST를 학습시키고 PyTorch와 결과를 비교했다. 목표는 "최신 SOTA"가 아니라, 작지만 실제적인 모델/데이터 조합에서

학습이 제대로 수렴하는지,
손실 곡선이 상식적인 모양인지,
평가 정확도가 비슷한 수준으로 나오는지,
실험이 재현 가능한 형태로 기록되는지 확인하는 것이다.

🧭 실험 원칙

프레임워크 비교에서 가장 흔한 함정은 "다른 데이터, 다른 전처리, 다른 초기화"를 섞어놓고 차이를 해석하는 것이다. 그래서 이번 실험은 동일 입력을 가장 우선순위에 두었다. MNIST를 한 번 로드한 뒤, 두 프레임워크가 동일한 x_train/y_train, x_test/y_test 배열을 사용하도록 맞췄다.

그 다음으로는 동일 모델 구조를 강제했다. Conv/Pool/FC의 채널 수와 커널 크기, 활성화 함수, 풀링 종류까지 동일하게 고정했다. 마지막으로 동일 업데이트 규칙을 적용했다. 옵티마이저는 SGD+momentum, 손실은 cross entropy, 배치 크기와 epoch 수는 동일하다.

이 세 조건이 만족되면, 남는 차이는 프레임워크 구현 디테일(연산 순서, 수치 오차, 디바이스 런타임) 쪽으로 수렴한다. 이 방향이야말로 "Lucid가 실제 학습을 끝까지 수행할 수 있는가?"라는 질문에 가장 직접적으로 답해준다.

🧾 데이터와 전처리

입력 이미지 $x \in [0,1]$ 는 MNIST 관례에 따라 평균/표준편차로 정규화했다. 정규화는 다음과 같다:

x' = \frac{x - \mu}{\sigma}, \quad \mu = 0.1307,\; \sigma = 0.3081.

이 전처리는 단순해 보이지만, 손실 곡선의 초반 형태("얼마나 빨리 떨어지는지")를 강하게 좌우한다. 따라서 두 프레임워크 모두 같은 $\mu,\sigma$ 를 사용하도록 했다.

아래는 torchvision으로 로드 → NumPy 배열로 변환 → 정규화"의 최소 코드이다(설명 목적의 축약 코드).

MNIST_MEAN = 0.1307
MNIST_STD = 0.3081

def normalize(x):
    return (x - MNIST_MEAN) / MNIST_STD

train = datasets.MNIST(root=..., train=True, download=True)
test = datasets.MNIST(root=..., train=False, download=True)

x_train = train.data.unsqueeze(1).numpy().astype("float32") / 255.0
y_train = train.targets.numpy().astype("int64")

x_test = test.data.unsqueeze(1).numpy().astype("float32") / 255.0
y_test = test.targets.numpy().astype("int64")

x_train = normalize(x_train)
x_test = normalize(x_test)

이렇게 만든 x_train/x_test는 shape이 $(N,1,28,28)$ 이고 dtype은 float32다. 레이블은 int64다. 둘 다 모델 입력에 즉시 넣을 수 있는 형태로 맞춰 놓는 것이 포인트다.

⚔️ LeNet-5 모델 구현 비교

이번 실험의 LeNet-5는 고전 설정에 맞춰 Tanh 활성화와 Average Pooling을 사용했다.

\begin{aligned} &\text{Conv}(1 \to 6, 5\times5)\;\to\;\tanh\;\to\;\text{AvgPool}(2)\\ &\to\;\text{Conv}(6 \to 16, 5\times5)\;\to\;\tanh\;\to\;\text{AvgPool}(2)\\ &\to\;\text{FC}(256\to120)\;\to\;\tanh\;\to\;\text{FC}(120\to84)\;\to\;\tanh\;\to\;\text{FC}(84\to10) \end{aligned}

Lucid에서 Conv/Pool/Linear의 구현은 아래 파일들에 있다:

Conv: lucid/nn/modules/conv.py
Pool: lucid/nn/modules/pool.py
SGD: lucid/optim/sgd.py
Cross entropy: lucid/nn/functional/_loss.py

Lucid 구현

class LeNet5(lucid.nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = lucid.nn.Conv2d(1, 6, kernel_size=5, padding=0)
        self.conv2 = lucid.nn.Conv2d(6, 16, kernel_size=5, padding=0)
        self.pool = lucid.nn.AvgPool2d(kernel_size=2, stride=2)

        self.fc1 = lucid.nn.Linear(16 * 4 * 4, 120)
        self.fc2 = lucid.nn.Linear(120, 84)
        self.fc3 = lucid.nn.Linear(84, 10)

        self.act = lucid.nn.Tanh()

    def forward(self, x):
        x = self.pool(self.act(self.conv1(x)))
        x = self.pool(self.act(self.conv2(x)))

        x = x.reshape(x.shape[0], -1)
        x = self.act(self.fc1(x))
        x = self.act(self.fc2(x))

        return self.fc3(x)

PyTorch 구현

class LeNet5(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = torch.nn.Conv2d(1, 6, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(6, 16, kernel_size=5)
        self.pool = torch.nn.AvgPool2d(kernel_size=2, stride=2)

        self.fc1 = torch.nn.Linear(16 * 4 * 4, 120)
        self.fc2 = torch.nn.Linear(120, 84)
        self.fc3 = torch.nn.Linear(84, 10)

        self.act = torch.nn.Tanh()

    def forward(self, x):
        x = self.pool(self.act(self.conv1(x)))
        x = self.pool(self.act(self.conv2(x)))

        x = torch.flatten(x, 1)
        x = self.act(self.fc1(x))
        x = self.act(self.fc2(x))

        return self.fc3(x)

두 구현의 모양은 거의 동일하다. 차이는 "Flatten 처리"에서 드러난다.

PyTorch는 torch.flatten(x, 1)을 쓴다.
Lucid는 x.reshape(x.shape[0], -1)을 쓴다.

둘 다 결과는 $(N,256)$ 로 동일하다. 이처럼 모델 코드는 의도적으로 거의 같게 유지해 비교 오차를 줄였다. 파라미터 수는 두 프레임워크 모두 44,426으로 일치한다.

📉 손실함수와 정확도

분류 손실은 cross entropy로 측정했다. 로짓 $z \in \mathbb{R}^{C}$ 에 대해 softmax 확률 $p$ 는

p_k = \frac{e^{z_k}}{\sum_{j=1}^{C} e^{z_j}},

정답 클래스 $y$ 에 대한 손실은

\mathcal{L}(z, y) = -\log p_{y}.

정확도는 가장 단순한 분류 지표로서

\text{acc} = \frac{1}{N}\sum_{i=1}^{N} \mathbb{1}[\arg\max_k z_{i,k} = y_i]

로 계산했다. 여기서 중요한 건 평가 루프에서 학습 모드 차이가 개입되지 않도록 model.eval()을 정확히 호출하는 것이다. LeNet-5 자체는 bn/dropout이 없지만, 실험 습관 차원에서 train/eval 전환은 동일하게 수행했다.

Lucid의 cross entropy 구현은 exp(logits - max)로 안정화한 softmax를 만들고, -log(prob[idx, target])로 손실을 계산한다(lucid/nn/functional/_loss.py). 즉 수식 그대로 "가능한 안정한 형태"로 구현되어 있다.

⚙️ 하이퍼파라미터 설정

이번 실험은 학습 안정성 확인이 목적이므로, 가장 단순한 설정으로 시작했다.

\eta = 0.01,\quad \mu = 0.9,\quad \text{batch}=128,\quad \text{epochs}=10,\quad \lambda = 0.

옵티마이저는 SGD+momentum이며, weight decay는 0으로 두었다. weight decay를 끄는 이유는 간단하다. 규제 항까지 섞기 시작하면, "학습이 잘 된다/안 된다"의 원인을 규제에서 찾게 되어 프레임워크의 기본 경로 검증 목적이 흐려진다.

또한 시드를 고정해 shuffle/초기화 변동이 결과를 과도하게 흔들지 않도록 했다. 완벽한 동일성은 어렵더라도, 실험을 반복했을 때 비슷한 결론이 나와야 이 실험이 의미를 가진다.

🧵 학습 루프

두 프레임워크의 학습 루프는 의도적으로 같은 형태로 유지했다.

PyTorch 학습 루프

model.train()
for x, y in train_loader:
    x, y = x.to(device), y.to(device)
    opt.zero_grad()

    logits = model(x)
    loss = torch.nn.functional.cross_entropy(logits, y)

    loss.backward()
    opt.step()

Lucid 학습 루프

model.train()
for x, y in train_loader:
    x, y = x.to("gpu"), y.to("gpu")
    opt.zero_grad()

    logits = model(x)
    loss = lucid.nn.functional.cross_entropy(logits, y)

    loss.eval()
    loss.backward()
    opt.step()

겉모양은 거의 동일하다. 하지만 Lucid 쪽에는 loss.eval() 이 들어간다. 이 한 줄이 사용성 관점에서 가장 중요한 차이였다. Lucid는 MLX 경로에서 lazy 특성을 갖기 때문에, 손실을 실제로 평가(materialize)한 뒤 역전파를 수행해야 학습 루프의 시점이 안정적으로 고정된다.

여기서 중요한 건, 이 호출이 "하드웨어 최적화" 이야기가 아니라는 점이다. 사용자가 기대하는 것은 "loss를 계산했으면 그 loss로 backward가 되겠지"라는 당연한 순서다. loss.eval()은 바로 그 순서를 강제해, 훈련 중간에 그래프가 누적되거나 시점이 꼬이는 위험을 줄인다.

📈 결과 플롯

아래 플롯은 loss(위)와 accuracy(아래)를 겹쳐 그린 결과다.

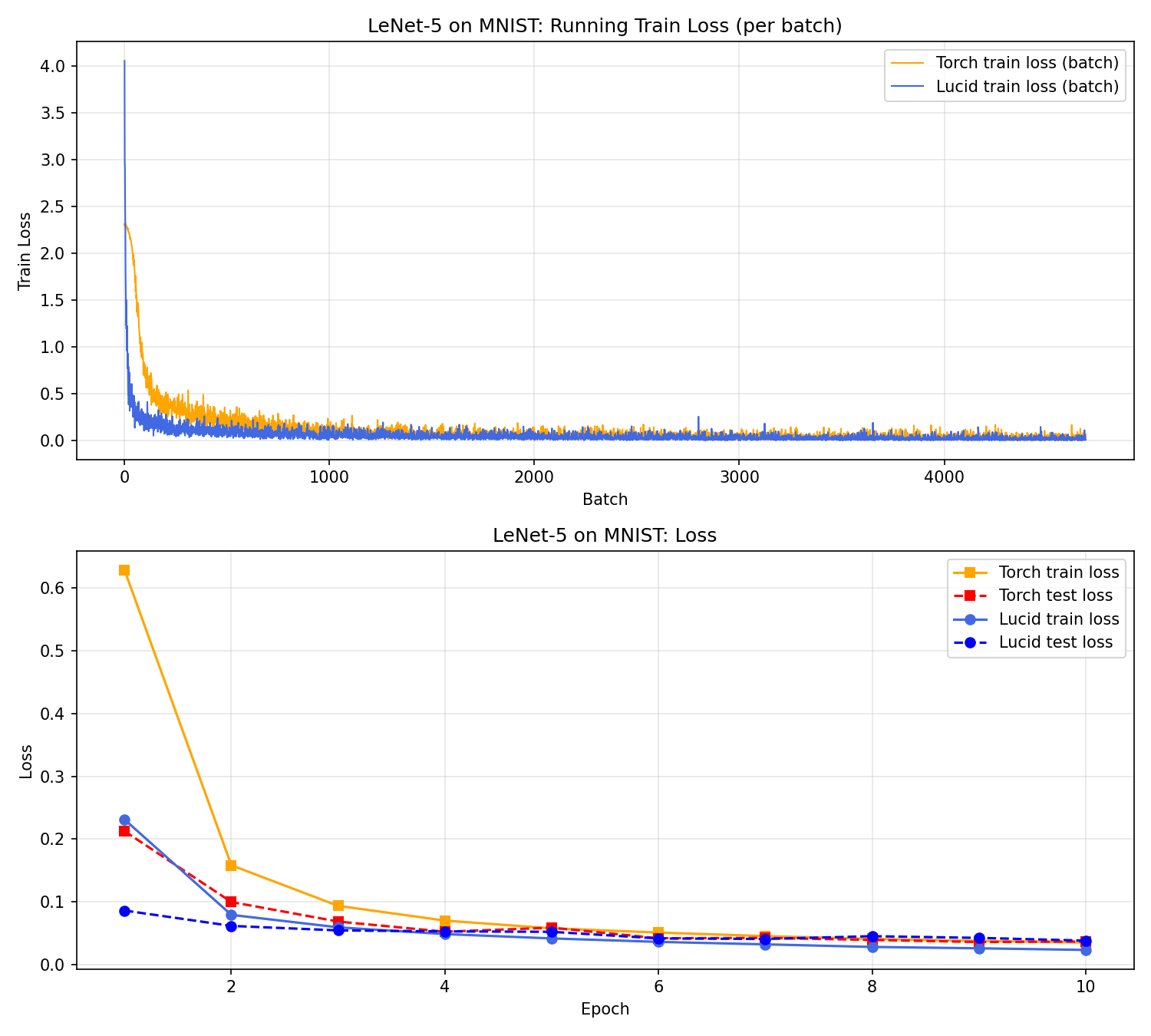
곡선이 보여주는 메시지는 간단하지만, 해석은 꽤 풍부하다. 먼저 두 프레임워크 모두 손실이 빠르게 감소하며, 테스트 정확도는 98%대에 안정적으로 도달한다. 이는 "학습이 정상적으로 수렴했다"는 가장 중요한 신호다.

초반(1–2 epoch) 에는 Lucid 쪽 손실이 더 빠르게 떨어지는 구간이 보인다. 이 차이는 초기화/셔플의 미세한 차이, 연산 순서에 따른 수치 오차 등으로 충분히 설명 가능하다. 실제로 후반부로 갈수록 두 곡선은 비슷한 기울기로 완만해지며, 7–10 epoch 구간에서는 거의 평행한 형태로 안정화된다.

또 다른 관찰 포인트는 일반화 갭이다. train acc가 test acc보다 항상 높으며, 이는 정상적인 과적합 경향을 의미한다. 하지만 gap이 과도하게 벌어지지 않아, 모델이 "학습 데이터만 기억"하는 수준으로 치우치지 않았다는 점도 확인할 수 있다. 이 실험에서는 Lucid가 더 낮은 train loss를 달성했지만, test acc/test loss는 PyTorch와 거의 비슷하다. 즉, 훈련 성능의 우세가 곧바로 일반화 우세로 이어지지 않는다는 전형적인 패턴을 보여준다.

곡선의 "부드러움"도 중요하다. 학습 도중 급격한 스파이크나 불안정한 요동이 없다는 것은 옵티마이저/손실/역전파가 안정적으로 작동한다는 신호다. 특히 Lucid의 경우 loss.eval()로 lazy 평가 타이밍을 고정했기 때문에, 손실 곡선이 매 epoch마다 안정적으로 연결된다. 이런 안정성은 단순한 숫자보다 실험 신뢰도를 높인다.

결론적으로, 플롯이 말하는 핵심은 "정상적인 수렴"과 "유사한 최종 성능"이다. 초반의 작은 차이는 실험 구성 특성으로 설명 가능하며, 두 프레임워크가 동일한 학습 궤적을 공유한다는 점이 더 중요하다.

🧾 최종 수치 요약

실험 로그에서 최종 epoch 기준 핵심 지표만 추리면 다음과 같다.

항목	Lucid	PyTorch
Train loss	0.0235	0.0353
Train acc	0.9936	0.9891
Test loss	0.0384	0.0370
Test acc	0.9866	0.9877
Params	44,426	44,426
Total epoch time (s)	30.10	14.85

성능(정확도) 관점에서 두 결과는 거의 같은 수준이며, test loss도 유사한 범위다. train loss가 더 낮다고 항상 일반화가 더 좋다는 의미는 아니므로, 여기서는 test acc/test loss가 비슷하다는 점을 더 중요한 결론으로 둔다.

epoch time 합계는 학습+평가를 모두 포함하며, 프레임워크 런타임 특성·캐시·백엔드에 따라 달라질 수 있다. 따라서 시간 값은 "빠르다/느리다"의 결론보다는, 프로파일링 대상이 생겼다는 신호로 받아들이는 편이 안전하다.

🔎 PyTorch와 Lucid의 비교

두 프레임워크는 의도적으로 "사용자 루프의 모양"을 거의 동일하게 맞출 수 있다. 그 덕분에 실험 코드도 크게 달라지지 않는다. 특히 zero_grad → forward → loss → backward → step의 리듬은 동일하다.

반면, 실제로 차이점이 드러나는 부분은 존재한다.

같은 점

모델 정의는 Module 기반이며, forward가 핵심 진입점이다.
손실/정확도 로깅은 epoch 단위로 손쉽게 가능하다.
옵티마이저의 업데이트 규칙은 동일한 형태로 적용된다(SGD+momentum).

다른 점

Lucid(MLX 경로)는 loss.eval()로 lazy 평가 시점을 확정해야 한다.
Tensor reshape/flatten API가 약간 다르며, Lucid는 reshape를 자연스럽게 쓰게 된다.
디바이스 문자열/이동 방식이 다르고, 실험 코드에서는 이를 최소한만 노출하는 것이 좋다.

이 차이는 "Lucid가 부족하다"기보다는, 백엔드 특성을 사용자 경험으로 어떻게 흡수할 것인가라는 설계 문제에 가깝다. 이번 실험은 그 설계가 "최소한의 추가(한 줄)"로 학습을 끝까지 수행할 수 있음을 보여줬다.

✅ 정리

이번 미니 실험은 “얼마나 빨리”나 “몇 % 더”보다는, 학습 루프가 끝까지 자연스럽게 이어지는가를 묻는 성격에 가깝다. 곡선의 형태가 과도하게 요동치지 않고, 손실과 정확도가 같은 방향으로 움직인다는 사실은 기술적으로는 평범하지만, 구현 관점에서는 많은 전제가 충족되어야 얻어지는 결과다. 이 점에서 Lucid의 코드 경로는 예측 가능한 흐름을 유지하고 있다고 해석할 여지가 충분하다.

다만 이런 해석은 과도하게 단정적으로 읽힐 필요는 없다. 이번 결과가 보여주는 것은 “최소 실험에서 어긋나지 않았다”는 수준이며, 그 이상은 더 다양한 실험에서 자연스럽게 드러나야 한다. 그럼에도 수식·모델·데이터·루프가 일관되게 맞물렸다는 사실은, 코드베이스가 점차 “실험을 반복 가능한 형태”로 수렴하고 있음을 시사한다. 이 비교실험이 비추는 Lucid의 완성도는 정답에 도달했다기보다, 실험 루프를 안정적으로 감당할 수 있는 단계에 가까우며, 앞으로의 확장 실험이 그 윤곽을 더 뚜렷하게 만들어 줄 것이다.

다음 단계는 자연스럽게 확장된다. 첫째, 옵티마이저를 Adam/AdamW로 바꿔 동일 프로토콜에서 수렴 궤적이 어떻게 변하는지 관찰할 필요가 있다. 둘째, LR scheduler를 붙여 학습률 곡선과 손실 곡선이 어떻게 상호작용하는지 살펴보면 "훈련 안정성"을 더 입체적으로 평가할 수 있다. 셋째, 조금 더 큰 데이터·모델로 이동하면, 지금은 보이지 않는 미세한 불안정성(예: 긴 학습에서의 누적 오차)이 드러날 가능성도 있다. 이런 확장은 성능을 과시하기보다는 루프의 내구성을 점검하는 성격으로 접근하는 것이 적절하다.