배열 (Array)
2차원 배열의 선언
1차원 List를 묶어놓은 List
2차원 이상의 다차원 List는 차원에 따라 Index를 선언
2차원 List의 선언 : 세로 길이 (행의 개수), 가로 길이 (열의 개수)를 필요로 함
Python 에서는 데이터 초기화를 통해 변수 선언과 초기화가 가능함






부분집합 합
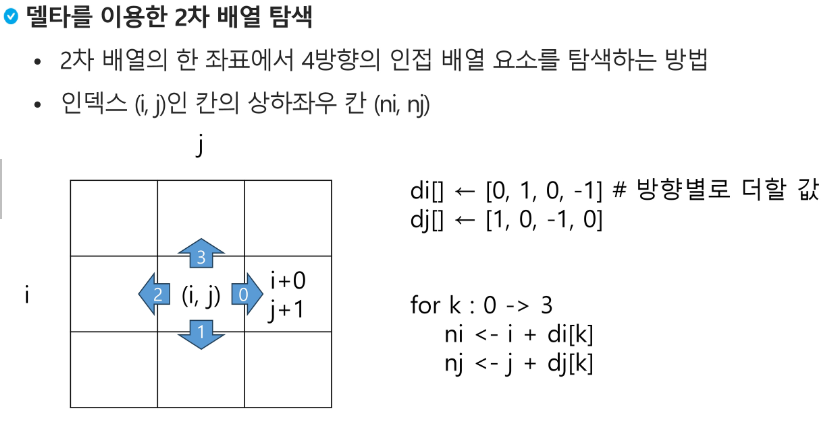
부분집합 합(Subset Sum) 문제
유한 개의 정수로 이루어진 집합이 있을 때, 이 집합의 부분집합 중에서 그 집합의 원소를 모두 더한 값이 0이 되는 경우가 있는지를 알아내는 문제
예를 들어 [-7, -3, -2, 5, 8] 라는 집합이 있을 때, [-3, -2, 5]는 이 집합의 부분집합이면서 (-3) + (-2) + 5 = 0 이므로 이 경우의 답은 참이 된다.
완전검색 기법으로 부분집합 합 문제를 풀기 위해서는, 우선 집합의 모든 부분집합을 생성한 후에 각 부분집합의 합을 계산해야 한다.
주어진 집합의 부분집합을 생성하는 방법에 대해서 생각해보자
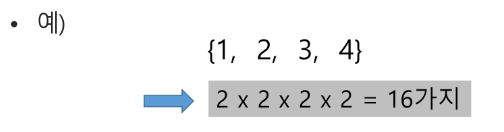
부분집합의 수
집합의 원소가 n 개일 때, 공집합을 포함한 부분집합의 수는 2의 n승 개이다.
이는 각 원소를 부분집합에 포함시키거나 포함시키지 않는 2가지 경우를 모든 원소에 적용한 경우의 수와 같다.