카운팅 정렬 (Counting Sort)
항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간에 정렬하는 효율적인 알고리즘
제한사항
-
정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능 : 각 항목의 발생 회수를 기록하기 위해, 정수 항목으로 인덱스 되는 카운트들의 배열을 사용하기 때문이다.
-
카운트들을 위한 충분한 공간을 할당한다면, 집합 내의 가장 큰 정수를 알아야 한다.

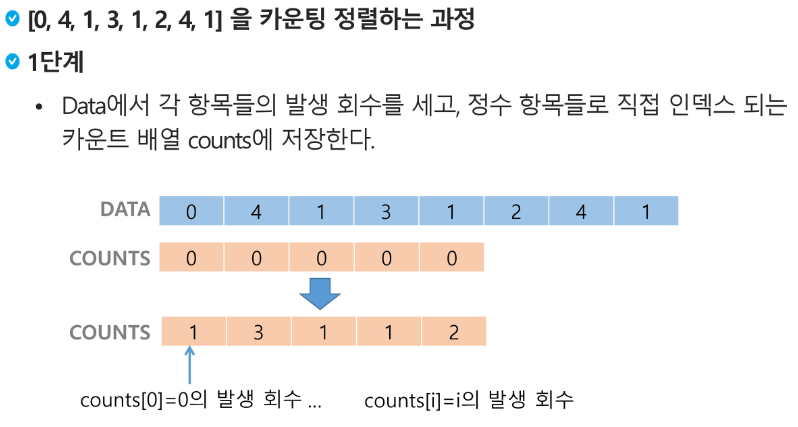
N 개의 갯수를 구하고자 할 땐 [0] * N
마지막 자리 N을 구하고자 할 땐 [0] * (N+1)
이렇게 정렬하고 0, 1, 2, 3, 4를 list.insert(a, b) 함수를 사용해도 되지 않을까?
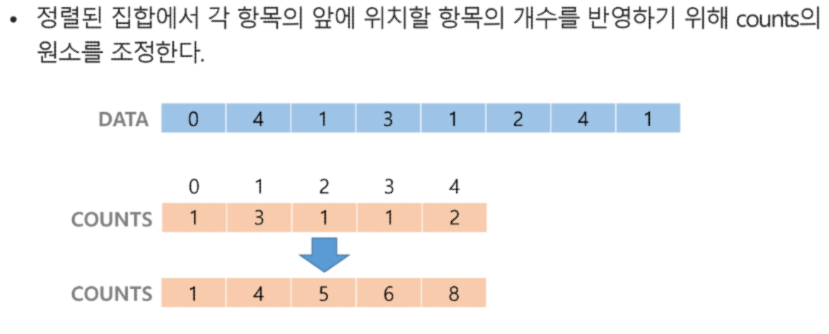
앞에 나온 값들을 더하는 누적합을 구한 것이다.
for i : 1 → k
counts[i] = counts[i-1] + counts[i] 누적합 구하는 방법
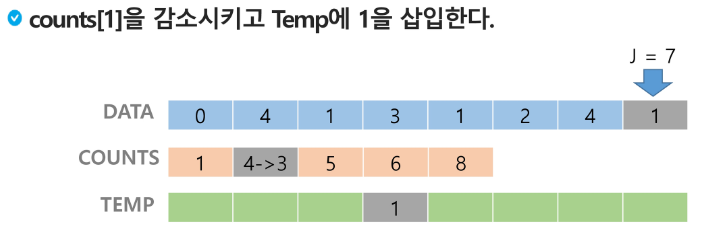

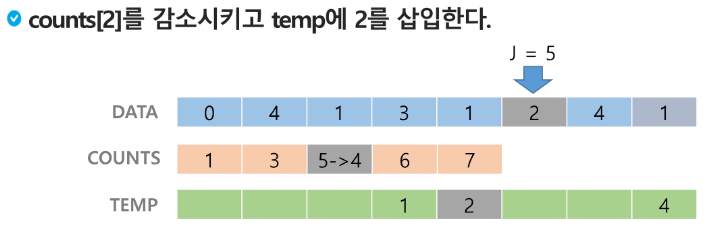

같은 숫자가 나타났을 땐 원본에서의 순서를 유지한다.



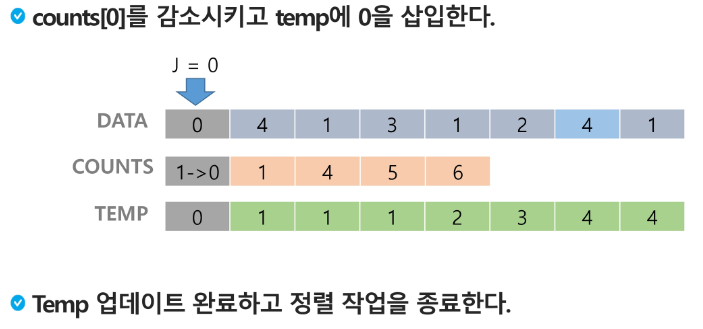
N = 6
K = 9
data = [7, 2, 4, 5, 2, 3] # 0~9, K = 9
counts = [0] * (K + 1)
temp = [0] * N # 누적합의 정렬된 결과를 넣을 빈 리스트
# counts 배열에 기록하기
for x in data:
counts[x] += 1
# counts 누적합 구하기
for i in range(1, K + 1): # 1부터 K번 인덱스까지
counts[i] = counts[i-1] + counts[i] # 누적합 구하는 방법
# data의 마지막 원소부터 정렬하기
for i in range(N-1, -1, -1) : #N-1부터 0번째까지 감소하는 형태로 더해주기
counts[data[i]] -= 1 # 개수를 인덱스로 변환 (남은 개수 계산)
temp[counts[data[i]]] = data[i]
print(*temp)
뒤에 것 부터 정렬하는 이유 : 앞에서 부터 가면 같은 값이 있을 때 순서가 바뀔 수 있다. → 원래 정렬 순서를 해치지 않음!

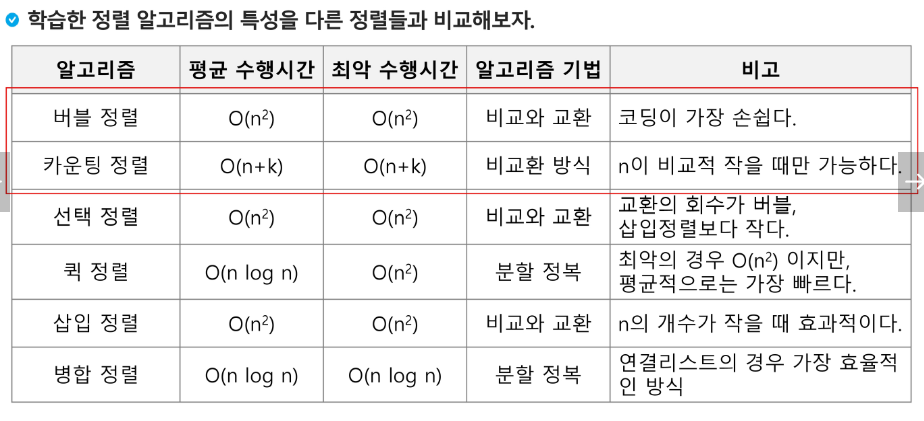
Baby-gin game
0~9 사이의 숫자 카드에서 임의의 카드 6장을 뽑았을 때, 3장의 카드가 연속적인 번호를 갖는 경우를 run 이라 하고, 3장의 카드가 동일한 번호를 갖는 경우 triplet 이라고 한다.
그리고, 6장의 카드가 run과 triplet로만 구성된 경우를 baby-gin으로 부른다.
6자리의 숫자를 입력 받아 baby-gin 여부를 판단하는 프로그램을 작성하라.

완전 검색(Exaustive Search)
완전 검색 방법은 문제의 해법으로 생각할 수 있는 모든 경우의 수를 나열해보고 확인하는 기법이다.
Brute-force 혹은 generate-and-test 기법이라고도 불리운다.
모든 경우의 수를 테스트 한 후, 최종 해법을 도출한다.
일반적으로 경우의 수가 상대적으로 작을 때 유용하다.
모든 경우의 수를 생성하고 테스트하기 때문에 수행 속도는 느리지만, 해답을 찾아내지 못할 확률이 작다.
자격검정평가 등에서 주어진 문제를 풀 때, 우선 완전 검색으로 접근하여 해답을 도출한 후, 성능 개선을 위해 다른 알고리즘을 사용하고 해답을 확인하는 것이 바람직하다.

순열 (Permutation)
서로 다른 것들 중 몇개를 뽑아서 한 줄로 나열한 것
서로 다른 n 개중 r 개를 택하는 순열은 아래와 같이 표현한다.



탐욕(Greedy) 알고리즘
탐욕 알고리즘은 최적해를 구하는 데 사용되는 근시안적인 방법
여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적으로 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
각 선택의 시점에서 이루어지는 결정은 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고 하여, 그것이 최적이라는 보장은 없다.
일반적으로 머릿속에 떠오르는 생각을 검증 없이 바로 구현하면 Greedy 접근이 된다.
탐욕 알고리즘의 동작 과정
1) 해 선택 : 현재 상태에서 부분 문제의 최적 해를 구한 뒤, 이를 부분해 집합(Solution Set)에 추가한다.
2) 실행 가능성 검사 : 새로운 부분해 집합이 실행 가능한지를 확인한다. 곧, 문제의 제약 조건을 위반하지 않는지를 검사한다.
3) 해 검사 : 새로운 부분해 집합이 문제의 해가 되는지를 확인한다. 아직 전체 문제의 해가 완성되지 않았다면 1) 해의 선택부터 다시 시작한다.


Baby-gin을 완전검색 아닌 방법으로 풀어보자
6개의 숫자는 6자리의 정수 값으로 입력된다.
counts 배열의 각 원소를 체크하여 run과 triplet 및 baby-gin 여부를 판단한다.
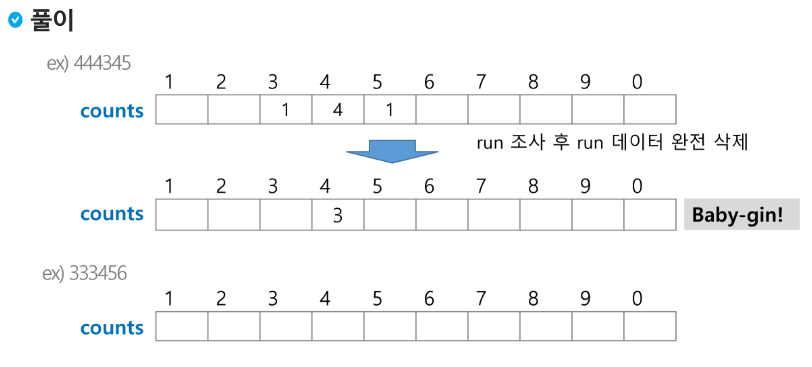
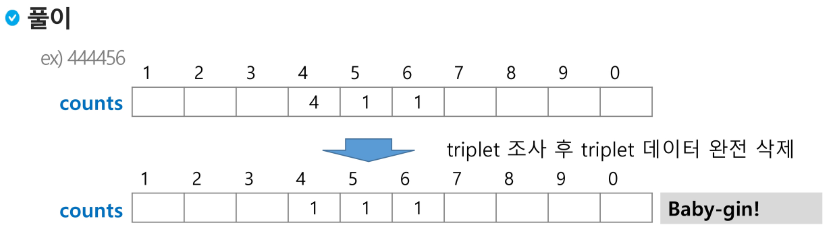
triplet 먼저 찾고 run을 찾아야 함!
444444로 triplet이 2개 존재할 수도 있으므로 한번 triplet이 발생되고 나면 그 자리에서 한번 더 검증해야 한다!


자주 실수하는 오답

