비트 연산
비트와 바이트
1 bit : 0과 1로 표현하는 정보의 단위
1 byte : 8 bit를 묶어 1 byte라고 한다.
비트연산
컴퓨터의 CPU는 0과 1로 다루어 동작되며, 내부적으로 비트 연산을 사용하여 덧셈, 뺄셈 곱셈 등을 한다.
AND 와 OR 비트 연산자 이해하기
a AND b : a, b 둘 다 1일때만 결과가 1이다. 그 외에는 0
a OR b : a, b 둘 중 하나만 1일때만 결과가 1이다. 그 외에는 0
print(0b11011110 & 0b11011)
print(0x4A3 | 25)^: XOR (엑스오어) 연산자, OR 처럼 동작되는데 둘 다 1인 경우는 0 이다. (같으면 0 다르면 1)
신기한 XOR
어떤 값이던 임의의 수로 2회 XOR 하면 원래 수로 돌아온다.
암호화 프로그램 만들기
KEY = 1004
def encode_decode(num):
return num ^ KEY
print(encode_decode(1000))
print(encode_decode(4))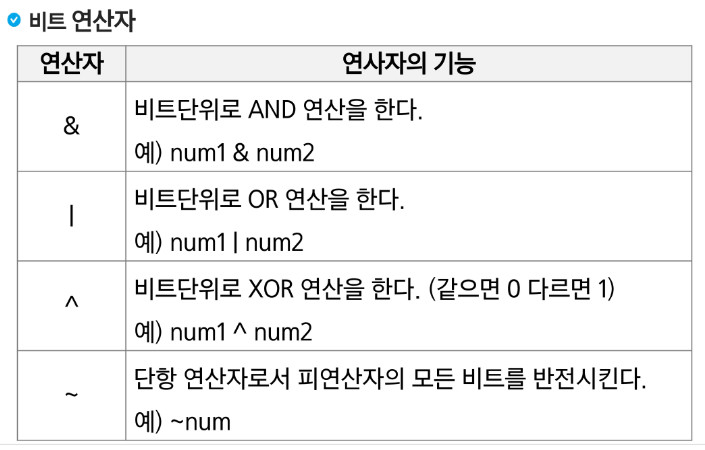

파이썬에서 2진수, 16진수, 10진수 변환하여 출력하기
2진수는 숫자 0과 소문자 b -> 0b를 접두사로 붙여 표현한다.
16진수는 숫자 0과 소문자 x -> 0x를 접두사로 붙여 표현한다.
Left 와 Right Shift 연산자
Left Shift << : 특정 수 만큼 비트를 왼쪽으로 밀어낸다. (우측에 0이 생성된다.)
Right Shift >> : 특정 수 만큼 비트를 오른쪽으로 밀어낸다. (우측 비트들이 제거된다.)

print(bin(0b1101 << 2)) # 0이 오른쪽에 생성
print(bin(0b1101 >> 2)) # 우측 비트들이 제거left shift(<<)를 이용한 프로그래밍
반복문을 이용하여 아래와 같이 출력
loop1 : 0b1 출력 (2진수와 10진수로 출력)
loop2 : 0b10 출력 (2진수와 10진수로 출력)
loop3 : 0b100 출력 (2진수와 10진수로 출력)
loop4 : 0b1000 출력 (2진수와 10진수로 출력)
loop5 : 0b100000 출력 (2진수와 10진수로 출력)
t = 1
for i in range(5):
print(bin(t), t)
t = t << 1비트 연산 응용
1 << n
2^n의 값을 갖는다.
임베디드 분야에서 계산을 빠르게 하기 위해 사용된다.
비트 연산 응용 2
i & (1 << n)
i의 n번 비트가 1인지 아닌지를 확인할 수 있다.
ex) 1101 & (1 << 2)
위 연산으로 1101에서 2번 bit가 1인지 확인 가능하다.
먼저 (1<<2)를 하면 100이 된다. 이후 1101 & 0100 = 0100 이 되며, 0100은 0보다 큰 수 이므로, n 번 비트는 1임이 확정된다. 만약 연산 결과가 0이라면, n번 비트는 0임이 확정된다.
음수 표현 방법
컴퓨터는 음수를 '2의 보수'로 관리한다.
맨 앞자리 bit(MSB)는 음수 or 양수로 구분하는 비트이다.
컴퓨터가 2의 보수를 사용하여 음수를 관리하는 이유
- 뺄셈의 연산 속도를 올릴 수 있으며, +0과 -0을 따로 취급하지 않기 위해 사용한다.
MSB : 1 -> 음수
MSB : 0 -> 양수
2의 보수 예시
10001의 2의 보수
-> 수를 모두 뒤집고 +1 을 한다.
-> 01110 + 1 = 01111
1111000 의 2의 보수
-> 수를 뒤집으면 0000111이고 +1 을 한다.
-> 0000111+1 = 0001000
신기한 2의 보수
2의 보수를 취한 수를 한번 더 2의 보수를 취하면 원래의 값으로 돌아온다.
10001의 2의 보수
-> 수를 모두 뒤집고 +1 을 한다.
-> 01110 + 1 = 01111
01111 의 2의 보수
-> 10000 + 1 = 10001
-5를 2의 보수로 표현하는 방법 (가정 : 수를 8bit로 저장하는 경우)
수 5를 2진수로 나타내면 000 0101이다. (7bit)
-5는 음수이기에 MSB는 1이다.
나머지 7bit에 대해, 수를 뒤집고 1을 더하면 된다. (2의 보수)
수 5를 뒤집으면 111 1010 이며, 1을 더하면 111 1011이 된다.
NOT 연산자
(~) NOT 연산자 : 모든 비트를 반전시킨다.
만약 8 bit일때 ~(0001 1111)이라면 값은 1110 0000이 된다.
NOT 연산자를 파이썬에서 수행하기
파이썬에서는 ~4를 수행하면 -5가 출력된다.
파이썬 ~4 를 -5로 출력하는 과정
4는 0b0100d이다. (MSB: 양수이므로 0)
NOT 연산자로 인해 뒤집으면 1011이 된다.
MSB는 1이 되었고(음수), 나머지 bit는 011 이다.
나머지 bit에 대해 2의 보수를 취하면 100 + 1 = 101 이므로 5가 된다.
따라서 -5가 된다.
비트 연산 문제 풀어보기
정수 N, M이 주어질 때, M의 이진수 표현의 마지막 N 비트가 모두 1로 켜져 있는지 아닌지를 판별하여 출력, 모두 켜져 있다면 ON 출력, 아니면 OFF를 출력
ex) 5 31
31의 이진수는 0001 1111 이다.
5개의 bit가 모두 1로 켜있다.
따라서 정답은 'ON'
M = 31
N = 5
def Test():
tar = M
for i in range(N):
if tar & 0x1 == 0:
return False
tar = tar >> 1
return True
print(Test())
실수
파이썬에서 실수 출력 방법
파이썬은 f-string 문법을 지향한다.
소수점 출력 방법
{t2:2f} : t2값을 소수점 둘째자리 까지 반올림하여 표현
파이썬에서의 실수 표현 범위를 알아보자
파이썬에서는 다른 언어와 달리 내부적으로 더 큰 규모의 자료구조를 사용해서 훨씬 넓은 범위의 실수를 표현할 수 있다.
최대로 표현할 수 있는 값은 약 1.8 10^308이고 이 이상은 inf로 표현 (참고로 1억은 1 10 ^ 8임)
최소로 표현할 수 있는 값은 약 5.0 * 10^-324 이며, 이 이하는 0으로 표현
켬퓨터는 실수를 내부적으로 근사적으로 관리한다.
실수는 정확한 값이 아니라 근사 값으로 저장되는데 이때 생기는 작은 오차가 계산 과정에서 다른 결과를 가져온다.
실수값 출력해보기
0.1이 정확히 어떤 값으로 저장되었는지, f-string을 이용하여 출력해보자
소수점 20자리 이상으로도 출력해보자
t = 0.1
print(f'{t:.2f}')근사 값으로 저장되는 원리를 알아보자