6091. 기차 사이의 파리
궁금증이 많은 한 소녀는 존 폰 노이만(John von Neumann)에게 다음과 같은 문제를 질문했다.
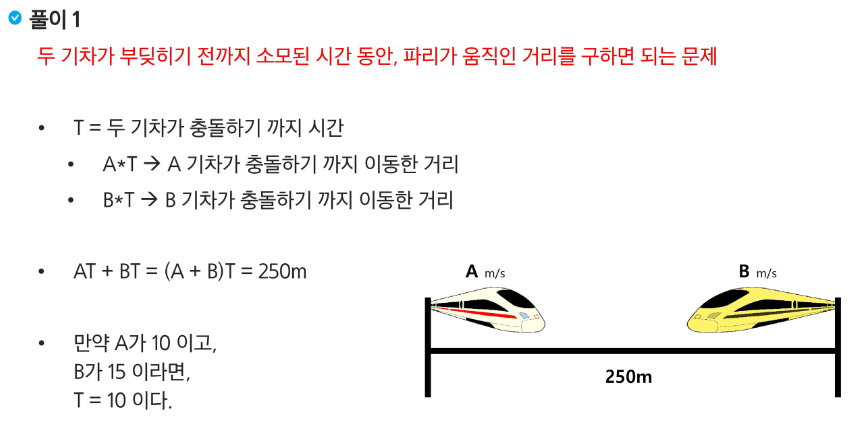
“두 기차 A, B가 서로를 향해 달리고 있다. 두 기차의 전면부는 250마일 떨어져 있고 기차 A는 시속 10마일, B는 시속 15마일로
달리고 있다.
파리가 기차 A의 전면부에서 기차 B로 시속 20마일의 속력으로 날아간다. 파리가 기차 B의 전면부에 닿으면 바로 방향을 바꿔
기차 A를 향해 같은 속력으로 날아간다.
그러다 기차 A와 B가 충돌하면 파리는 죽을 것이다. 파리는 죽기 전 까지 몇 마일의 거리를 이동했을까?”
폰 노이만은 소녀의 질문에 대해 즉시 무한 급수를 이용해 답이 200마일이라는 것을 계산해냈다.
소녀가 질문한 문제의 조금 더 일반화된 버전을 해결해보자.
[입력]
첫 번째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 네 정수 D, A, B, F (1 ≤ D ≤ 103, 1 ≤ A ≤ B < F ≤ 102) 가 주어진다.
D는 두 기차 전면부 사이의 거리, A는 기차 A의 속력, B는 기차 B의 속력, F는 파리의 속력이다.
[출력]
각 테스트 케이스마다 ‘#t’(t는 테스트케이스 번호를 의미하며 1부터 시작한다)를 출력하고 한 칸을 띄운 후,
각 테스트 케이스마다 파리가 이동한 거리를 출력한다. 정답과의 절대오차나 상대오차가 10-6 이하이면 정답으로 인정한다.

T = int(input())
for tc in range(T):
D, A, B, F = map(int, input().split())
T = D * F / (A + B)
print(f'#{tc+1} {T:.10f}')16910. 원 안의 점
N이 주어질 때, 원점을 중심으로 반지름이 N인 원 안에 포함되는 격자점(x,y 좌표가 모두 정수인 점)의 개수를 구하는 프로그램을 작성하라.
다시 말하자면, x2+y2<=N2인 격자점의 개수를 구하는 프로그램을 작성하라.
[입력]
첫 번째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 하나의 정수 N(1<=N<=200)이 주어진다.
[출력]
각 테스트 케이스마다 반지름이 N인 원 안에 포함되는 격자점의 개수를 출력한다.

T = int(input())
for tc in range(T):
N = int(input())
count = 0
for x in range(-N, N+1):
for y in range(-N, N+1):
if x**2 + y ** 2 <= N**2:
count += 1
print(f'#{tc+1} {count}')3499. 퍼펙트 셔플
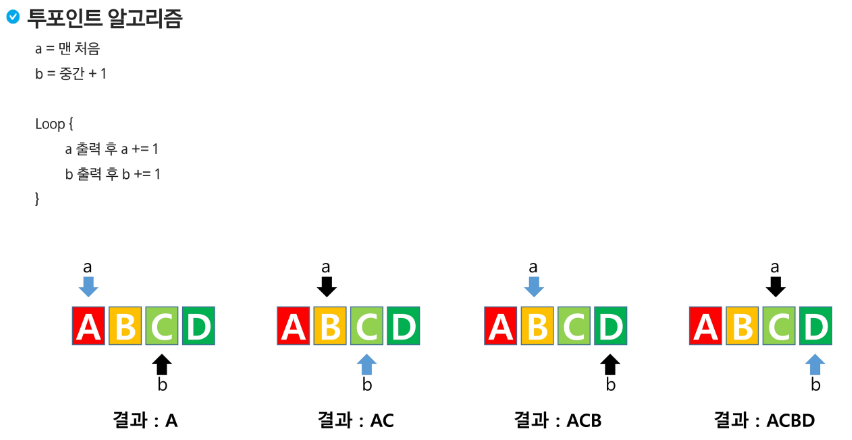
카드를 퍼펙트 셔플 한다는 것은, 카드 덱을 정확히 절반으로 나누고 나눈 것들에서 교대로 카드를 뽑아 새로운 덱을 만드는 것을 의미한다.
정확한 방식은 다음 그림과 같다.

N개의 카드가 있는 덱이 주어질 때 이를 퍼펙트 셔플하면 어떤 순서가 되는지 출력하는 프로그램을 작성하라.
만약 N이 홀수이면, 교대로 놓을 때 먼저 놓는 쪽에 한 장이 더 들어가게 하면 된다.
[입력]
첫 번째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 자연수 N(1 ≤ N ≤ 1,000)이 주어진다.
두 번째 줄에는 덱에 카드가 놓인 순서대로 N개의 카드 이름이 공백으로 구분되어 주어진다.
카드의 이름은 알파벳 대문자와 ‘-’만으로 이루어져 있으며, 길이는 80이하이다.
[출력]
각 테스트 케이스마다 주어진 덱을 퍼펙트 셔플한 결과를 한 줄에 카드 이름을 공백으로 구분하여 출력한다.
T = int(input())
N = 0
arr = []
def get_result():
a = 0
b = (len(arr) + 1) // 2
for turn in range(len(arr)):
if turn % 2 == 0:
print(arr[a], end = ' ')
a += 1
else:
print(arr[b], end = ' ')
b += 1
for tc in range(1, T+1):
N = int(input())
arr = list(map(str, input().split()))
print(f'#{tc}', end = ' ')
get_result()
print()10580. 전봇대
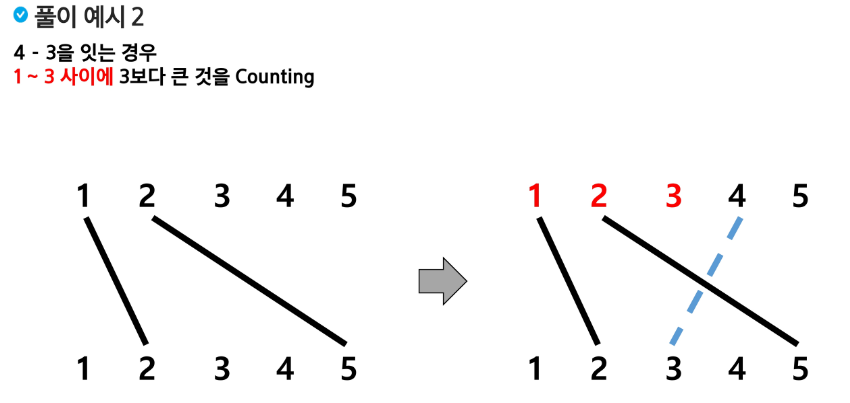
현우는 길을 가다가 전선들이 복잡하게 꼬여 있는 전봇대 두 개를 보았다. 두 전봇대는 높이가 매우 높으며, N개의 팽팽한 전선으로 연결되어 있었다. 두 전선이 끝점이 같은 경우는 없으나, 교차하는 경우는 있다. 이를 그림으로 하면 아래와 같다. (전선 3개가 있으며, 교차점 2개가 검은색으로 칠해졌다.)
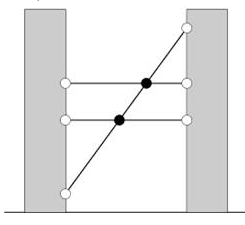
세 개 이상의 전선이 하나의 점에서 만나지 않는다고 가정하자. 이 전봇대에는 총 몇 개의 교차점이 있을까?
[입력]
첫 번째 줄에 테스트 케이스의 수 TC가 주어진다. 이후 TC개의 테스트 케이스가 새 줄로 구분되어 주어진다. 각 테스트 케이스는 다음과 같이 구성되었다.
첫 번째 줄에 주어지는 전선의 개수 N이 주어진다 (1 ≤ N ≤1000).
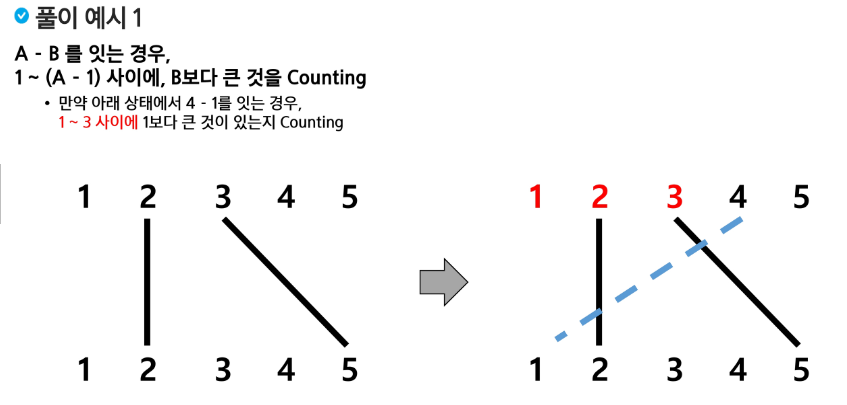
이후 N개의 줄에 두 양의 정수 Ai, Bi 가 주어진다. (1 ≤ Ai, Bi ≤ 10000)이는 i번째 전선이, 첫번째 전봇대의 Ai cm 고도에 걸려 있고, 두 번째 전봇대의 Bi cm 고도에 걸려 있음을 뜻한다.
모든 Ai는 서로 다르고, 모든 Bi 도 서로 다르다. (두 전선의 끝점이 같은 경우가 없기 때문이다.) 세 전선이 한 점에서 만나지 않게 입력이 주어진다.
[출력]
각 테스트 케이스마다 한 줄씩 교차점의 개수를 출력하라.
def get_result():
# 리스트 arr : 튜플 형태로 a 전봇대와 b 전봇대를 저장할 리스트
size = len(arr)
cnt = 0
for i in range(size):
for tar in range(i):
# a 전봇대 : 튜플의 첫번째 요소, b 전봇대 : 튜플의 두번째 요소
i_a, i_b = (arr[i][0], arr[i][1])
tar_a, tar_b = (arr[tar][0], arr[tar][1])
if i_b < tar_b:
cnt += 1
return cnt
T = int(input())
for tc in range(1, T+1):
N = int(input())
arr = []
for n in range(N):
a, b = map(int, input().split())
# 튜플 형태로 a 전봇대와 b전봇대를 append
arr.append((a, b))
arr.sort(key=lambda x : x[0]) # 첫 번째 원소를 기준으로, 오름차순 정렬
result = get_result()
print(f'#{tc} {result}')

