분할 정복

알고리즘 설계 기법의 종류

1. 전체를 다 확인한다. (Brute Force - 완전 탐색)

• 배열 : for 문, while 문

• 그래프 ( 관계가 있는 데이터 )

• BFS, DFS

→ 완전 탐색을 구현하면, 시간 or 메모리 초과 되더라!

2. 상황마다 좋은 걸 고르자 (Greedy - 그리디)

• 규칙 + 증명 → 구현

3. 큰 문제를 작은 문제로 나누어 부분적으로 해결하자 (Dynamic Programming)

• 분할 정복과 다르게 작은 문제가 중복이 여러번 발생

• 중복된 문제의 해답을 저장해놓고, 재활용하자! (Memoization)

4. 큰 문제를 작은 문제로 나누어 부분적으로 해결하자 (분할 정복)

5. 전체 중 가능성 없는 것을 빼자 (Backtracking - 빽트래킹)

→ 이 기본들을 기반으로 더 고급 알고리즘이 개발됨

분할 정복

---

병합 정렬, 퀵 정렬 → 10-15년 전 면접 단골 질문이었음, 하지만 너무 기본이고 구현할 일이 없기 때문에 최근에는 잘 활용되지 않음

가짜 동전 찾기

3-4번만에 결과를 찾을 수 있음. 24개의 동전을 12개씩으로 나누어 무게가 더 적은걸 찾고, 이를 6-6, 3-3, 1로 반복해서 찾으면 됨.

분할 정복 기법의 설계 전략

분할 (Divide) : 해결할 문제를 여러 개의 작은 부분으로 나눈다.

정복 (Conquer) : 나눈 작은 문제를 각각 해결한다.

통합 (Combine) : 해결된 답을 모은다.

하나라도 틀리면 전체 결과가 잘못 나옴

비슷한 로직을 반복!

어떤 형식으로 구현? → 재귀함수 활용!

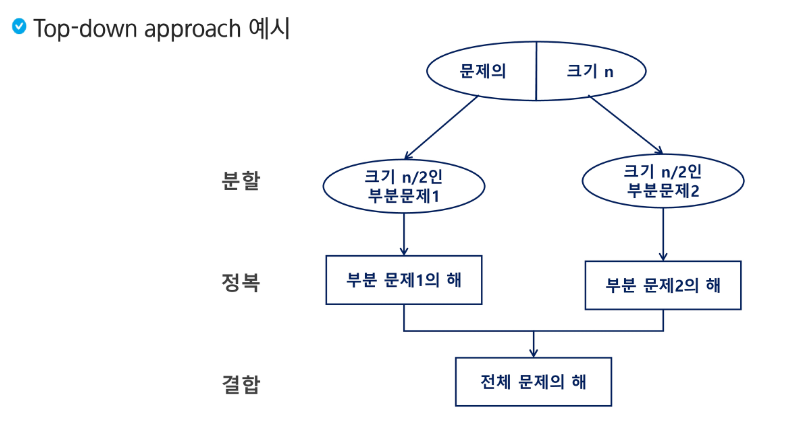
반으로 나눌 수 없을 때까지 과정을 반복

자연수 C의 n 제곱 값을 구하는 함수를 구현해보자.

병합 정렬

---

병합 정렬

병합 정렬 (Merge Sort)

여러갤의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방식

분할 정복 알고리즘 활용

자료르 최소 단위의 문제까지 나눈 후에 차례대로 정렬하여 최종 결과를 얻어냄

top-down 방식

시간 복잡도

nlog n → 비교연산 n번, 전체 분할 과정 log n 번

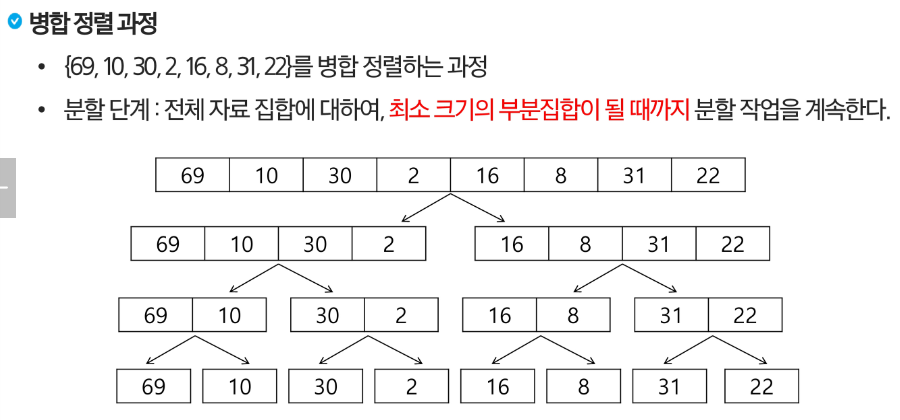
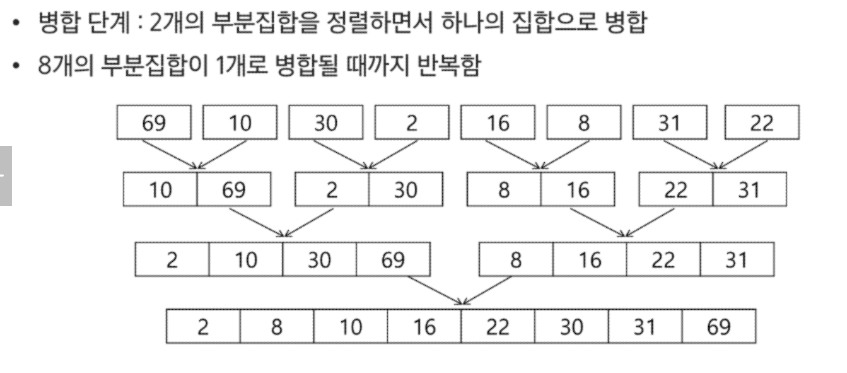
분할 과정과 병합 과정 따로 진행

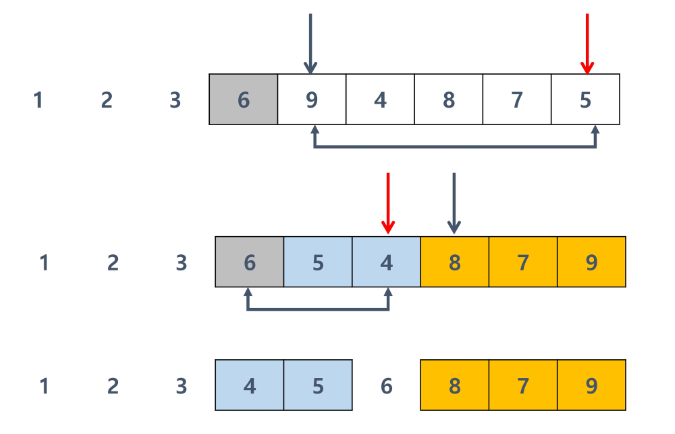
퀵 정렬

평균적으로 효율이 굉장히 좋다!

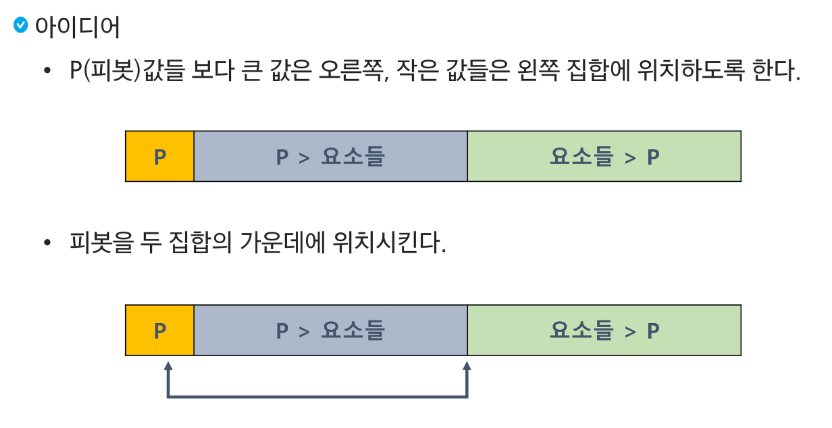
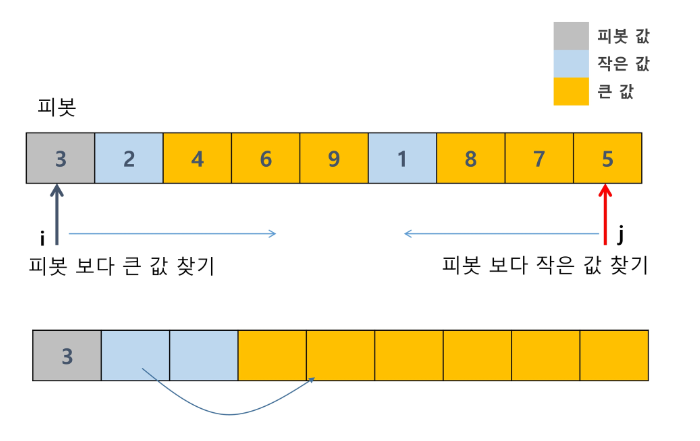
i는 맨 앞에부터, j는 맨 뒤에부터 비교하면서 큰 값을 찾는다.

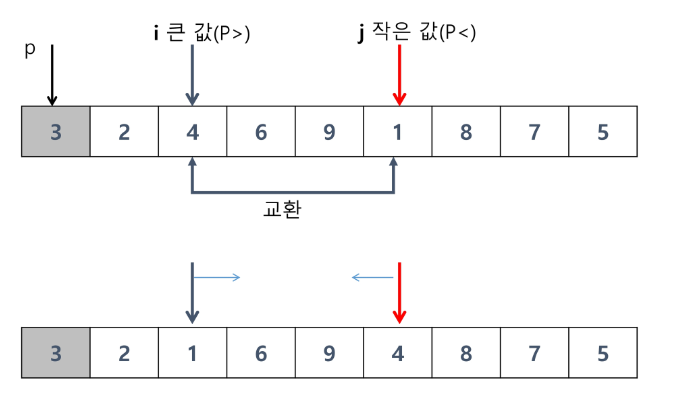
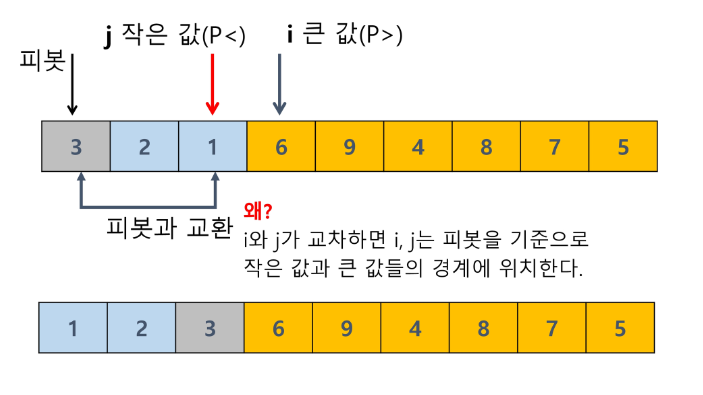
i 의 경우 p보다 큰 값을 만날때까지 증가, j의 경우 p 보다 작은 값을 만날때까지 감소

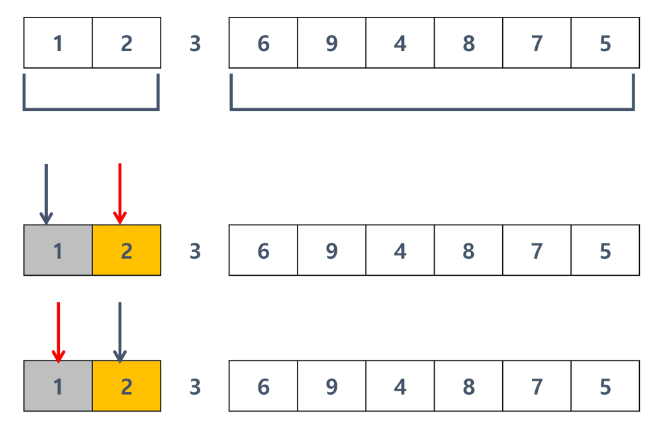
Hoare보다는 효율이 좀 떨어짐

p 보다 크면 j만 증가, p 보다 작을때까지 j를 늘려줌.

병합정렬

외부 정렬의 기본이 되는 정렬 알고리즘이다.

멀티코어 CPU나 다수의 프로세서에서 정렬 알고리즘을 병렬화하기 위해 병합 정렬 알고리즘이 활용된다.

퀵 정렬은 매우 큰 입력 데이터에 대해서 좋은 성능을 보이는 알고리즘이다.

시간 복잡도는 평균적으로는 n log n 이나, 최악의 경우에는 n**2이 걸릴 수 있다.

이진 검색 (코딩테스트 단골 문제)

---

이진 검색

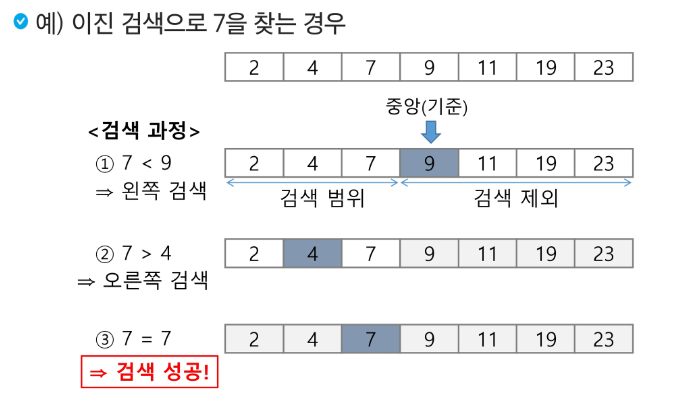
자료의 가운데에 있는 항목의 키 값과 비교하여 다음 검색의 위치를 결정하고 검색을 계속 진행하는 방법

목적 키를 찾을때까지 이진 검색을 순환적으로 반복 수행함으로써 검색 범위를 반으로 줄여가면서 보다 빠르게 검색을 수행함

이진 검색을 하기 위해서는 자료가 정렬된 상태이어야 한다.

검색 과정

1. 자료의 중앙에 있는 원소를 고른다.

2. 중앙 원소의 값과 찾고자 하는 목표 값을 비교한다.

3. 목표 값이 중앙 원소의 값보다 작으면 자료의 왼쪽 반에서 새로 검색을 수행하고, 크다면 자료의 오른쪽 반에 대해서 새로 검색을 수행한다.

4. 찾고자 하는 값을 찾을 때까지 1-3 과정을 반복한다.

arr = [324, 32, 22114, 16, 48, 93, 422, 21, 316]

# 1. 정렬된 상태의 데이터
arr.sort()

# 2. 이진 탐색 - 반복문 버전

# def binarySearch(target) :
#     # 제일 왼쪽, 오른쪽 인덱스 구하기
#
#     low = 0
#     high = len(arr) -1
#     # 탐색 횟수
#     count = 0
#
#     # 해당 숫자를 찾으면 종료
#     # 더 이상 쪼갤 수 없을 때까지 반복
#     while low <= high :
#         mid = (low + high) //2
#         count += 1
#
#         # 가운데 숫자가 정답이면 종료
#         if arr[mid] == target:
#             return mid, count
#
#         elif arr[mid] > target:
#             high = mid -1
#
#         elif arr[mid] < target:
#             low = mid + 1
#     # 못찾으면 -1 반환
#     return -1, count

# 3. 이진 검색 - 재귀함수 버전

def binarySearch(low, high, target):
    # 기저 조건 (언제까지 재귀가 반복되어야 할까?)
    if low > high :
        return -1

    # 다음 재귀 들어가기 전엔 무엇을 해야할까?
    # 정답 판별
    mid = (low + high) // 2
    if target == arr[mid]:
        return mid

    # 다음 재귀 함수 호출 (파라미터 생각 잘하기!)
    if target < arr[mid]:
        return binarySearch(low, mid-1, target)
    else:
        return binarySearch(mid +1, high, target)

    # 재귀 함수에서 돌아왔을 때 어떤 작업을 해야할까?
	# 이진 검색에서는 없다!
# 인덱스 자리 값을 구할 수 있음
print(f'21 = {binarySearch(0, len(arr)-1, 21)}')
print(f'324 = {binarySearch(0, len(arr)-1, 324)}')
print(f'888 = {binarySearch(0, len(arr)-1, 888)}')

이진 검색

정렬된 데이터를 기준으로 특정 값이나 범위를 검색하는데 사용

이진 검색을 활요한 심화 키워드 - Lower Bound, Upper Bound

• 정렬된 배열에서 특정 값 이상 또는 이하가 처음으로 나타나는 위치를 찾는 알고리즘

• 특정 데이터의 범위 검색 등에서 활용