재귀의 핵심 : 특정 시점으로 돌아간다!
재귀 함수 구하기
'''
백트래킹
완전탐색 + 가지치기 완전탐색은 재귀를 활용
가능성이 없는(볼 필요가 없는) 경우의 수를 제거하는 방법
중복된 순열
1~3 까지 숫자 배열이 있을 때
111, 112, 113, 121,,,,,,,332, 333
재귀는 특점 시점으로 돌아오는게 핵심~!!!
파라미터는 바로 작성하지 않고
구조를 먼저 잡고, 구조에서 필요한 함수를 전역변수/변수로 활용
'''
arr = [i for i in range(1, 4)]
path = [0] * 3 # 뭘 선택했는지에 대한 정보 담기
def dfs(level):
# 기저조건
# 이 문제에서는 3개를 뽑았을 때 까지 반복
if level == 3: # level 이 3개가 되면 종료
print(*path)
return
# 들어가기 전
# 다음 재귀 호출
# - 다음에 갈 수 있는 곳들은 어디인가?
# - 이 문제에서는 1, 2, 3 세 가지(arr의 길이 만큼) 경우의 수가 존재
# 기본 코드
# path[level] = 1
# dfs(level + 1)
#
# path[level] = 2
# dfs(level + 1)
#
# path[level] = 3
# dfs(level + 1)
# for 문 활용
for i in range(len(arr)):
path[level] = arr[i]
dfs(level+1)
# 갔다 와서 할 로직
dfs(0)순열
arr = [i for i in range(1, 4)]
path = [0] * 3 # 뭘 선택했는지에 대한 정보 담기
# 순열
# 123, 132, 213, 231, 312, 321
# 조건 : 숫자는 한 번만 사용해라!
def dfs(level):
if level == 3: # level 이 3개가 되면 종료
print(*path)
return
# 갈 수 있는 전체 후보군
for i in range(len(arr)):
# 여기는 못가!! (가지치기)
# 백트래킹 코드 팁
# 갈 수 없는 경우를 활용
# 아래 코드처럼 갈 수 없을 때 Continue
# if arr[i] not in path:
# path[level] = arr[i]
# dfs(level+1)
if arr[i] in path:
continue
path[level] = arr[i]
dfs(level + 1)
# 갔다 와서 할 로직
# 기존 방문을 초기화 해주어야 함
path[level] = 0
dfs(0)-
완전 탐색 경우의 수 계산
-
가지치기 후 대략적인 감소 예측
기저조건, 가지치기 더 없는지 확인 필요!
백트래킹 개념
여러가지 선택지(옵션)들이 존재하는 상황에서 한가지를 선택한다.
선택이 이루어지면 새로운 선택지들의 집합이 생성된다.
이런 선택을 반복하면서 최종 상태에 도달한다.
- 올바른 선택을 계속 하면 목표 상태(goal state)에 도달한다.
당첨 리프 노드 찾기
루트에서 갈 수 있는 노드를 선택한다.
꽝 노드까지 도달하면 최근의 선택으로 되돌아가서 다시 시작한다.
더 이상의 선택지가 없다면 이전의 선택지로 돌아가서 다른 선택을 한다.
루트까지 돌아갔을 경우 더 이상 선택지가 없다면 찾는 답이 없다.
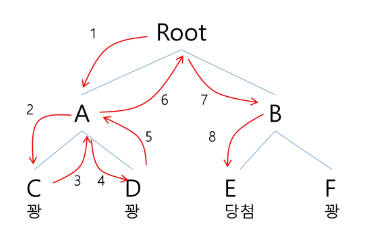
백트래킹과 깊이 우선 탐색과의 차이
어떤 노드에서 출발하는 경로가 해결책으로 이어질 것 같지 않으면 더 이상 그 경로를 따라가지 않음으로써 시도의 횟수를 줄임 (Prunning 가지치기)
깊이 우선 탐색이 모든 경로를 추격하는데 비해 백트래킹은 불필요한 경로를 조기에 차단
깊이 우선 탐색을 가하기에는 경우의 수가 너무 많음. 즉 N! 가지의 경우의 수를 가진 문제에 대해 깊이 우선 탐색을 가하면 당연히 처리 불가능한 문제
백트래킹 알고리즘을 적용하면 일반적으로 경우의 수가 줄어들지만 이 역시 최악의 경우에는 여전히 지수함수 시간 (Exponential Time)을 요하므로 처리 불가능

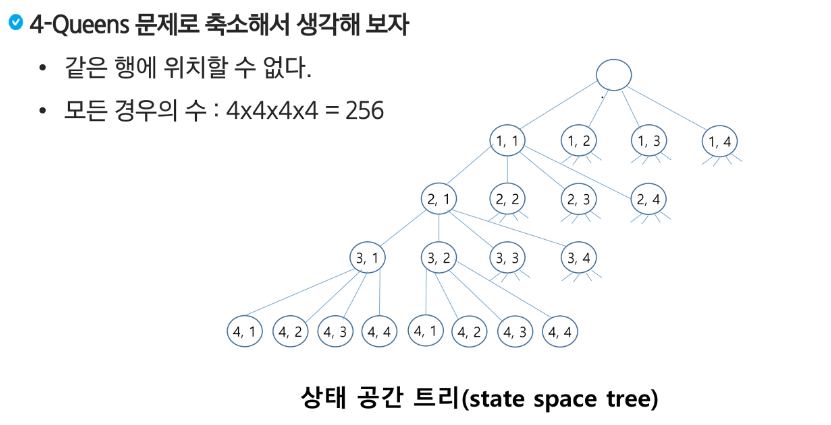
백트래킹 개념
루트 노드에서 리프 노드까지의 경로는 해답후보가 되는데, 깊이 우선 탐색을 하여 그 해답후보 중에서 답을 찾을 수 있다.
그러나 이 방법을 사용하면 해답이 될 가능성이 전혀 없는 노드의 후손 노드들도 모두 검색해야 하므로 비효율적이다.
모든 후보를 검사하지 않는다.
백트래킹 기법
어떤 노드의 유망성을 점검한 후에 유망하지 않다고 결정되면 그 노드의 부모로 되돌아가 다음 자식 노드로 감
어떤 노드를 방문하였을 때 그 노드를 포함한 경로가 해답이 될 수 없으면, 그 노드가 유망하지 않다고 하며 반대로 해답의 가능성이 있으면 유망하다고 한다.
가지치기(Prunning) : 유망하지 않은 노드가 포함되는 경로는 더 이상 고려하지 않는다.
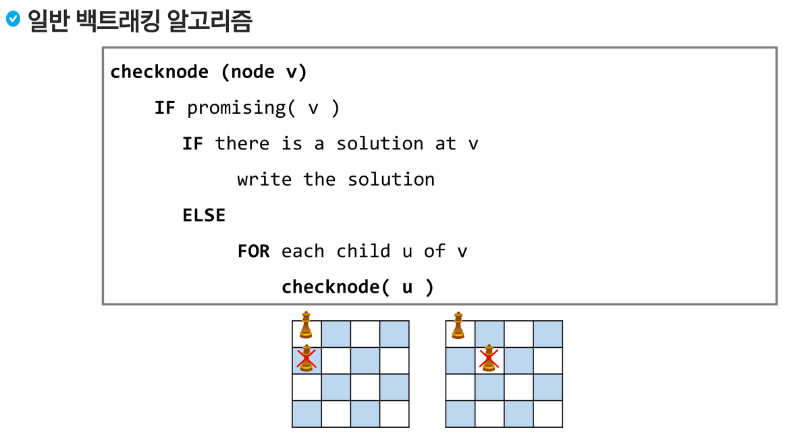
백트래킹을 이용한 알고리즘의 절차
-
상태 공간 트리의 깊이 우선 검색을 실시한다.
-
각 노드가 유망한지를 점검한다.
-
만일 그 노드가 유망하지 않다면, 그 노드의 부모 노드로 돌아가서 검색을 계속한다.
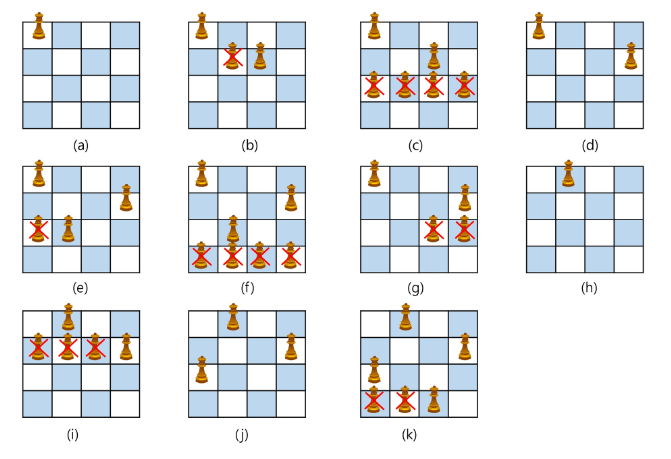
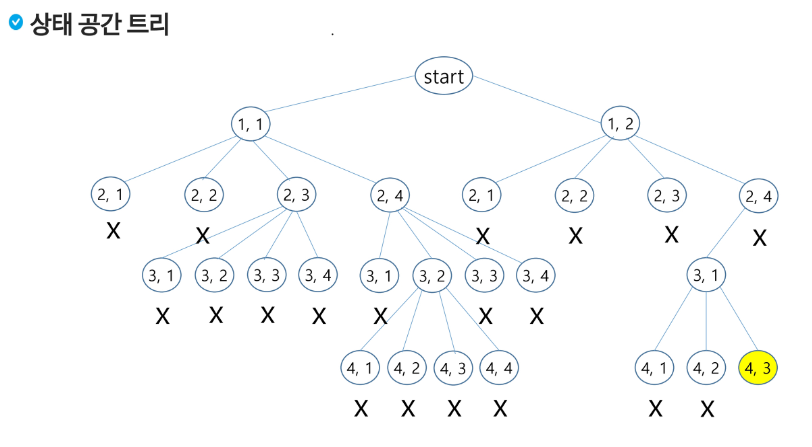

상태 공간 트리를 구축하여 문제를 해결


dfs(sum): # 종료 조건 확인
if sum == 10:
return
if sum > 10: # 기저조건에서 가지치기
return트리 개요
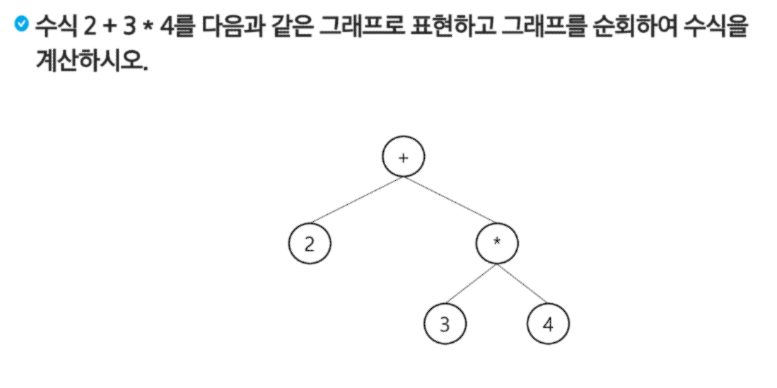
싸이클이 없는 무향 연결 그래프
- 싸이클
- 방문했던 노드로 다시 돌아오는 다른 경로가 있는 경우
- 무향
- 간선에 방향이 없다 (양방향)
- 연결 그래프
- 모든 꼭지점이 서로 갈 수 있는 경로가 있다.
위의 세 조건을 모두 만족해야 트리가 생성된다.
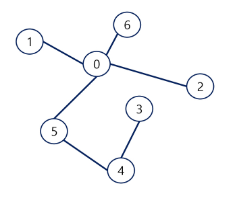
트리는 사이클이 없는 무향 연결 그래프이다.
두 노드(or 정점) 사이에는 유일한 경로가 존재한다.
각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
각 노드는 자식 노드가 없거나 하나 이상이 존재할 수 있다.
비 선형 구조
원소들 간에 1: n 관계를 가지는 자료구조
원소들 간에 계층관계를 가지는 계층형 자료구조
한 개 이상의 노드로 이루어진 유한 집합이며 다음 조건을 만족한다.
-
노드 중 부모가 없는 노드를 루트(root)라 한다.
-
나머지 노드들은 n(>=0) 개의 분리 집합 T1, ..., TN 으로 분리될 수 있다.
이들 T1, ..., TN 은 각각 하나의 트리가 되며 (재귀적 정의) 루트의 서브트리(subtree)라 한다.
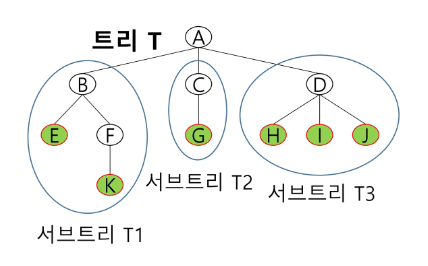
노드 (node) : 트리의 원소이고 정점(vertex)라고도 한다.
- 트리 T의 노드 : A, B, C, D, E, F, G, H..
간선 (edge) : 노드를 연결하는 선
- 부모 노드와 자식 노드를 연결
루트 노드 (root node) : 트리의 시작 노드
-
트리 T의 루트 노드 - A
-
형제 노드 끼리는 연결되지 않음 → 사이클 생성을 방지하기 위해
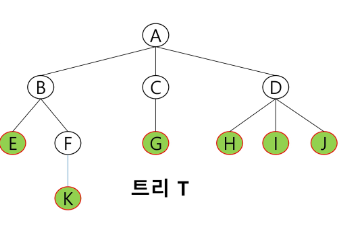
형제 노드 : 같은 부모 노드의 자식 노드들
조상 노드 : 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들
서브 트리 : 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
자손 노드 : 서브 트리에 있는 하위 레벨의 노드들
차수(degree)
노드의 차수 : 노드에 연결된 자식 노드의 수
- B의 차수 = 2, C의 차수 = 1
트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값
단말 노드 (리프 노드) : 차수가 0인 노드, 자식 노드가 없는 노드
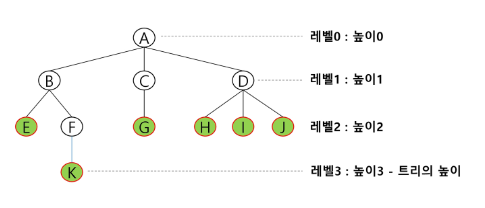
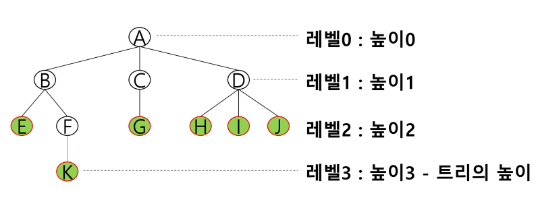
높이
노드의 높이 : 루트에서 노드에 이르는 간선의 수, 노드의 레벨
트리의 높이 : 트리에 있는 노드의 높이 중에서 가장 큰 값. 최대 레벨
이진 트리
이진 트리(binary tree)
모든 노드들이 최대 2개의 서브 트리를 갖는 특별한 형태의 트리
각 노드가 자식 노드를 최대 2개까지만 가질 수 있는 트리
-
왼쪽 자식 노드
-
오른쪽 자식 노드
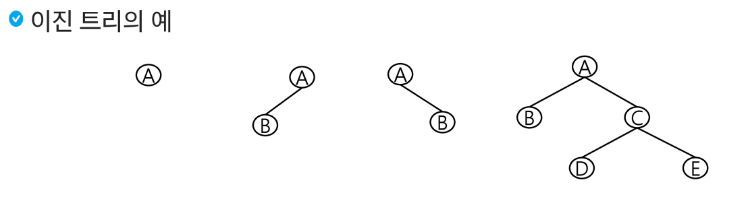

포화 이진 트리
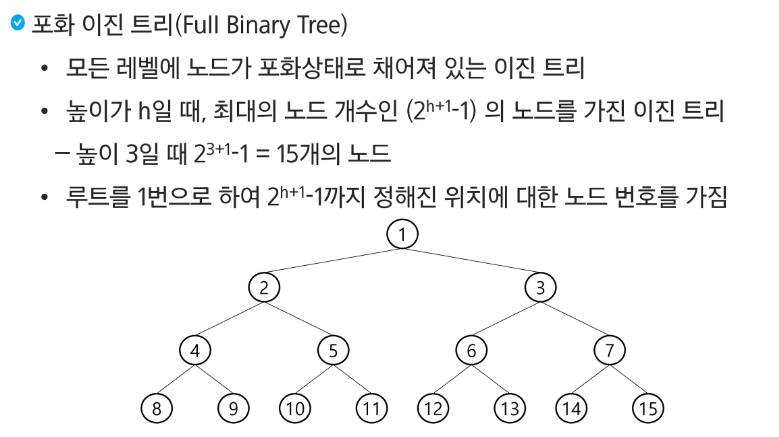
완전 이진 트리
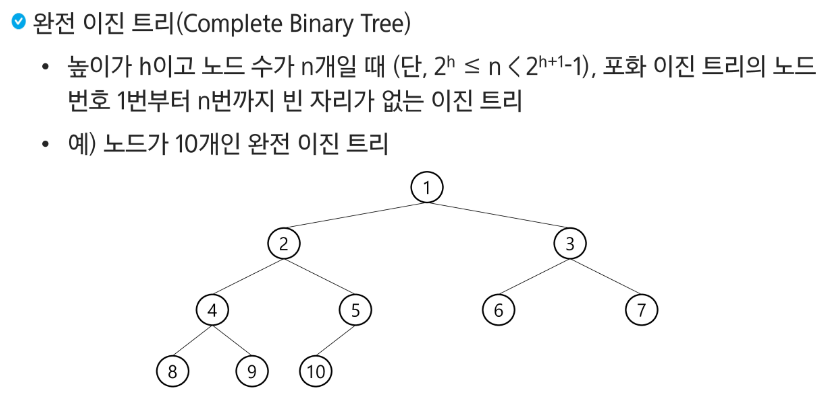
편향 이진 트리
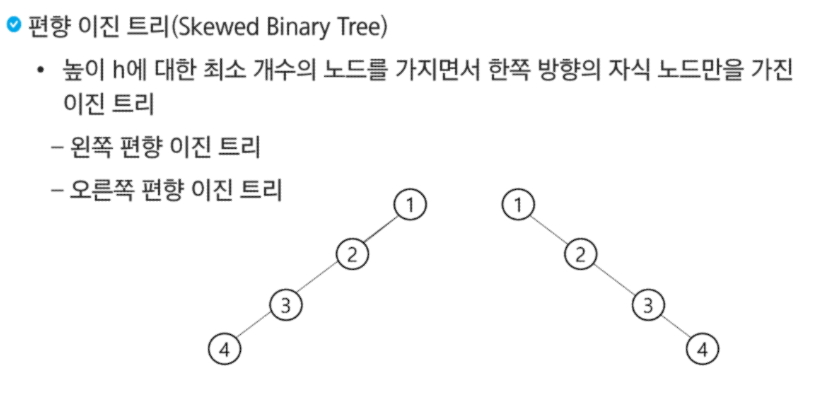
순회
순회
순회란 트리의 각 노드를 중복되지 않게 전부 방문하는 것을 말하는데 트리는 비 선형 구조이기 때문에 선형구조에서와 같이 선후 연결 관계를 알 수 없다.


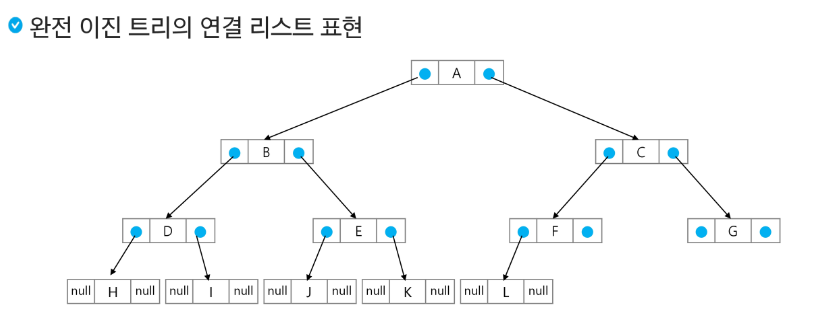
개발용 트리
arr = [1, 2, 1, 3, 2, 4, 3, 5, 3, 6, 4, 7, 5, 8, 5, 9, 6, 10, 6, 11, 7, 12, 11, 13]
# 정석 개발 버전
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def insert(self, child):
# 왼쪽에 삽입 시도
if not self.left:
self.left = child
return
# 오른쪽에 삽입 시도
if not self.right:
self.right = child
return
# 삽입 실패
return
def inorder(self):
if self != None: # 자식이 아무것도 없으면
# 왼쪽이 있으면 계속 탐색
if self.left:
self.left.inorder()
if self.right:
self.right.inorder()
print(self.value, end=' ')
# 이진 트리 만들기
# 1. 노드들을 생성
nodes = [TreeNode(i) for i in range(0, 14)]
# 2. 간선을 연결
for i in range(0, len(arr), 2):
parent_node = arr[i]
child_node = arr[i+1]
nodes[parent_node].insert(nodes[child_node])
nodes[1].inorder()
실제 활용 트리 코드
arr = [1, 2, 1, 3, 2, 4, 3, 5, 3, 6, 4, 7, 5, 8, 5, 9, 6, 10, 6, 11, 7, 12, 11, 13]
# 코딩테스트에서는 간단하게
nodes= [[] for _ in range(14)]
for i in range(0, len(arr), 2):
parent_node = arr[i]
child_node = arr[i+1]
nodes[parent_node].append(child_node)
# 자식이 없다는 걸 표시하기 위해서 None
for li in nodes:
for _ in range(len(li), 2):
li.append(None)
# 중위순회 구현
def inorder(nodeNum):
if nodeNum == None:
return
# 왼쪽으로 갈 수 있다면 진행
inorder(nodes[nodeNum][0])
print(nodeNum, end = ' ')
# 오른쪽으로 갈 수 있다면 진행
inorder(nodes[nodeNum][1])
inorder(1)
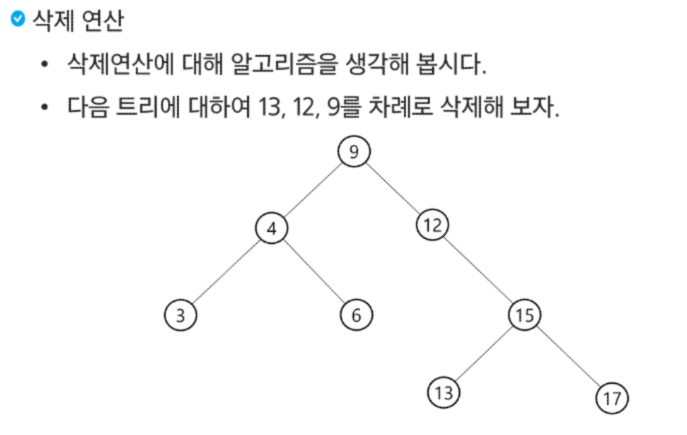
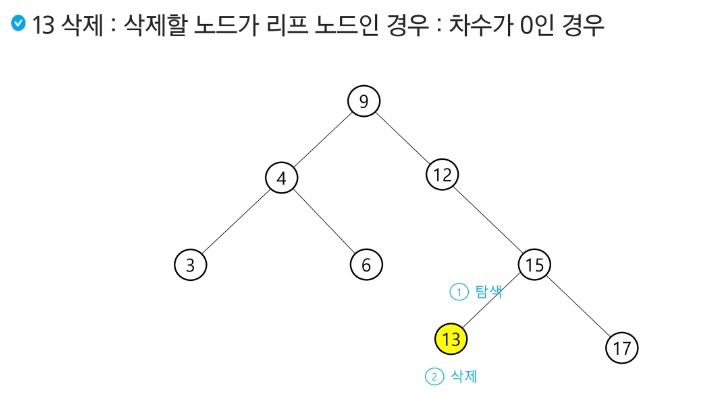
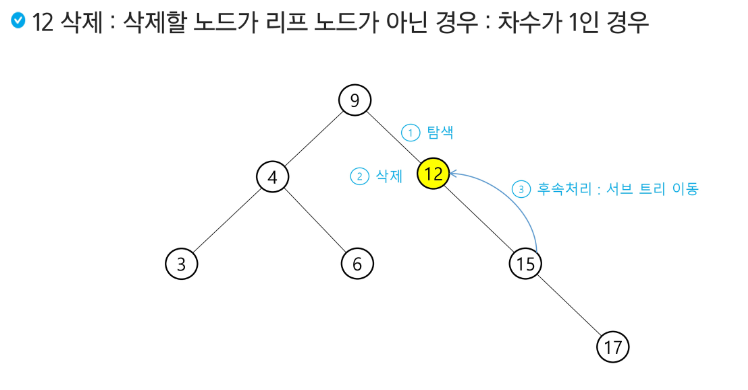
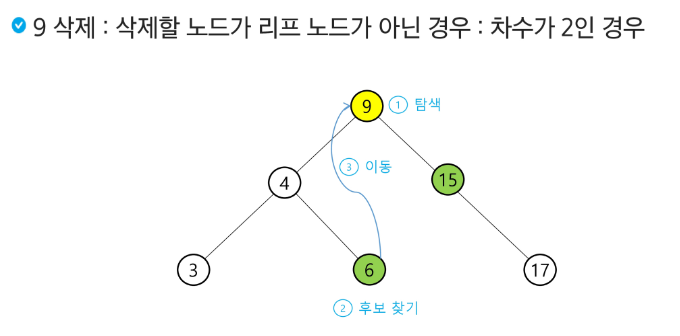
이진탐색트리(BST)
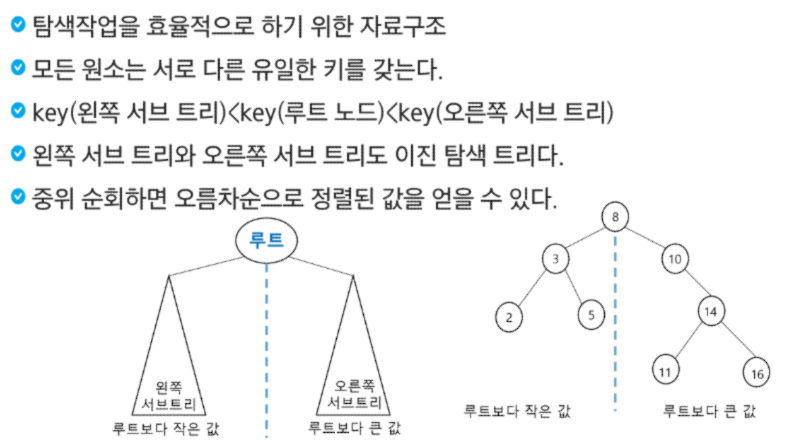

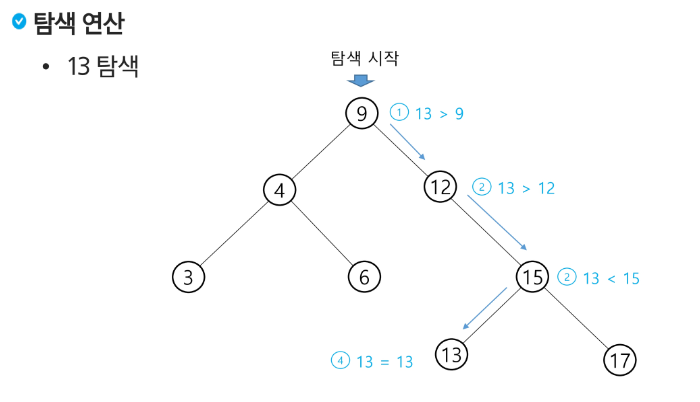
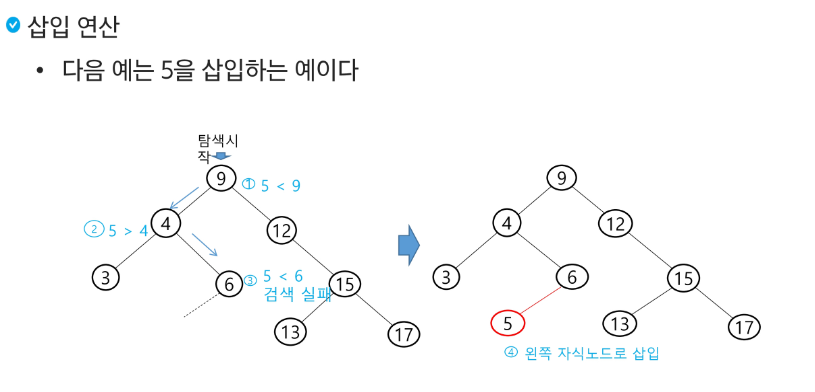
탐색 연산의 횟수는 트리의 높이만큼이다!


힙트리(Heap Tree)
힙(heap)
완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 자료 구조
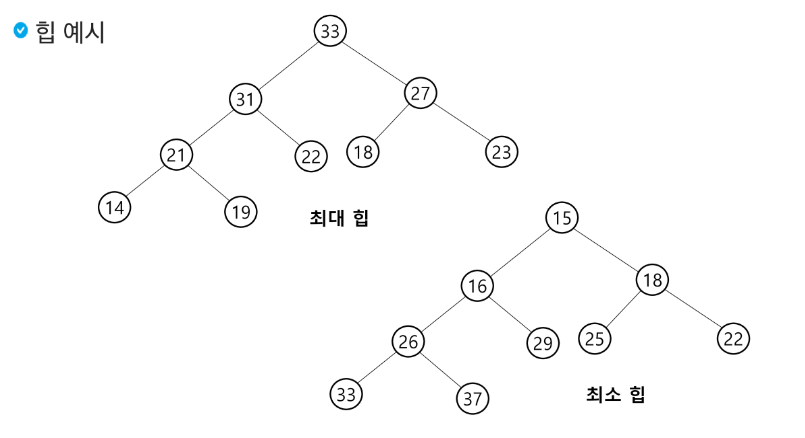
최대 힙
키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
부모 노드의 키 값 > 자식 노드의 키 값
루트 노드 : 키 값이 가장 작은 노드
최소 힙
키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
부모 노드의 키 값 < 자식 노드의 키 값
루트 노드 : 키 값이 가장 작은 노드
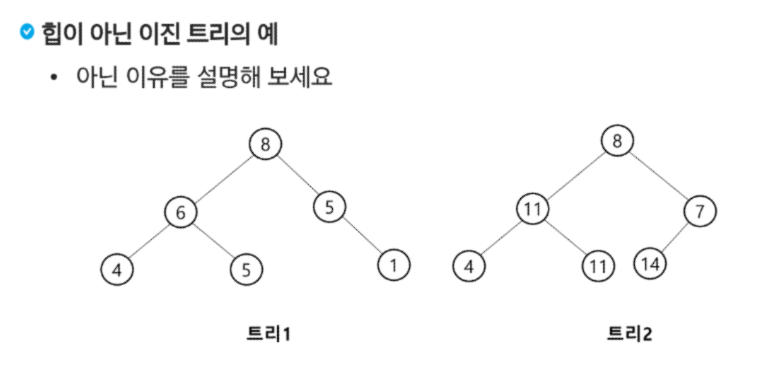
완전 이진 트리가 아니어서!
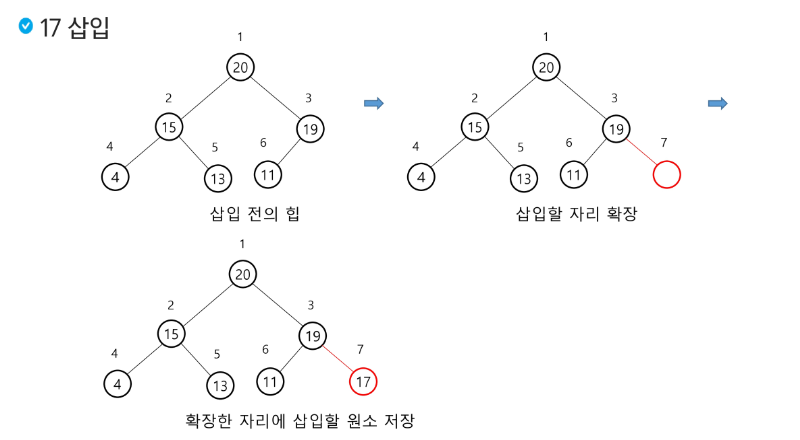
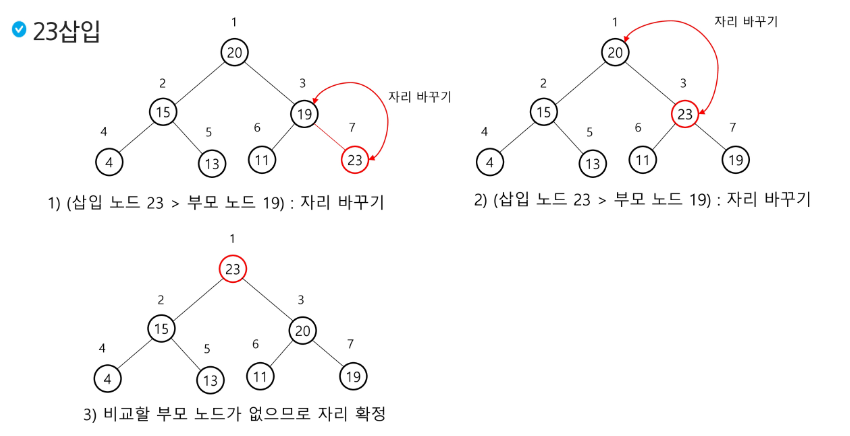
우선 값을 삽입하고, 주위 값들과 비교해가며 본인의 위치를 찾아간다!
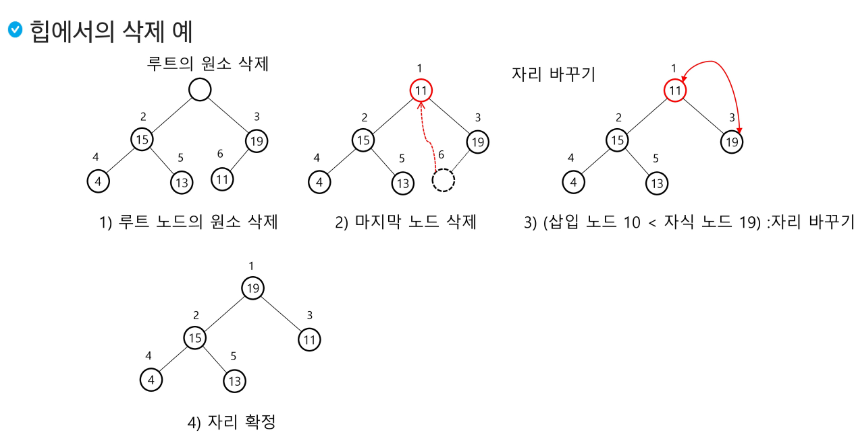
힙 연산 - 삭제
힙에서는 루트 노드의 원소만을 삭제할 수 있다.
루트 노드의 원소를 삭제하여 반환한다.
힙의 종류에 따라 최대값 또는 최소값을 구할 수 있다.
- 우선 순위 큐와 비교
힙의 활용
힙을 활용하는 대표적인 2가지 예는 특별한 큐의 구현과 정렬이다.
우선순위 큐를 구현하는 가장 효율적인 방법은 힙을 사용하는 것이다.
-
노드 하나의 추가/삭제가 시간 복잡도가 O(log N)이고 최대값/최소값을 O(1)에 구할 수 있다.
-
완전 정렬보다 관리 비용이 적다.
배열을 통해 트리 형태를 쉽게 구현할 수 있다.
-
부모나 자식 노드를 O(1)연산으로 쉽게 찾을 수 있다.
-
n 위치에 있는 노드의 자식은 2n 과 2n+1 위치한다.
-
완전 이진 트리의 특성에 의해 추가/삭제의 위치는 자료의 시작과 끝을 인덱스로 쉽게 판단할 수 있다.
힙 정렬은 힙 자료구조를 이용해서 이진 탐색과 유사한 방법으로 수행된다.
정렬을 위한 2단계
-
하나의 값을 힙에 삽입한다. (반복)
-
힙에서 순차적(오름차순) 으로 값을 하나씩 제거한다.
힙 정렬의 시간복잡도
-
N개의 노드 삽입 연산 + N 개의 노드 삭제 연산
-
삽입과 삭제 연산은 각각 O(log N)이다.
-
따라서 전체 정렬은 O(Nlog N)이다.
힙 정렬은 배열에 저장된 자료를 정렬하기에 유용하다.
