계산기 1
문자열로 된 계산식이 주어질 때, 스택을 이용하여 이 계산식의 값을 계산할 수 있다.
문자열 수식 계산의 일반적인 방법
step1. 중위 표시법의 수식을 후위 표기법으로 변경한다. (스택 이용)
-
중위표기법(infix notation)
연산자를 피연산자의 한 가운데 표기하는 방법
ex ) A+B
-
후위표기법 (postfix notation)
연산자를 피연산자 뒤에 표기하는 방법
ex ) AB+
step2. 후위 표기법의 수식을 스택을 이용하여 계산한다.
step1. 중위 표기식의 후위표기식 변환 방법 1
-
수식의 각 연산자에 대해서 우선순위에 따라 괄호를 사용하여 다시 표현한다.
-
각 연산자를 그에 대응하는 오른쪽 괄호의 뒤로 이동시킨다.
-
괄호를 제거한다.

step1. 중위 표기법에서 후위 표기법으로의 변환 알고리즘(스택 이용)2
-
입력받은 중위표기식에서 토큰을 읽는다.
-
토큰이 피연산자이면 토큰을 출력한다.
-
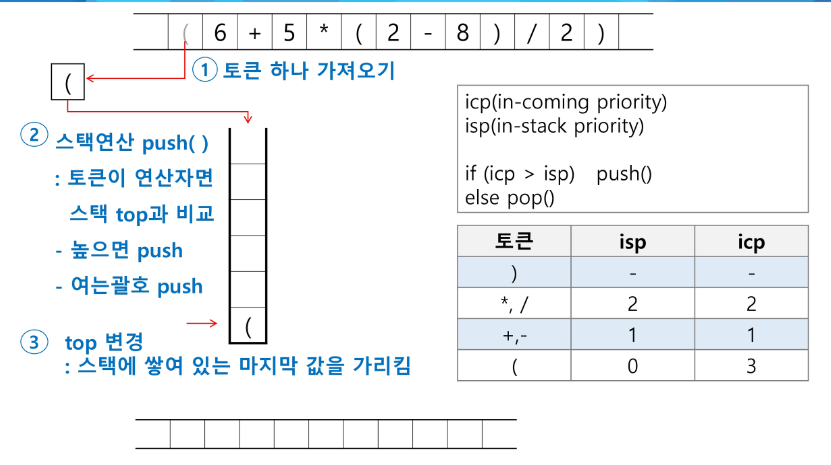
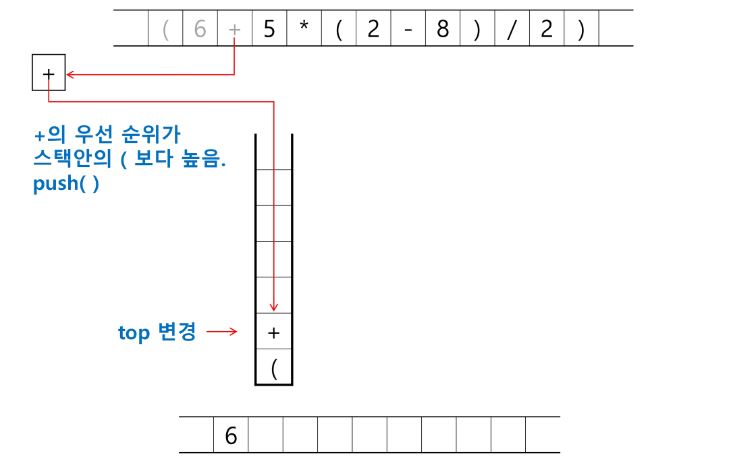
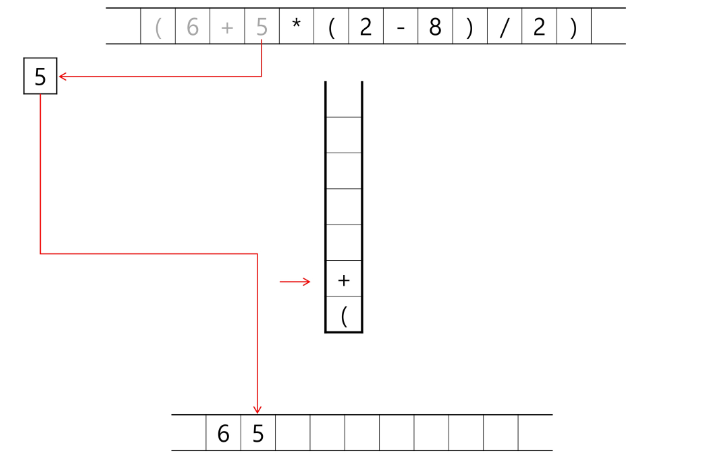
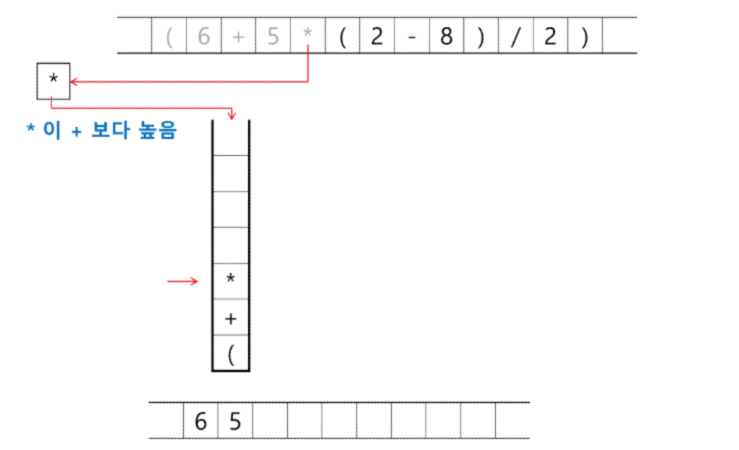
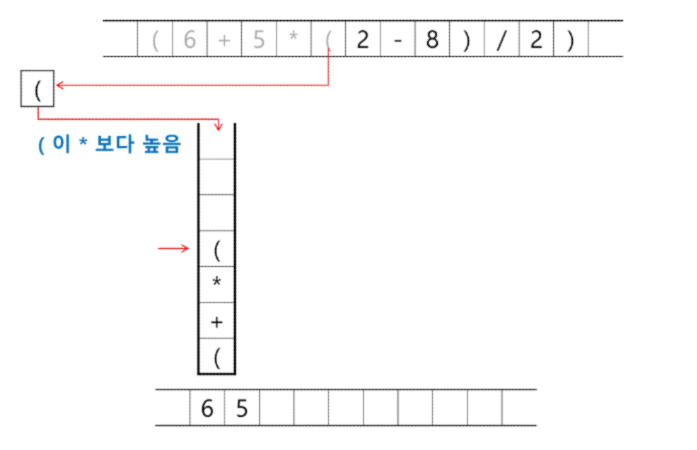
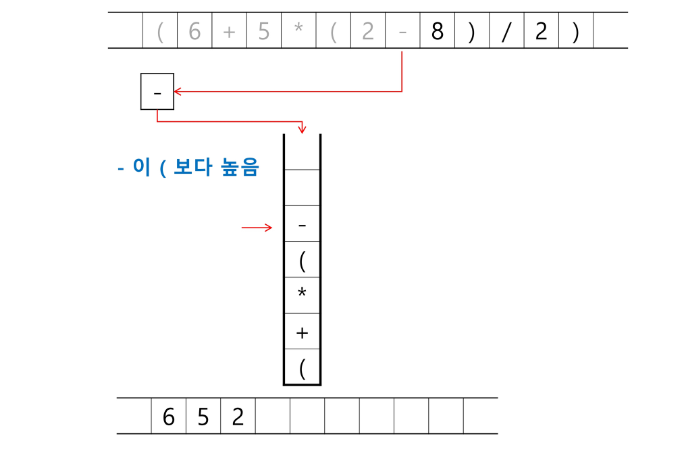
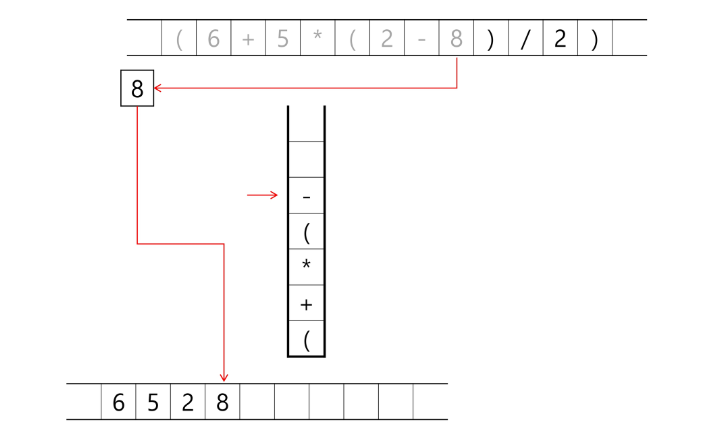
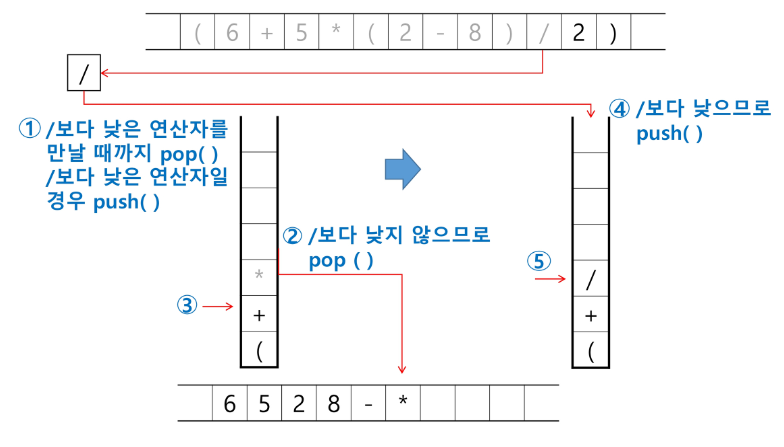
토큰이 연산자(괄호포함)일 때, 이 토큰이 스택의 top에 저장되어있는 연산자보다 우선순위가 높으면 스택에 push 하고, 그렇지 않으면 스택 top의 연산자의 우선순위가 토큰의 우선순위보다 작을 때 까지 스택에서 pop 한 후 토큰의 연산자를 push 한다. 만약 top에 연산자가 없으면 push한다.
-
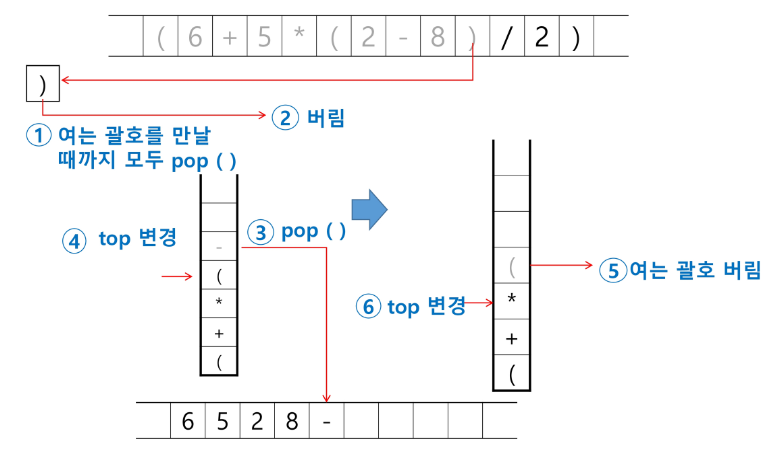
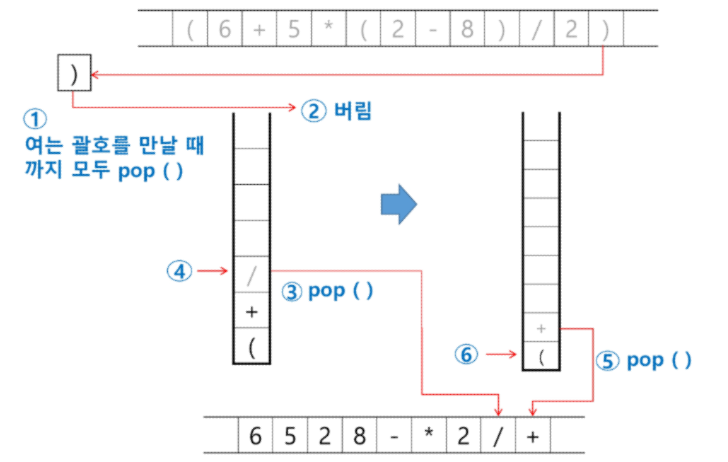
토큰이 오른쪽 괄호')' 이면 스택의 왼쪽 괄호'('가 나올때까지 스택에 pop연산을 수행하고 pop한 연산자를 출력한다. 왼쪽 괄호를 만나면 pop만 하고 출력하지는 않는다.
-
중위 표기식에 더 읽을 것이 없다면 중지하고, 더 읽을 것이 있다면 1부터 다시 반복한다.
-
스택에 남아있는 연산자를 모두 pop하여 출력한다.
- 스택 밖의 왼쪽 괄호는 우선순위가 가장 높으며, 스택 안의 왼쪽 괄호는 우선순위가 가장 낮다.

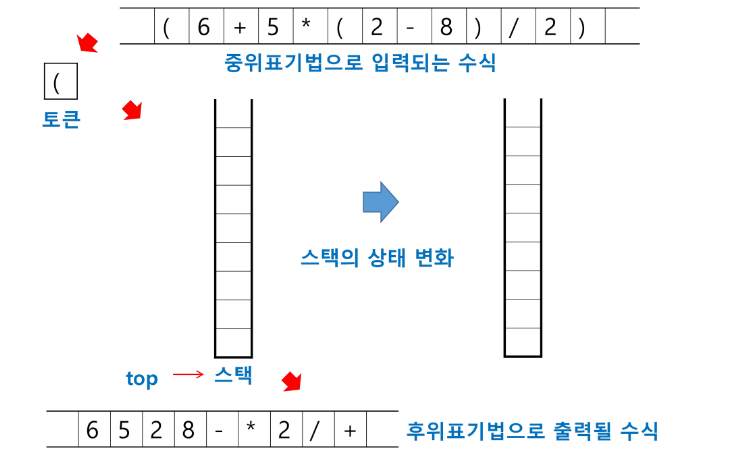




계산기2
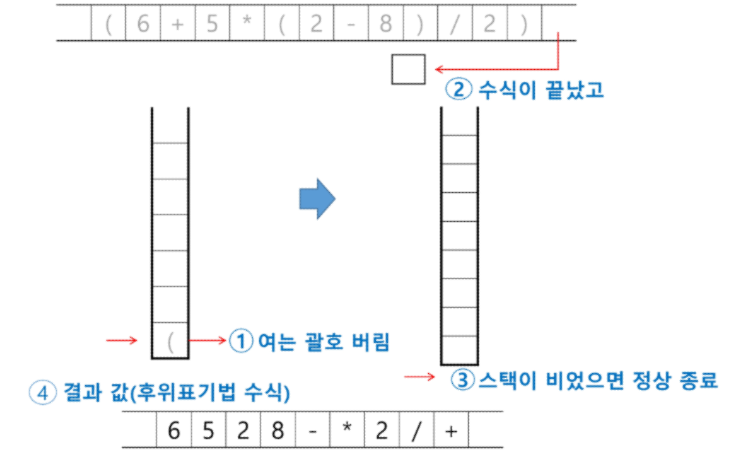
step2. 후위 표기법의 수식을 스택을 이용하여 계산
-
피연산자를 만나면 스택에 push 한다.
-
연산자를 만나면 필요한 만큼의 피연산자를 스택에서 pop 하여 연산하고, 연산 결과를 다시 스택에 push 한다.
-
수식이 끝나면, 마지막으로 스택을 pop 하여 출력한다.
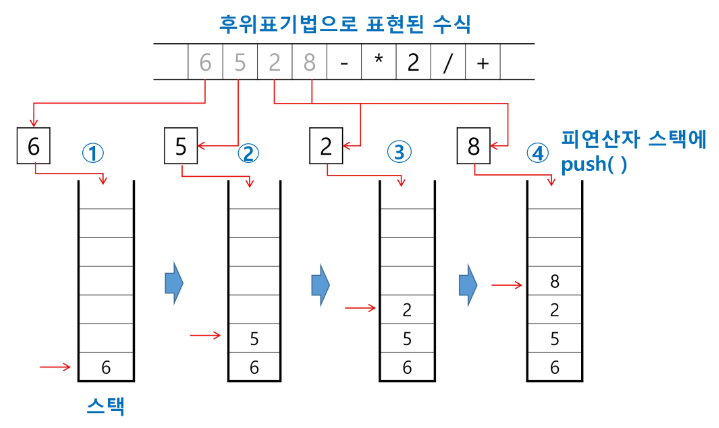
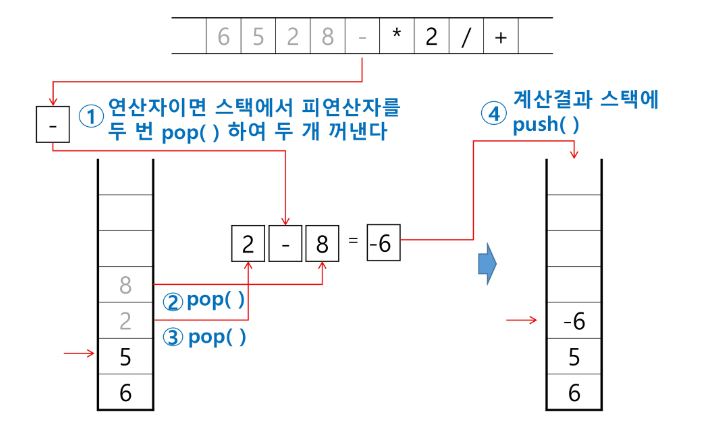
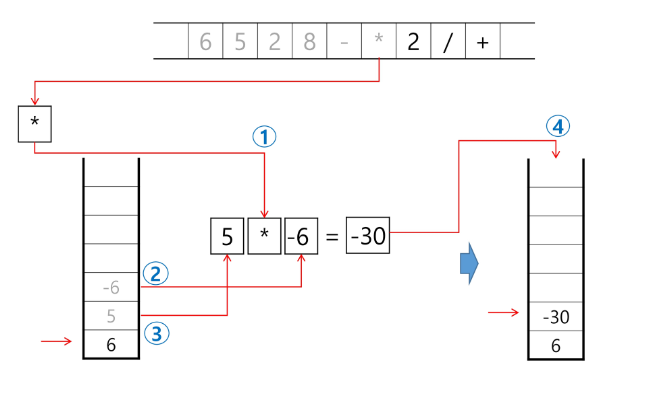
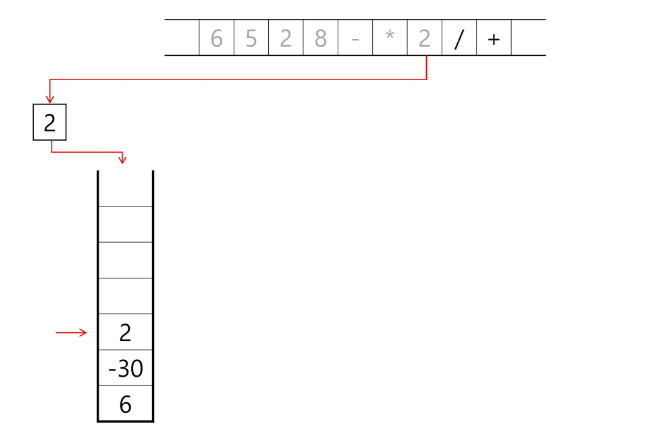
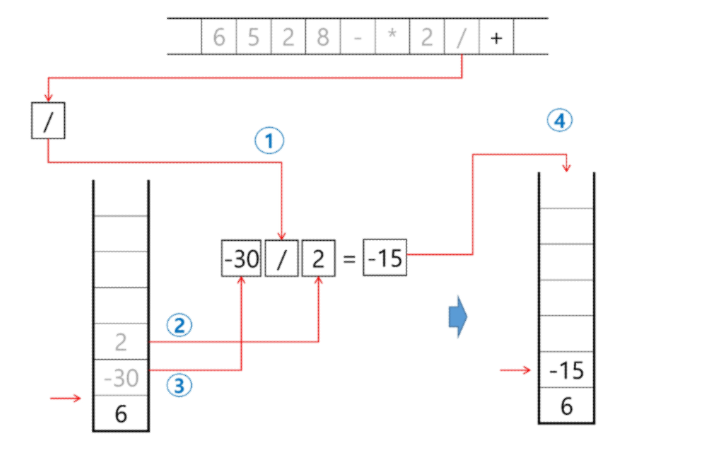
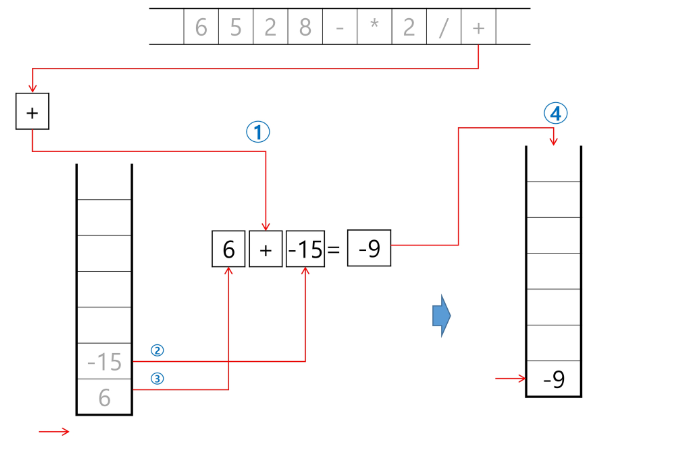
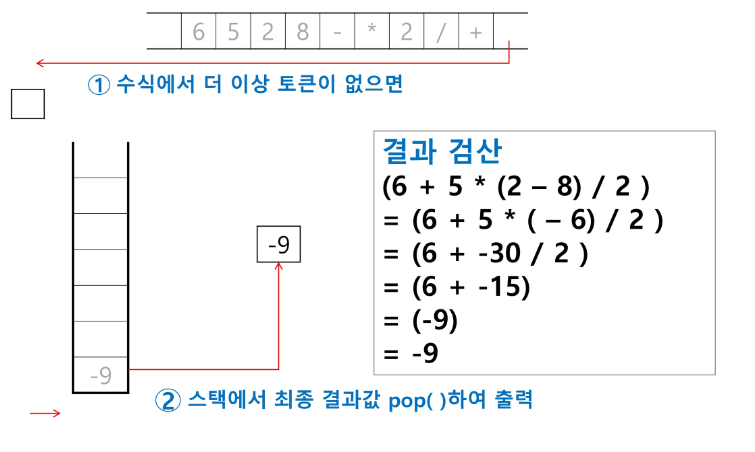
계산기 내부에서 어떠한 과정을 통해 해당 값이 나오는지 알 수 있음
'''
fx = (6+5*(2-8)/2)
'''
top = -1
stack = [0] * 100 #넉넉하게 제작
icp = {'(':3, '*':2, '/' : 2, '+' : 1, '-': 1} # 스택 밖에서의 우선순위
isp = {'(':0, '*':2, '/' : 2, '+' : 1, '-': 1} # 스택 안에서의 우선순위
fx = '(6+5*(2-8)/2)'
postfix =''
for tk in fx:
# 여는 괄호 push, 연산자이고 top 원소보다 우선순위가 높으면 push
if tk == '(' or (tk in '*/+-' and isp[stack[top]] < icp[tk]):
top += 1 #push
stack[top] = tk # append top을 해도 무관
elif tk in '*/+-' and isp[stack[top]] >= icp[tk] : # 연산자이고 top원소보다 우선순위가 높지 않으면
while isp[stack[top]] >= icp[tk] : # top원소보다 우선순위가 낮을 때 까지 pop
top -= 1 # pop
postfix += stack[top+1]
top += 1 #push
stack[top] = tk
elif tk == ')': # 닫는 괄호면, 여는 괄호를 만날때까지 pop
while stack[top] != '(':
top -=1 #pop
postfix += stack[top+1]
top -= 1 # 여는 괄호 pop 해서 버림
stack[top+ 1]
else: # 피연산자인 경우
postfix += tk
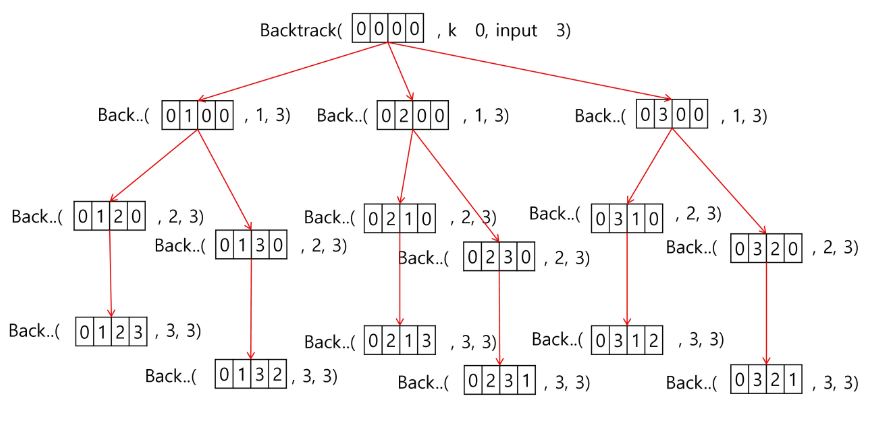
print(postfix)백트래킹
백트래킹
백트래킹 (Backtracking) 기법은 해를 찾는 도중에 막히면 (즉, 해가 아니면) 되돌아가서 다시 해를 찾아가는 기법이다.
백트래킹 기법은 최적화(optimization)문제와 결정 (decision)문제를 해결할 수 있다.
결정 문제 : 문제의 조건을 만족하는 해가 존재하는지 여부를 'yes' 또는 'no'가 답하는 문제
-
미로찾기
-
n-Queen 문제
-
Map coloring
-
부분집합의 합(Subset Sum)문제 등
미로 찾기
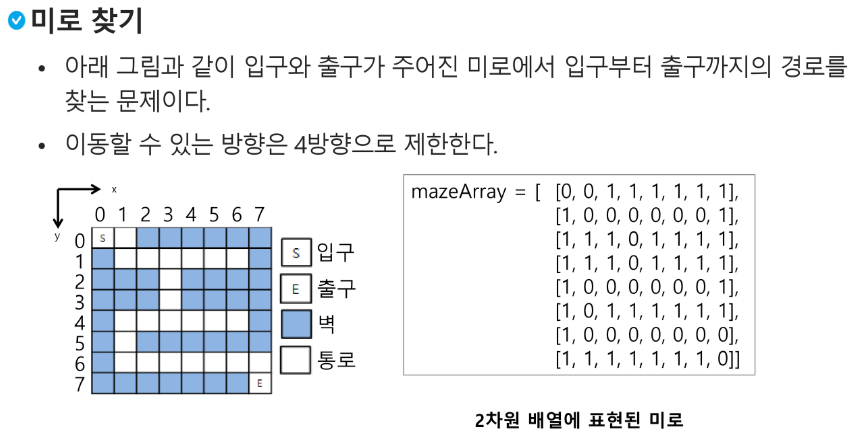
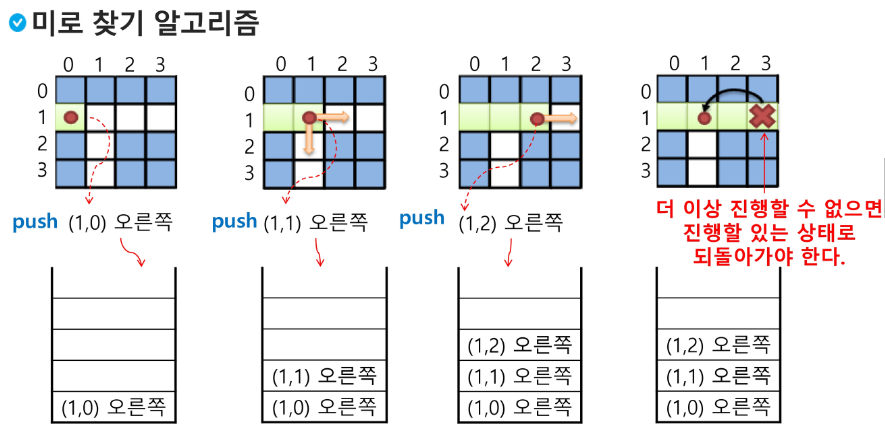
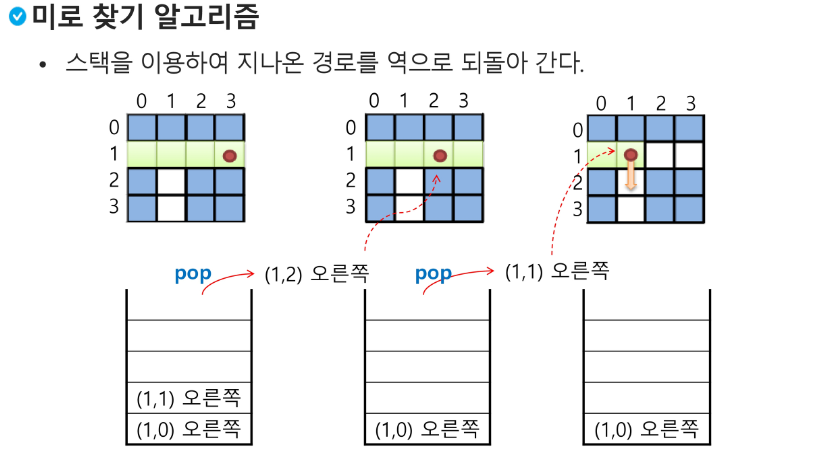
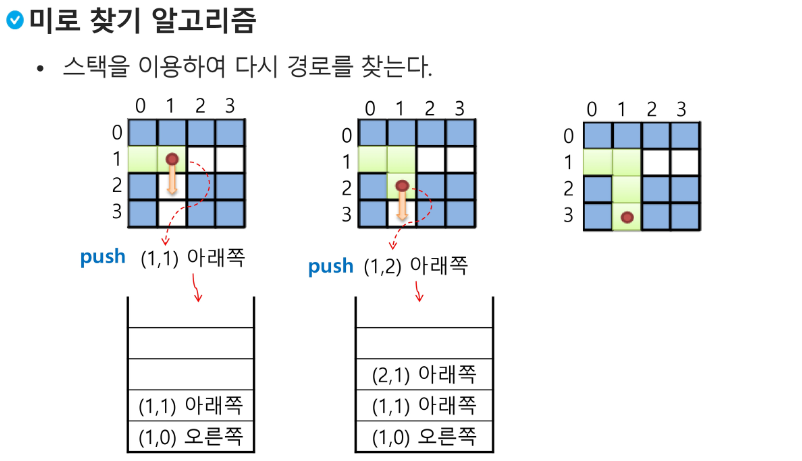
백트래킹과 깊이우선탐색과의 차이
-
어떤 노드에서 출발하는 경로가 해결책으로 이어질 것 같지 않으면 더 이상 그 경로를 따라가지 않음으로써 시도의 횟수를 줄임 (Prunning 가지치기)
-
깊이 우선 탐색이 모든 경로를 추적하는데 비해 백트래킹은 불필요한 경로를 조기에 차단
-
깊이우선탐색을 가하기에는 경우의 수가 너무 많음. 즉 N! 가지의 경우의 수를 가진 문제에 대해 깊이우선탐색을 가하면 당연히 처리 불가능한 문제
-
백트래킹 알고리즘을 적용하면 일반적으로 경우의 수가 줄어들지만 이 역시 최악의 경우에는 여전히 지수함수 시간(Exponential Time)을 요하므로 처리 불가능
모든 후보를 검사?
NO!
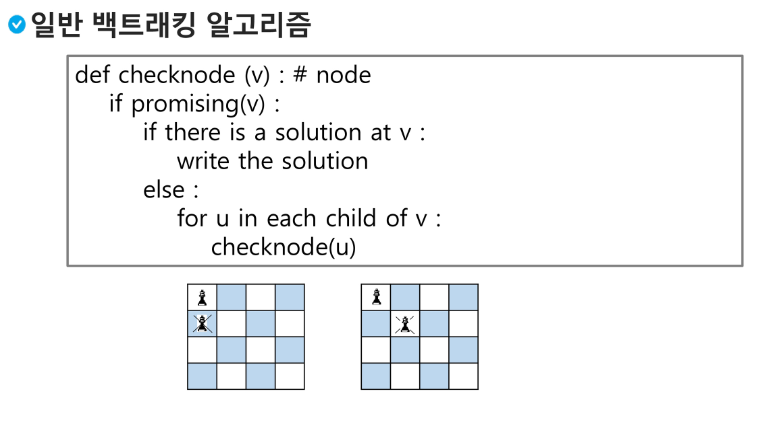
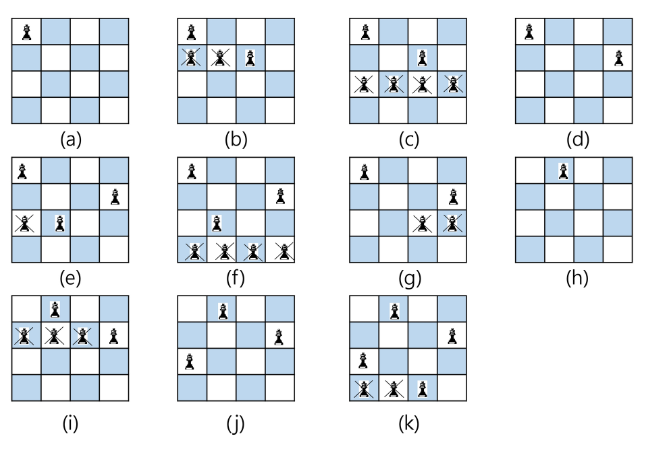
백트래킹 기법
-
어떤 노드의 유망성을 점검한 후에 유망(promising)하지 않다고 결정되면 그 노드의 부모로 되돌아가(backtracking) 다음 자식 노드로 감
-
어떤 노드를 방문하였을 때, 그 노드를 포함한 경로가 해답이 될 수 없으면 그 노드를 유망하지 않다고 하며, 반대로 해답의 가능성이 있으면 유망하다고 한다.
-
가지치기 (pruning) : 유망하지 않은 노드가 포함되는 경로는 더 이상 고려하지 않는다.
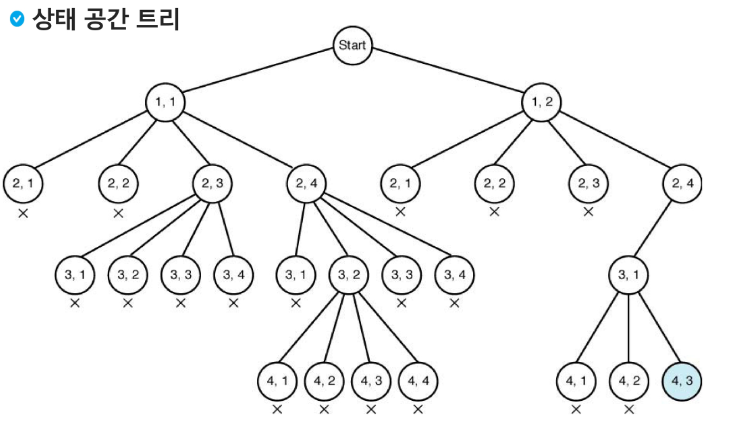
백트래킹을 이용한 알고리즘은 다음과 같은 절차로 진행된다.
-
상태 공간 트리의 깊이 우선 검색을 실시한다.
-
각 노드가 유망한지를 점검한다.
-
만일 그 노드가 유망하지 않으면, 그 노드의 부모 노드로 돌아가서 검색을 계속한다.

부분집합
부분집합
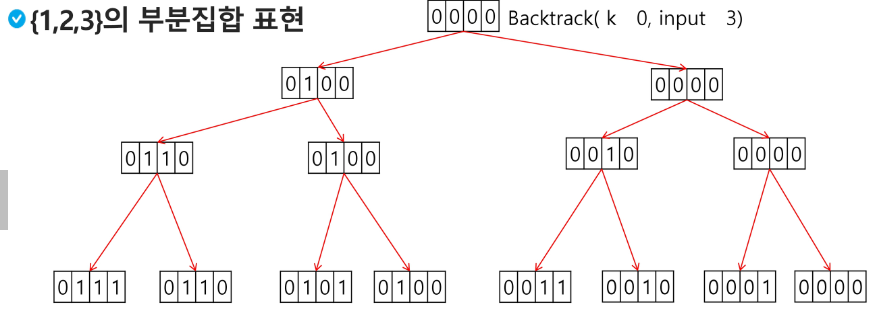
어떤 집합의 공집합과 자기자신을 포함한 모든 부분집합을 powerset이라고 하며 구하고자 하는 어떤 집합의 원소 개수가 n일 경우 부분집합의 개수는 2^n 개 이다.
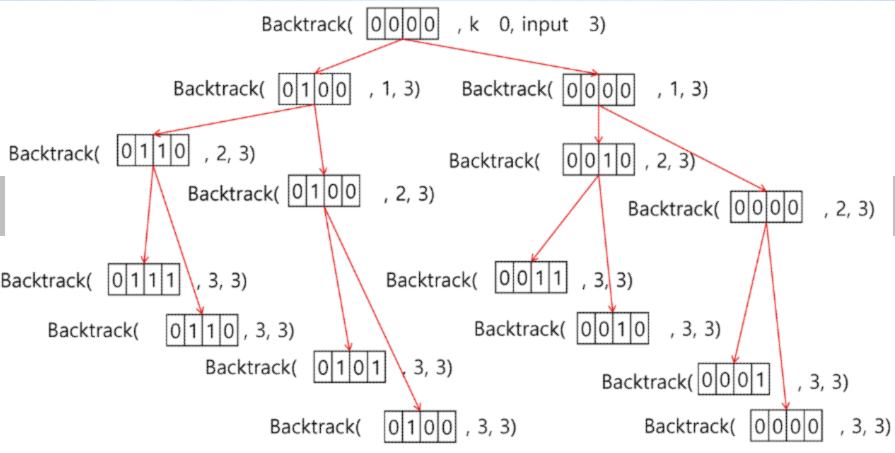
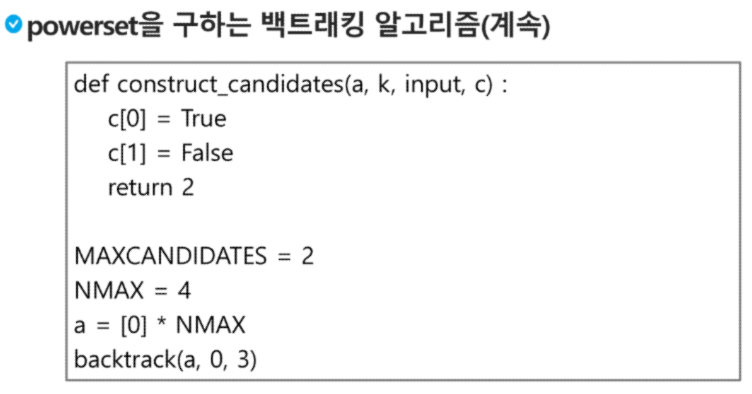
백트래킹 기법으로 powerset 을 만들어보자
-
앞에서 설명한 일반적인 백트래킹 접근 방법을 이용한다.
-
n개의 원소가 들어있는 집합의 2^n 개의 부분집합을 만들 때는, true 또는 false 값을 가지는 항목들로 구성된 n개의 배열을 만드는 방법을 이용
-
여기서 배열의 i 번째 항목은 i 번째의 원소가 부분집합의 값인지 아닌지를 나타내는 값이다.


bit = [0, 0, 0, 0]
for i in range(2):
bit[0] = i
for j in range(2):
bit[1] = j
for k in range(2):
bit[2] = k
for l in range(2):
bit[3] = l
print(bit)def f(i, k):
if i == k:
for j in range(k):
if bit[j] :
print(arr[j], end = ' ')
print()
else:
for j in range(2):
bit[i] = j
f(i+1, k)
N = 4
arr = [1, 2, 3, 4]
bit = [0] * N # bit[i] : arr[i] 가 부분집합에 포함되어있는지를 나타내는 배열
f(0, N) # bit[i] 에 1 또는 0을 채우고, N 개의 원소가 결정되면 부분집합을 출력def f(i, k):
if i == k:
for j in range(k):
if bit[j] :
print(arr[j], end = ' ')
print()
else:
# for j in range(2):
# bit[i] = j
# f(i+1, k)
bit[i] = 1
f(i+1, k)
bit[i] = 0
f(i+1, k)
N = 4
arr = [1, 2, 3, 4]
bit = [0] * N # bit[i] : arr[i] 가 부분집합에 포함되어있는지를 나타내는 배열
f(0, N) # bit[i] 에 1 또는 0을 채우고, N 개의 원소가 결정되면 부분집합을 출력순열