부분집합/순열

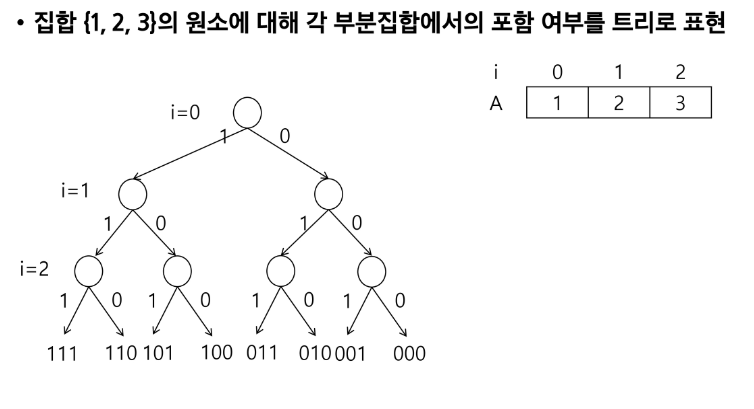
부분집합을 포함시켰는지 여부를 확인
def f(i, k):
if i == k: # 모든 원소에 대해 결정하면
ss = 0 # 부분집합 원소의 합
for j in range(k):
if bit[j]: # A[i]가 포함된 경우
print(A[j], end = ' ')
ss += A[j]
print(ss)
else:
for j in range(1, -1, -1):
bit[i] = j
f(i+1, k)
# bit[i] = 1
# f(i+1, k)
# bit[i] = 0
# f(i+1, k)
N = 3
A = [1, 2, 3]
bit = [0] * N # bit[i]는 A[i]가 부분집합에 포함되는지 표시
f(0, N)def f(i, k, t): # k 개의 원소를 가진 배열A, 부분집합의 합이 t인 경우
if i == k: # 모든 원소에 대해 결정하면
ss = 0 # 부분집합 원소의 합
for j in range(k):
if bit[j]: # A[i]가 포함된 경우
ss += A[j] # 부분집합 원소의 합
#print(A[j], end = ' ') 부분집합 출력
if ss == t:
for j in range(k):
if bit[j]: # A[i]가 포함된 경우
ss += A[j]
print(A[j], end = ' ')
print() # 부분집합 출력
else:
for j in range(1, -1, -1):
bit[i] = j
f(i+1, k, t)
# bit[i] = 1
# f(i+1, k)
# bit[i] = 0
# f(i+1, k)
N = 10
A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
bit = [0] * N # bit[i]는 A[i]가 부분집합에 포함되는지 표시
f(0, N, 10)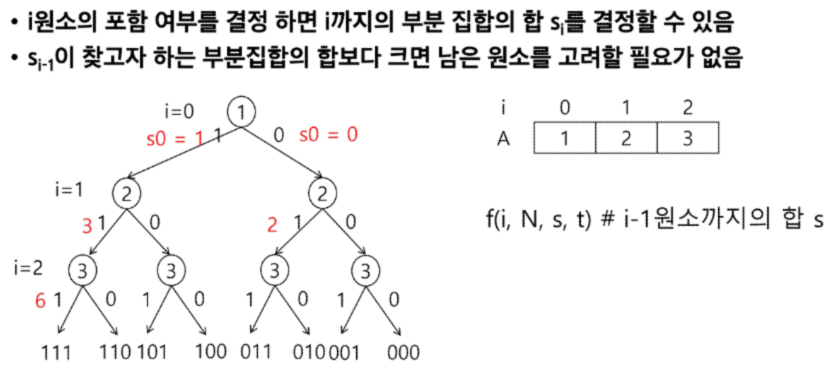
부분집합의 포함여부와 부분집합의 합 구하기

def f(i, k, s, t): # k 개의 원소를 가진 배열A, 부분집합의 합이 t인 경우
global cnt
cnt += 1
if s == t: # 목표치에 도달하면
for j in range(k):
if bit[j]: # A[i]가 포함된 경우
s += A[j]
print(A[j], end=' ')
print()
elif i == k: # 모든 원소를 고려했으나 s!=t
return
elif s > t: # 고려한 원소의 합이 t보다 큰 경우
return
else:
# for j in range(1, -1, -1):
# bit[i] = j
# f(i+1, k, t)
bit[i] = 1
f(i+1, k, s+A[i], t)
bit[i] = 0
f(i+1, k, s, t)
N = 10
A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
bit = [0] * N # bit[i]는 A[i]가 부분집합에 포함되는지 표시
cnt = 0
f(0, N, 0, 10) #처음, 끝, 합의 초깃값, 문자의 갯수
print('cnt : ', cnt) # 전부 확인하는 경우의 수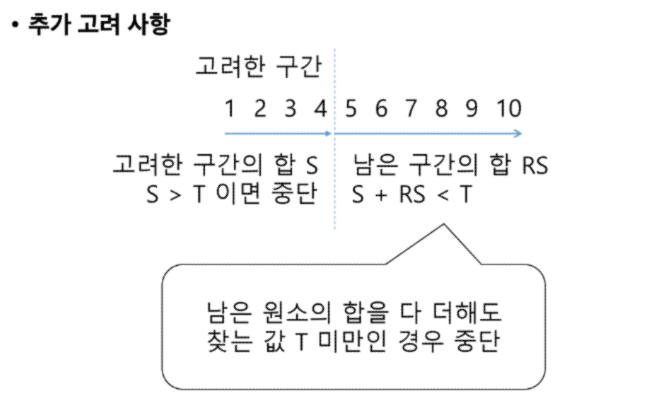
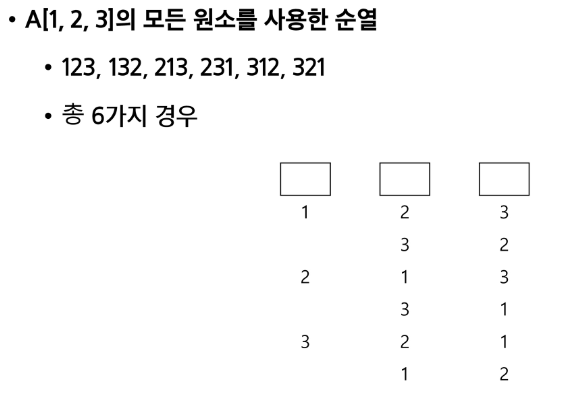
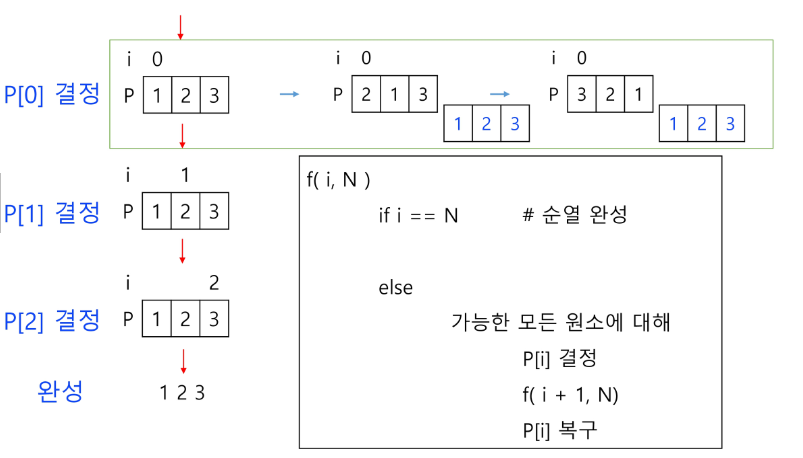
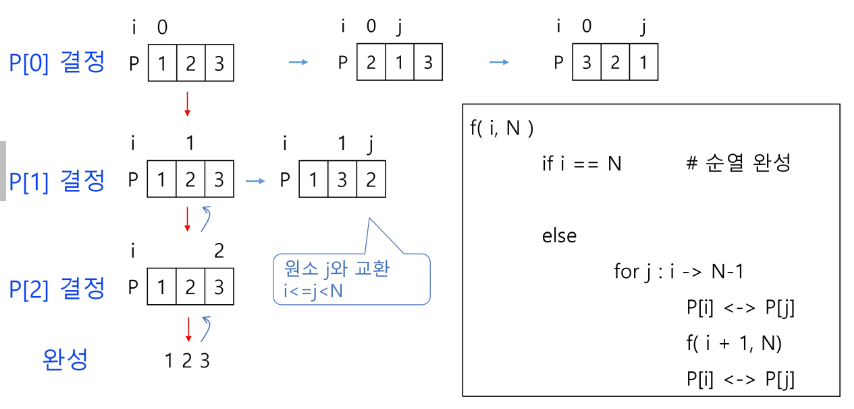
순열
def f(i, k):
if i == k:
print(*P)
else:
for j in range(i, k): # P[i] 자리에 바꿀 원소
P[i], P[j] = P[j], P[i] # P[i] <-> P[j]
f(i+1, k) # 순열 자리 결정
P[i], P[j] = P[j], P[i] # 교환전으로 복구 원상복구
N = 3
P = [1, 2, 3]
f(0, N)순열 연습문제
def f(i, k):
global min_v
global cnt
cnt += 2
if i == k:
# print(*P)
s = 0 # 선택한 원소의 합
for j in range(k): # j 행에 대해
s += arr[j][P[j]] # j 행에서 P[j]열을 고른 경우의 합 구하기
if min_v > s: # 비교하는 순서, 대입하는 순서 맞춰주면 좋음!
min_v = s
else:
for j in range(i, k): # P[i] 자리에 바꿀 원소
P[i], P[j] = P[j], P[i] # P[i] <-> P[j]
f(i+1, k) # 순열 자리 결정
P[i], P[j] = P[j], P[i] # 교환전으로 복구 원상복구
N = int(input())
arr = [list(map(int, input().split())) for _ in range(N)]
P = [i for i in range(N)]
min_v = 100 # 나와있는 모든 수를 더해도 100이 넘지 않음
cnt = 0
f(0, N)
print(min_v, cnt)def f(i, k, s): # s는 i-1까지 탐색한 합
global min_v
global cnt
cnt += 2
if i == k: # 모든 원소를 고려했니?
# print(*P)
if min_v > s: # 비교하는 순서, 대입하는 순서 맞춰주면 좋음!
min_v = s
elif s >= min_v: # 모든 원소를 고려하지 않았으면 리턴하렴
return
else:
for j in range(i, k): # P[i] 자리에 바꿀 원소
P[i], P[j] = P[j], P[i] # P[i] <-> P[j]
f(i+1, k, s+arr[i][P[i]]) # 순열 자리 결정
P[i], P[j] = P[j], P[i] # 교환전으로 복구 원상복구
N = int(input())
arr = [list(map(int, input().split())) for _ in range(N)]
P = [i for i in range(N)]
min_v = 100 # 나와있는 모든 수를 더해도 100이 넘지 않음
cnt = 0
f(0, N, 0)
print(min_v, cnt)가지치기의 효과는 입력이 많을수록 눈에 띈다! 최악의 경우 모든 경우의 수를 고려할 수도 있지만, 대부분 효과가 있다! 빽트래킹을 중요시 하라 = 가지치기 효과가 좋다
