반복과 재귀
반복과 재귀
반복과 재귀는 유사한 작업을 수행할 수 있다.
반복은 수행하는 작업이 완료될 때 까지 계속 반복
-
루프 (for, while 구조)
-
반복문은 코드를 n번 반복시킬 수 있다.
재귀는 주어진 문제의 해를 구하기 위해 동일하면서 더 작은 문제 해결 방법
-
하나의 큰 문제를 해결할 수 있는 (해결하기 쉬운) 더 작은 문제로 쪼개고 결과들을 결합한다.
-
재귀 함수로 구현
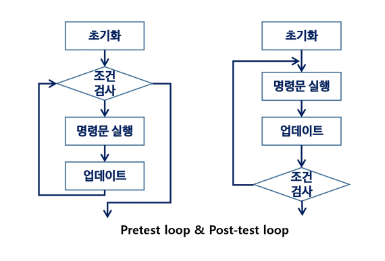
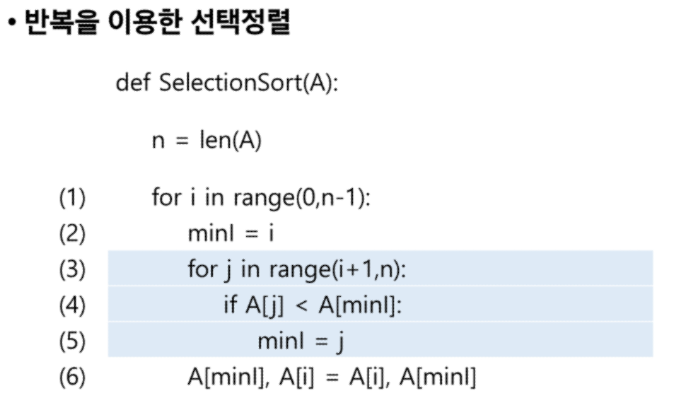
반복구조
초기화
- 반복되는 명령문을 실행하기 전에 (한번만) 조건 검사에 사용할 변수의 초기값 설정
조건 검사 (check control expression)
반복할 명령문 실행 (action)
업데이트 (loop update)
- 무한 루프 (infinite loop)가 되지 않게 조건이 거짓(false)이 되게 한다.
재귀적 알고리즘
재귀적 정의는 두 부분으로 나뉜다.
하나 또는 그 이상의 기본 경우 (basis case or rule)
- 집합에 포함되어 있는 원소로 induction 을 생성하기 위한 시드 역할
하나 또는 그 이상의 유도된 경우 (inductive case or rule)
- 새로운 집합의 원소를 생성하기 위해 결합되어지는 방법
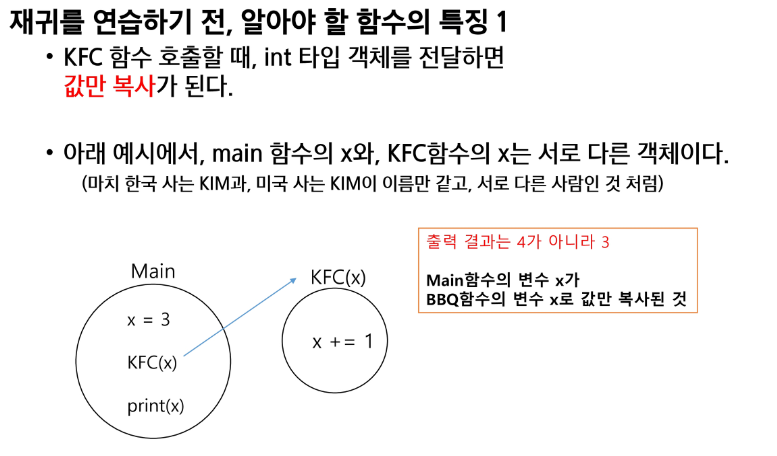
재귀를 연습하기 전, 알아야 할 함수의 특징
함수를 호출할 때, int 타입 객체를 전달하면 값만 복사한다.
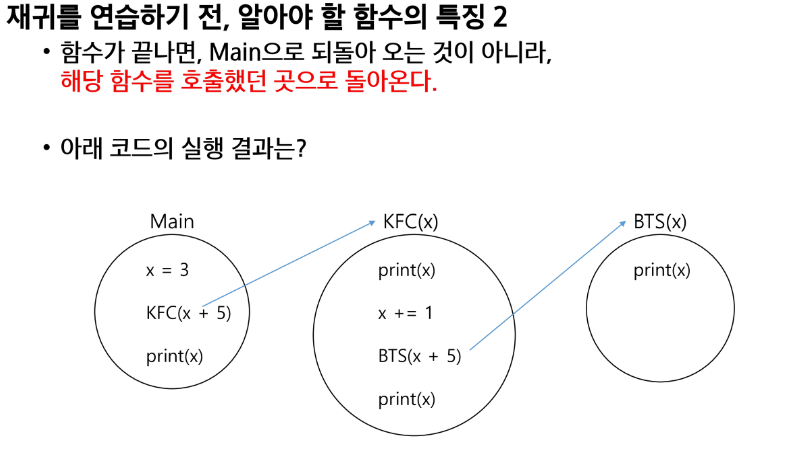
함수가 끝나면 Main으로 되돌아오는 것이 아니라 해당 함수를 호출했던 곳으로 돌아온다.
재귀 함수 (recursive function)
함수 내부에서 직접 혹은 간접적으로 자기 자신을 호출하는 함수
일반적으로 재귀적 정의를 이용해서 재귀 함수를 구현한다.
따라서 기본 부분 (basis part) 와 유도부분 (inductive part)로 구성된다.
재귀적 프로그램을 작성하는 것은 반복구조에 비해 간결하고 이해하기 쉽다.
- 그러나, 재귀에 대해 익숙하지 않은 개발자들은 재귀적 프로그램이 더 어렵다고 느낀다.
함수 호출은 프로그램 메모리 구조에서 스택을 사용한다. 따라서 재귀 호출은 반복적인 스택의 사용을 의미하며 메모리 및 속도에서 성능저하가 발생한다.



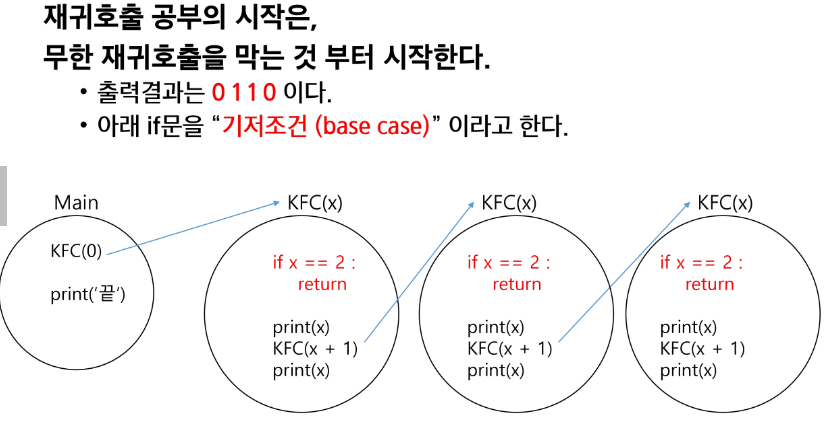

def KFC(x):
if x == 6:
return
print(x, end = ' ')
KFC(x+1)
print(x, end = ' ')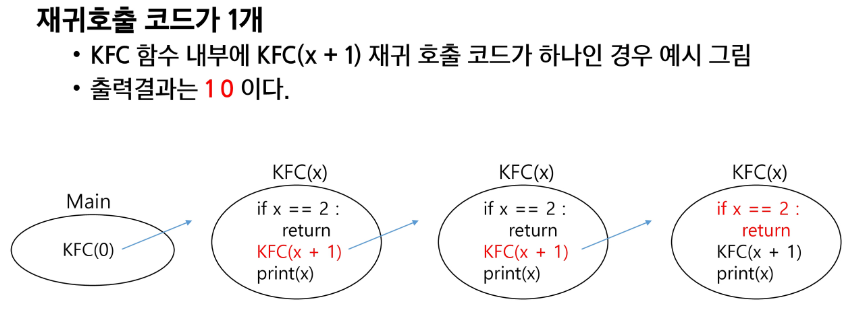
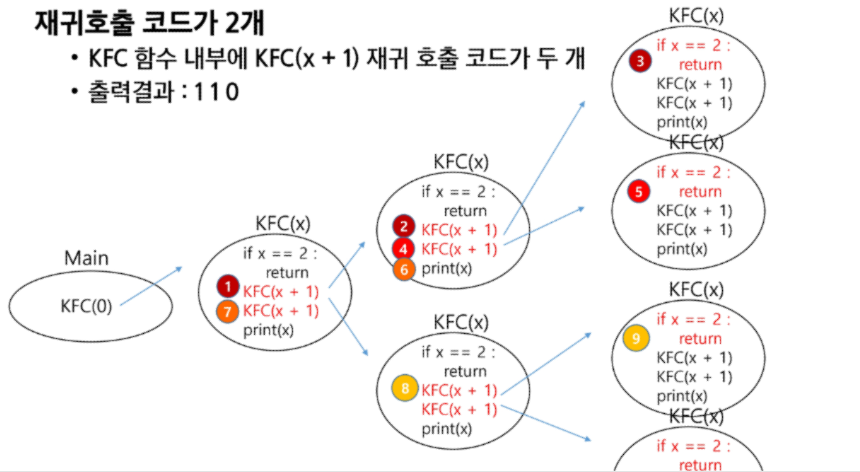
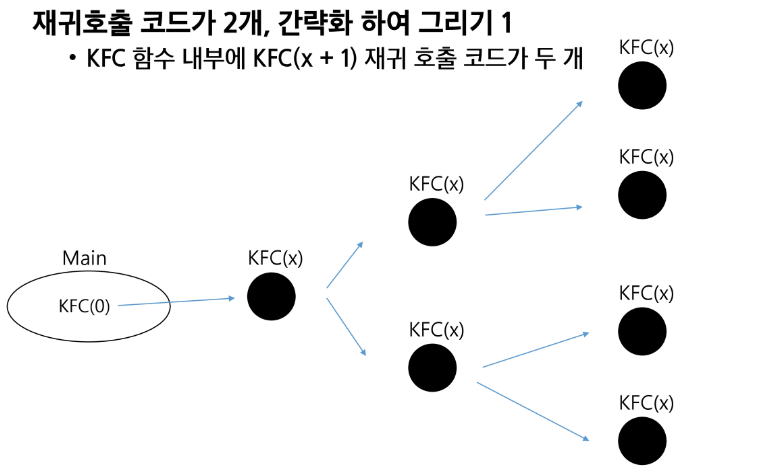
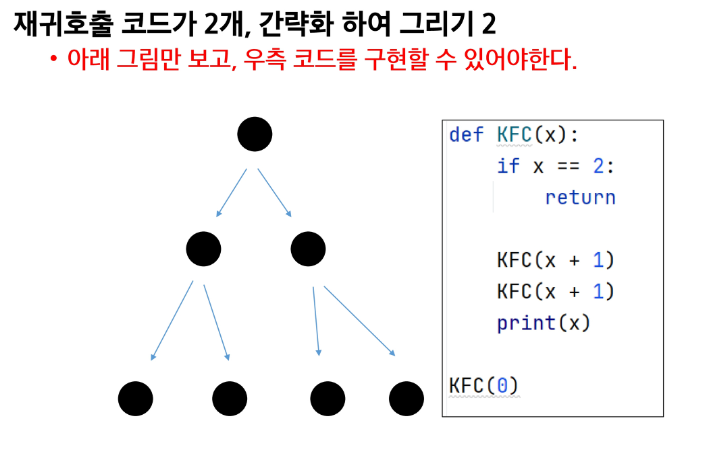
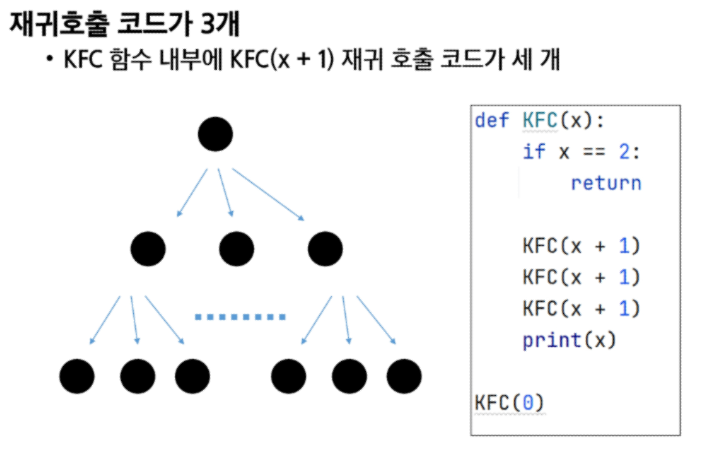
재귀가 3개 -> 가지가 3개 기저조건 3 -> level 2
재귀가 4개 -> 가지가 4개 기저조건 4 -> level 3


def run(level):
if level == 3:
return
for i in range(2):
run(level + 1)
run(0)순열
순열
서로 다른 N개에서 R개를 중복없이 순서를 고려하여 나열하는 것
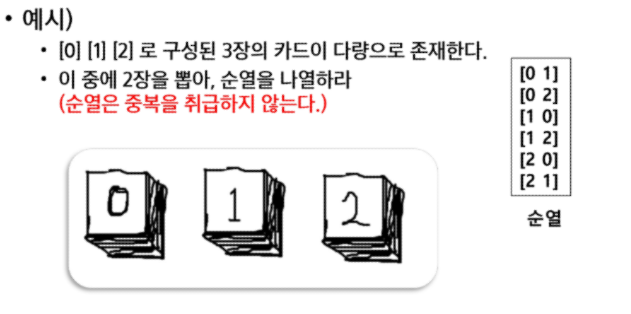
중복 순열
서로 다른 N개에서 R개를 중복을 허용하고 순서를 고려하여 나열한 것
중복 순열 구현 원리
1. 재귀호출을 할 때마다 이동 경로를 흔적으로 남긴다.
- 가장 마지막 레벨에 도착했을 때, 이동 경로를 출력한다.
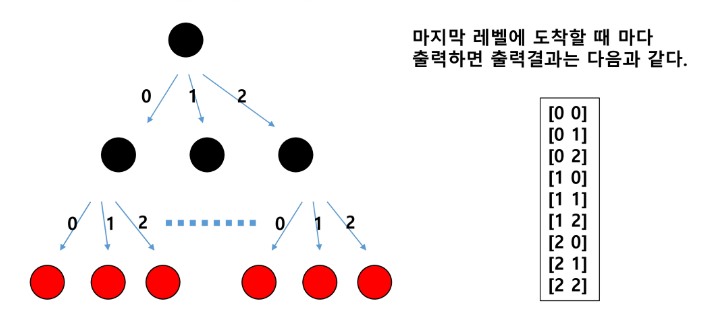
흔적 = path
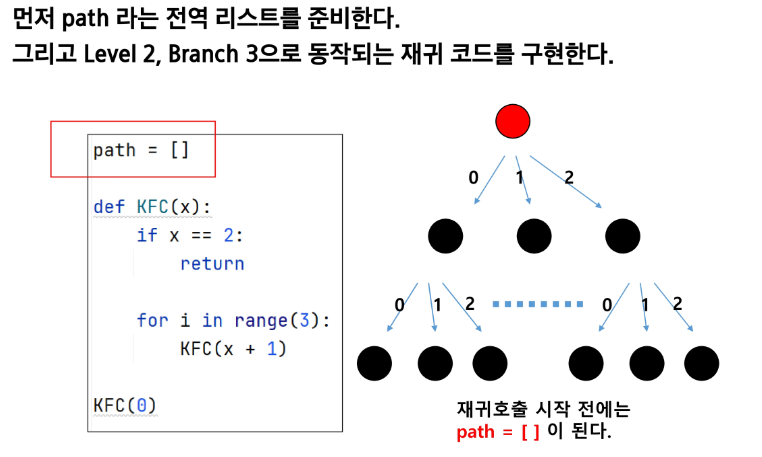
중복순열 코드
path = []
def KFC(x):
if x == 2:
print(path)
return
for i in range(3):
path.append(i)
KFC(x+1)
path.pop()
KFC(0)
print()
path = []
branch = 6
level = 3
def KFC(x):
if x == 3:
print(path)
return
for i in range(1, 7):
path.append(i)
KFC(x+1)
path.pop()
KFC(0)
print()중복을 취급하지 않는 '순열' 구현하는 방법
-
중복 순열 코드를 작성한다.
-
중복을 제거하는 코드를 추가하면 순열 코드가 된다.
중복 제거 원리
전역 리스트를 사용하면 이미 선택했던 숫자인지 아닌지 구분할 수 있다.
이를 used 배열 또는 visited 배열이라고 한다.
중복 제거 예시
0을 선택하고 재귀호출 한 후에는, 또 다시 0을 선택하지 못하도록 막아야 한다.
재귀 호출을 하기 직전, 이미 선택했던 숫자인지 아닌지 검사하는 코드가 필요하다.
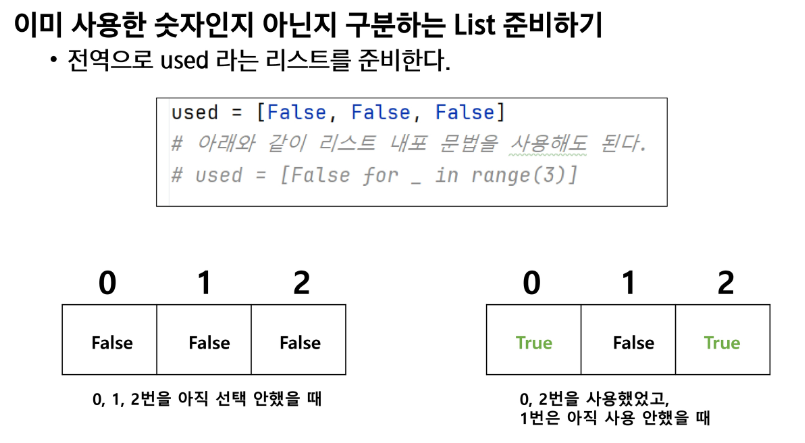
branch의 개수만큼 used를 초기화 한다.


순열
중복 순열에서 4개의 코드를 추가하면 순열이 됨
path = []
used = [False for _ in range(7)]
def KFC(x):
if x == 2:
print(path)
return
for i in range(1, 7):
if used[i] == True : continue
used[i] = True
path.append(i)
KFC(x+1)
path.pop()
used[i] = False
KFC(0)
print()
# 중복 순열
path = []
def Type_1(x):
if x == N:
print(path)
return
for i in range(1, 7):
path.append(i)
Type_1(x+1)
path.pop()
# Type_1(0)
# print()
# 순열
path = []
used = [False for _ in range(7)]
def Type_2(x):
if x == N: # level의 갯수
print(path)
return
for i in range(1, 7): # 구하고자 하는 숫자의 범위
if used[i] == True : continue
used[i] = True
path.append(i)
Type_2(x+1)
path.pop()
used[i] = False
# Type_2(0)
# print()
N, Type = map(int, input().split()) # N 기저조건
if Type == 1:
Type_1(0)
else:
Type_2(0)
print()
완전탐색
완전탐색 (= Brute-Force, 부르트 포스 알고리즘 이라고 한다.)
모든 가능한 경우를 시도해 정답을 찾아내는 알고리즘
완전 탐색 예시


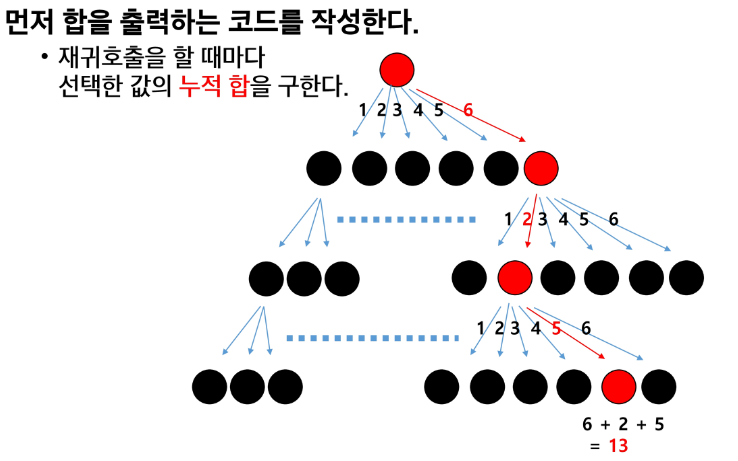


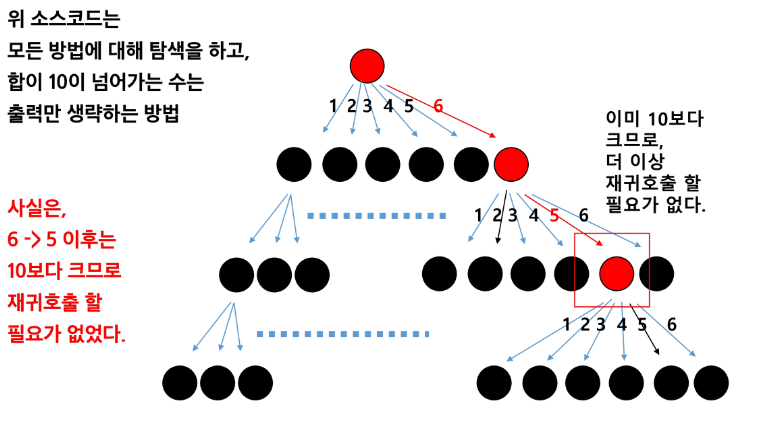

이미 숫자가 10을 넘은 경우 가지치기를 해서 불필요한 재귀호출을 하지 않는다. = 백트래킹
path = []
def Type_1(x, sum):
if sum > 10: # 가지치기 불필요한 과정 제거! 런 타임 줄일 수 있음
return
if x == 3:
if sum <= 10:
print(f'{path} = {sum}') # 출력
return
for i in range(1, 7):
path.append(i)
Type_1(x+1, sum + i)
path.pop()
Type_1(0, 0)
print()
