Notion에서 작성한 글이라, 여기 에서 더 깔끔하게 보실 수 있습니다! 😮🥹
[Beginner] 올바른 괄호
Solution.
def solution(s):
stack = []
for c in s:
if c == '(':
stack.append(c)
else:
if stack:
stack.pop()
else:
return False
return not stack- 전형적인 스택 문제이다.
stack에 원소가 없을 때pop()하게 되면 IndexError가 발생하기 때문에, 이처럼if stack으로 체크한 다음pop()하는 방법이 있고,try-except를 이용하는 방법도 있다. - 괄호의 종류가 중요하지 않기 때문에,
stack에 굳이(를 push할 필요가 없긴 하다.- Integer 변수를 이용하여
append()할 때 1을 더하고,pop()할 때 1을 빼주고, 마지막에 그 값이 0인지 아닌지만 체크해주면 된다.- 이 때 주의할 점은,
)()(와 같은 입력이 주어졌을 때[2]를 지나고 -1이 되었다가,[3]에서 다시 0이 되어 마치 올바른 괄호 쌍처럼 보이기 때문에, 해당 변수가 음수가 될 때False를 return하는 식으로 작성하여야 한다.
- 이 때 주의할 점은,
- Integer 변수를 이용하여
[Middler] 기능개발
Solution 1.
from collections import deque
def solution(progresses, speeds):
answer = []
progresses = deque(progresses)
speeds = deque(speeds)
while progresses:
pop_cnt = 0
while progresses[0] < 100:
# progresses = deque(x+y for x,y in zip(progresses, speeds))
for i in range(len(progresses)):
progresses[i] += speeds[i]
while progresses and progresses[0] >= 100:
progresses.popleft()
speeds.popleft()
pop_cnt += 1
answer.append(pop_cnt)
return answer- 가장 단순하게 구현한 풀이이다. 하루에 진행되는 작업만큼 계속해서 작업현황을 갱신해준다. 그러던 중 첫 번째 기능이 100% 완료되면, 100% 완료되지 않은 작업이 나올 때까지
popleft()하면서 배포한 개수를 세어준다. - 작업의 현황을 업데이트할 때,
zip()을 이용하는 것이 더 깔끔해보이나 deque로 다시 바꿔주는 과정에서 추가적인 시간이 소모되기 때문에 인덱스로 접근했다.
Solution 2.
from collections import deque
def solution(progresses, speeds):
answer = []
progresses = deque(progresses)
speeds = deque(speeds)
t = 1
pop_cnt = 0
while progresses:
if progresses[0] + speeds[0]*t >= 100:
progresses.popleft()
speeds.popleft()
pop_cnt += 1
else:
if pop_cnt:
answer.append(pop_cnt)
pop_cnt = 0
t += 1
answer.append(pop_cnt)
return answer- Solution 1. 에서, 굳이 매일매일 모든 작업현황을 갱신해줘야하는가? 에 대해 생각해 보았다.
- 중요한 것은 아직 배포되지 않은 첫 번째 작업의 진도이기 때문에, 작업일수를 의미하는 변수
time을 이용하여, 이를 증가시켜가며 첫 번째 작업의 진행상황만을 체크한다. - 이 방법을 이용하면 매일 모든 작업현황을 갱신해줄 필요가 없어지기 때문에, 선형 시간에 해결이 가능해진다.
- 중요한 것은 아직 배포되지 않은 첫 번째 작업의 진도이기 때문에, 작업일수를 의미하는 변수
- 이 방법의 시간복잡도에 대해 생각해 보자. 첫 번째 작업의 진도가 1, 개발속도가 1일 때를 가정하면 작업의 개수가 한 개여도
t를 증가시키느라whileloop는 99회 반복된다. 여기에, 작업의 수까지 더해져 회 반복된다.
Solution 2-2.
def solution(progresses, speeds):
answer = []
t = 1
pop_cnt = 0
i = 0
while i < len(progresses):
if progresses[i] + speeds[i]*t >= 100:
i += 1
pop_cnt += 1
else:
if pop_cnt:
answer.append(pop_cnt)
pop_cnt = 0
t += 1
answer.append(pop_cnt)
return answer- Solution 2. 에서,
progress와speeds에서popleft()한 정보는 의미를 갖지 않는다. 게다가 리스트로 입력받은 이 둘을deque로 바꿔주는 과정에서 각각 의 시간이 소요되기 때문에,deque를 이용하지 않고 단순히 인덱스로 접근함으로써 계수를 커팅할 수 있다.
Solution 3.
from math import ceil
def solution(progresses, speeds):
answer = []
t = [ceil((100-p)/s) for p, s in zip(progresses, speeds)]
mx = t[0]
cnt = 1
for i in range(1, len(t)):
if t[i] <= mx:
cnt += 1
else:
answer.append(cnt)
mx = t[i]
cnt = 1
answer.append(cnt)
return answer- Solution 2. 에서, 굳이 작업일을 1씩 늘려가면서 비교해야하는가? 에 대해 생각해 보았다.
- 남은 작업 진도를 계산해놓고, 각 작업에 대해 며칠이 지나면 작업이 완료되는지를 에 계산해 놓은 다음 개수를 세어 주면 더 빠른 시간에 해결할 수 있다.
- 여기서 올림에 해당하는
ceil()을 해주는 이유는, 배포가 하루의 끝에 이루어지기 때문이다.- 예를 들어 생각해 보자. 작업 진도가 5%p 남았고, 하루에 4%p의 작업을 하면, 1.25일 후에 배포를 하는 것이 아닌 2일 후에 배포를 하는 것이다.
Solution 3-2.
from math import ceil
def solution(progresses, speeds):
answer = []
cnt = 0
mx = ceil((100-progresses[0])/speeds[0])
for p, s in zip(progresses, speeds):
cur = ceil((100-p)/s)
if cur <= mx:
cnt += 1
else:
answer.append(cnt)
mx = cur
cnt = 1
answer.append(cnt)
return answer- 굳이 리스트를 만들어 놓고 세어주어야 하는가? 에 대해 생각해 보았다. 작업이 완료되기까지 걸리는 시간을 계산하는 과정에서, 각 배포마다 몇 개의 기능이 배포되는지까지 한 번에 세어 줄 수 있다.
- 따로 리스트를 생성하지 않기에 메모리 사용도 더 적고, 최종적으로 계수가 없는 으로 해결할 수 있게 된다. 시간복잡도상 이보다 빠른 코드는 없을 거라는 생각이 들었다.
[Challenger] 두 큐 합 같게 만들기
queue1,queue2를 각각 , 라 하자. 두 큐의 합을 같게 만든다는 것은,- 를 만족해야 한다.
- 하지만 이 값이 홀수일 경우, 어떠한 경우에도 두 큐의 합을 같게 만들 수 없으므로
-1을 return해주면 된다.
- 매번 를 비교하며, 가 큰 queue에서
popleft()한 다음, 작은 queue에append()해주는 과정을 반복한다.- 언제까지?
- 난 이 부분에서 틀렸었다. 내 생각은, 둘 다 queue의 size만큼
popleft(),append()하고 나면 서로 swap된 형태가 되므로 이 때부턴 더이상 작업하는 것이 의미가 없을 것이라고 판단했다. → WACounterExample
Input:
[1, 1, 1, 1], [1, 1, 7, 1]Expected:
9 - Circular Queue의 형태를 떠올리면 아주아주아주 직관적이다.
- 그림과 함께 설명해야 좋은데,,, 하나하나 만들 시간이 당장 부족해서 풀 때 끄적거린 페이지를 첨부하겠다,,,!!
끄적끄적 적은 거라,,, 글씨는 양해해주셨으면,,, 😓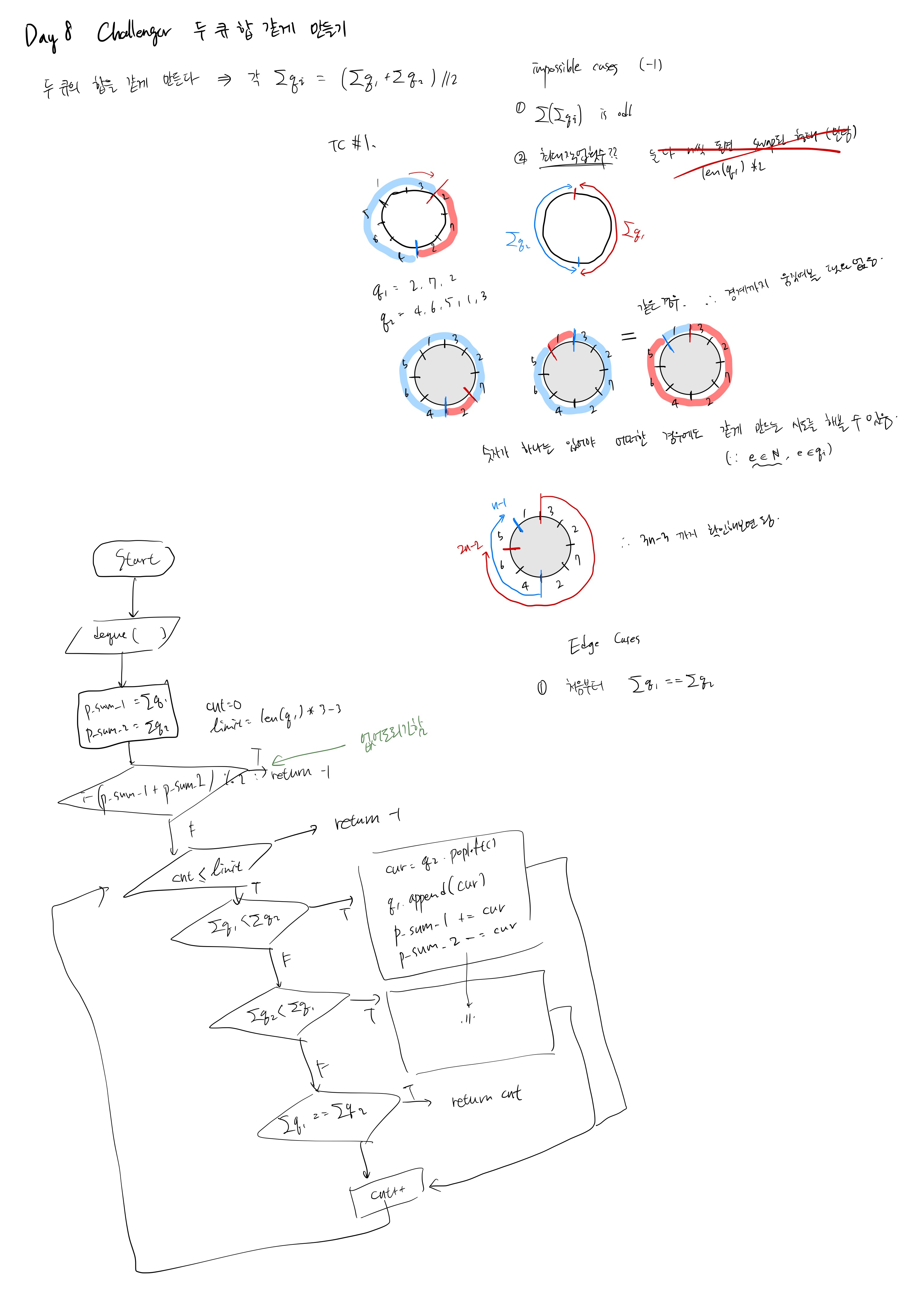
- 그림과 함께 설명해야 좋은데,,, 하나하나 만들 시간이 당장 부족해서 풀 때 끄적거린 페이지를 첨부하겠다,,,!!
- 난 이 부분에서 틀렸었다. 내 생각은, 둘 다 queue의 size만큼
- 언제까지?
- 한 가지 더 생각해볼 point가 있다. 매번 를
sum()과 같이 에 확인하면 무조건 TLE가 난다. 한 번의 작업에서 어떤 queue에서 pop되면 다른 queue에 append된다는 점에 주목하여, Prefix Sum이나 Sliding Window와 비슷한 느낌으로 매 작업마다 에 처리해주면 된다.
Solution 1. Queue
from collections import deque
def solution(queue1, queue2):
queue1 = deque(queue1)
queue2 = deque(queue2)
psum1 = sum(queue1)
psum2 = sum(queue2)
if (psum1+psum2)%2: return -1
limit = len(queue1)*3-3
cnt = 0
while cnt <= limit:
if psum1 < psum2:
cur = queue2.popleft()
queue1.append(cur)
psum1 += cur
psum2 -= cur
elif psum2 < psum1:
cur = queue1.popleft()
queue2.append(cur)
psum2 += cur
psum1 -= cur
else: return cnt
cnt += 1
return -1Solution 2. Two Pointer
def solution(queue1, queue2):
merged_queue = queue1 + queue2
psum1 = sum(queue1)
psum2 = sum(queue2)
if (psum1+psum2)%2: return -1
cnt = 0
l, r = 0, len(queue1)
while l<r and r<len(merged_queue):
if psum1 < psum2:
psum1 += merged_queue[r]
psum2 -= merged_queue[r]
r += 1
elif psum2 < psum1:
psum1 -= merged_queue[l]
psum2 += merged_queue[l]
l += 1
else: return cnt
cnt += 1
return -1- Two pointer를 이용한 방식이다. 아이디어는 Circular Queue에서 비롯됐다. 두 큐를 이어붙여놓은 상태를 상상해 보자. 이 상태로 합의 기준이 되는
l,r을 조정해가며 기존 방식과 매우 유사하게 풀 수 있다. 이를 통해 더 직관적으로 최대 번까지만 체크해주면 된다는 것을 확인할 수 있다.
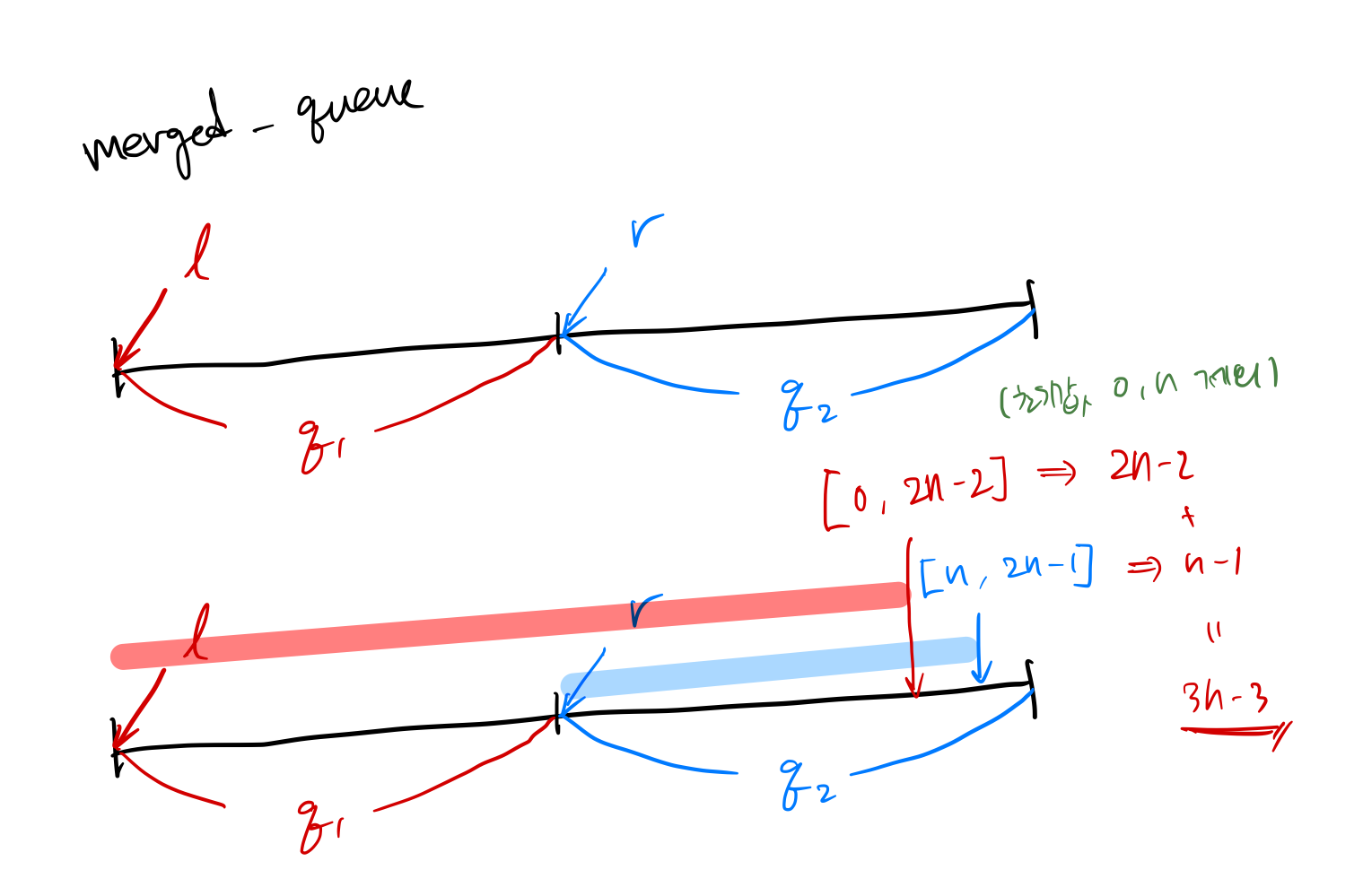
r이 밖으로 나가는 경우는 곧 불가능한 케이스를 의미한다.r이 인덱스 범위 밖으로 나가는 경우에 유의해야 한다.
Memo
Middler
math.ceil()없이 올림 구현해봐야 겠다.
Challenger Solution 2.
- 생각을 좀 더 해봤는데, 위 코드에서 target을 따로 저장해놓는다면
psum1,psum2중 하나는 갱신해주지 않아도 될 것 같다. 이 방법으로 상수커팅을 좀 해볼 수 있겠고, merged_queue를 위와 같이 만들면 의 시간이 소요되는데, 어차피 이후에 각각의 큐를 분리해서 생각할 필요가 없어지므로extend()로 에 처리하면서 계수커팅을 해볼 수 있겠다.- 또는, 아예 각 큐를 합치지도, 확장하지도 않고 마치 두 큐가 이어져있는 것처럼
l이 구간에 존재할 땐queue2를 참조하는 식으로 합치는 데 드는 시간을 아예 소모하지 않도록 바꿀 수 있어보인다. 요새 시간이 너무너무 없어서... 나중에 더 타이트하게 쥐어짜봐야 겠다.